يمكن الحصول على الخصائص الديناميكية للحركة الأرضية من خلال تسجيلات السيسموغراف (محطة رصد الزلازل). يمكن تمثيل تابع البؤرة والأمواج الصادرة عن التمزق على سطح الفالق من خلال ثني تابع العزم الزلزالي مع التابع المعبر عن الزمن الذي يستغرقه التمزق، ويمكن تمثيل التابعين السابقين بتابعين مربعي الشكل ينتج عن ثنيهما تابع له شكل شبه منحرف وهو تابع البؤرة Source time function.
إن تحويل فورييه للتابع الناتج هو عبارة عن جداء تحويل فورييه لكلا التابعين السابقين.، حيث أن تحويل فورييه لتابع قيمته 1/T وطوله T هو الشكل(1).
ملاحظة: التابع الذي طوله الزمني T وقيمته 1/T هو تابع مساحته تساوي واحدة المساحة.
بنفس الطريقة يمكن تمثيل طيف السعة لتابع البؤرة من خلال العلاقة في الشكل(2).
حيث أن TR و TD هما زمن التمزق الكلي وزمن التمزق النقطي على سطح الفالق على الترتيب الشكل(3).
بأخذ لوغاريتم الطرفين الشكل(4)
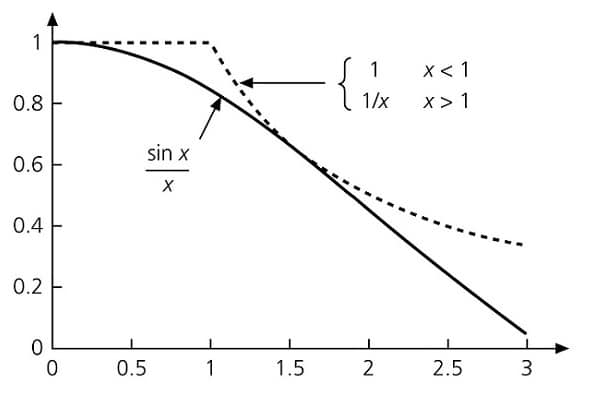
يمكن تقريب التابع sinc x كما يلي الشكل(5)
Sinc x = Sin x/x = 1/x (x>1)
Sinc x = 1 (x<1)
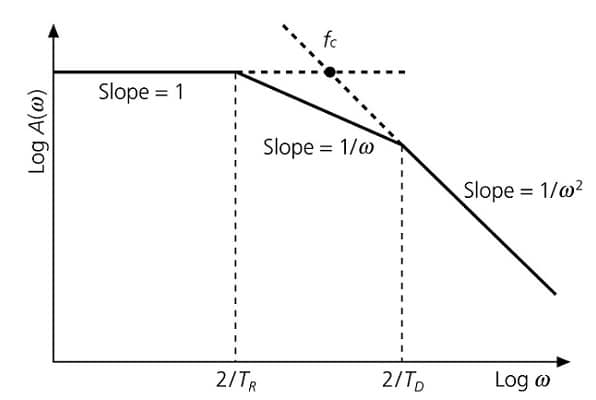
التابع log |A(w)| مقابل log w الشكل(6) يتألف في هذه الحالة من ثلاثة أجزاء الشكل(7).
وبالتالي يتألف منحني الطيف السابق من ثلاثة أجزاء مقسمة بواسطة الترددات: 2/TR و 2/TD والتي تسمى الترددات الزاوية، ويكون الطيف مسطحا من أجل الترددات الزاوية الأقل من 2/TR، في حين يصبح ميل منحني الطيف w-¹ بين الترددين الزاويين 2/TR و 2/TD وأخيرا من أجل الترددات العالية يصبح الميل w-²، وبذلك يمكن توصيف طيف البؤرة من خلال ثلاثة بارامترات هي العزم الزلزالي، وزمن إتمام التمزق النقطي وزمن إتمام كامل التمزق على سطح الفالق.
هناك بعض الموديلات الفالقية التي يدخل فيها بارامتر رابع يعبر عن عرض الفالق ويظهر في طيف البؤرة على شكل جزء ميله w-³ عند الترددات العالية وموديلات أخرى لها بالمقابل تردد زاوي وحيد يدمج تأثير كل من الزمنين TR وTD.
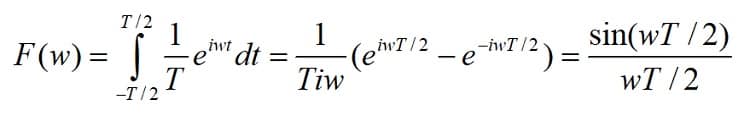
الشكل(1)

الشكل(2)

الشكل(3)

الشكل(4)
الشكل(5)
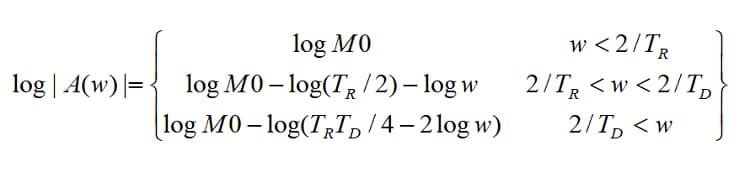
الشكل(6)
الشكل(7)
