التميع

إن التميع هو أحد أهم المواضيع وأكثرها إثارة للاهتمام وتعقيدا وإثارة للجدل في مجال هندسة الزلازل الجيوتقنية. وقد لفتت تأثيراته المدمرة انتباه المهندسين الجيوتقنيين في فترة ثلاثة أشهر في عام 1964 عندما أعقب زلزال الجمعة العظيمة (Mw = 9.2) في ألاسكا زلزال نيغاتا (Ms = 7.5) في اليابان. وقد أحدث الزلزالان أمثلة مذهلة على الأضرار الناجمة عن التميع، بما في ذلك انهيار المنحدرات، وانهيار أساسات الجسور والمباني، وتعويم الهياكل المدفونة. وعلى مدى الثلاثين عاما التي مرت منذ وقوع هذين الزلزالين، درس مئات الباحثين في جميع أنحاء العالم التميع على نطاق واسع. وقد تعلمنا الكثير، لكن الطريق لم يكن ممهدا. فقد تم اقتراح مصطلحات وإجراءات وطرق تحليل مختلفة، وكان النهج السائد بطيئا في الظهور. وفي السنوات الأخيرة، تم التوفيق بين العديد من هذه الاختلافات من خلال إدراك أن أسبابها كانت ترجع، إلى حد كبير، إلى الدلالات. لقد تم استخداممصطلح التميع لوصف عدد من الظواهر المختلفة، وإن كانت مترابطة. وبدلا من محاولة تتبع التطور المعقد للحالة الحالية للمعرفة فيما يتعلق بالتميع، سنقدم إطارا أساسيا للفهم المفاهيمي لسلوك التربة المرتبط بالتميع واستخدامه لوصف الطرق المختلفة التي يمكن من خلالها تقييم مخاطر التميع. للقيام بذلك، نقدم بعض المصطلحات الجديدة للتمييز بين الظواهر التي تم تجميعها بشكل متكرر تحت عنوان التميع. تسمح المصطلحات الجديدة بتوضيح هذه الظواهر بطريقة تبسط فهم آلياتها والطريقة التي تساهم بها في أضرار الزلازل.

الظواهر المرتبطة بالتميع

لقد استخدم مصطلح التميع، الذي صاغه في الأصل Mogami and Kubo (1953)، تاريخيا بالتزامن مع مجموعة متنوعة من الظواهر التي تنطوي على تشوهات التربة الناجمة عن اضطراب رتيب أو عابر أو متكرر للتربة المشبعة عديمة التماسك في ظل ظروف غير ممطرة. إن توليد ضغط مسام زائد في ظل ظروف تحميل غير مستنزفة هو السمة المميزة لجميع ظواهر التميع. إن ميل التربة الجافة عديمة التماسك إلى التكثيف تحت كل من التحميل الساكن والدوري معروف جيدا. ومع ذلك، عندما تكون التربة عديمة التماسك مشبعة، يحدث تحميل سريع في ظل ظروف غير مستنزفة، وبالتالي فإن ميل التكثيف يتسبب في زيادة ضغوط المسام الزائدة وتقليل الضغوط الفعالة. يمكن تقسيم ظواهر التميع الناتجة عن هذه العملية إلى مجموعتين رئيسيتين: التميع التدفقي والحركة الدورية. إن كلاً من التميع التدفقي والحركة الدورية مهمان للغاية، وأي تقييم لمخاطر التميع يجب أن يأخذ كليهما في الاعتبار بعناية. في الميدان، يحدث التميع التدفقي بشكل أقل تكرارا من الحركة الدورية ولكن آثاره عادة ما تكون أكثر شدة. من ناحية أخرى، يمكن أن تحدث الحركة الدورية في ظل نطاق أوسع بكثير من ظروف التربة والموقع مقارنة بالتميع التدفقي؛ يمكن أن تتراوح آثاره من غير ذات أهمية إلى شديدة الضرر. سيتم أخذ المصطلح العام للتميع ليشمل كلاً من التميع التدفقي والحركة الدورية. سيتم تحديد التميع التدفقي والحركة الدورية بشكل فردي عند الضرورة.

– التميع التدفقي:

ينتج التميع التدفقي التأثيرات الأكثر دراماتيكية من بين جميع الظواهر المرتبطة بالتميع كعدم الاستقرار الهائل المعروف باسم فشل التدفق. يمكن أن يحدث التميع التدفقي عندما يكون إجهاد القص المطلوب لتحقيق التوازن الساكن لكتلة التربة (إجهاد القص الساكن) أكبر من قوة قص التربة في حالتها المسالة. وبمجرد حدوث التشوهات الكبيرة الناتجة عن التميع التدفقي، فإنها في الواقع مدفوعة بإجهادات القص الساكنة. وقد تؤدي الإجهادات الدورية ببساطة إلى جلب التربة إلى حالة غير مستقرة حيث تنخفض قوتها بشكل كافٍ للسماح للإجهادات الساكنة بإنتاج فشل التدفق. تتميز فشلات التميع التدفقي بطبيعة منشأها المفاجئة، والسرعة التي تتطور بها، والمسافة الكبيرة التي تتحرك بها المواد المسالة غالبا. فشل التميع التدفقي لسد شيفيلد (الشكل 1.5) وسد سان فرناندو السفلي (الشكل 1.7) من أمثلة التميع التدفقي. يتم توضيح الطبيعة السائلة للتربة المسالة في (الشكل 9.1).

الشكل(1.5)

الشكل(1.7)

الشكل(9.1)

– الحركة الدورية:

الحركة الدورية هي ظاهرة أخرى يمكن أن تنتج أيضًا تشوهات دائمة كبيرة وغير مقبولة أثناء اهتزاز الزلزال. وعلى النقيض من التميع التدفقي، تحدث الحركة الدورية عندما يكون إجهاد القص الساكن أقل من قوة القص للتربة المسالة. تتطور التشوهات الناتجة عن فشل الحركة الدورية بشكل تدريجي أثناء اهتزاز الزلزال. وعلى النقيض من التميع التدفقي، فإن التشوهات الناتجة عن الحركة الدورية مدفوعة بكل من إجهادات القص الدورية والثابتة. يمكن أن تحدث هذه التشوهات، التي يطلق عليها الانتشار الجانبي، على أرض منحدرة بلطف شديد أو على أرض مستوية تقريبا بجوار المسطحات المائية (الشكل 9.2). عندما تكون الهياكل موجودة، يمكن أن يتسبب الانتشار الجانبي في أضرار كبيرة (الشكل 1.8 و1.9). هناك حالة خاصة من الحركة الدورية وهي التميع المستوي. نظرًا لعدم وجود إجهادات القص الأفقية الثابتة التي يمكن أن تؤدي إلى تشوهات جانبية، يمكن أن تنتج عملية تميع الأرض المستوية حركة كبيرة وفوضوية تعرف باسم تذبذب الأرض أثناء اهتزاز الزلزال، ولكنها تنتج حركة جانبية دائمة قليلة للتربة. تحدث حالات فشل عملية تميع الأرض المستوية بسبب التدفق الصاعد للمياه الذي يحدث عندما تتبدد ضغوط المسام الزائدة الناجمة عن الزلازل. اعتمادا على طول الوقت المطلوب للوصول إلى التوازن الهيدروليكي، قد يحدث فشل عملية تميع الأرض المستوية بعد فترة طويلة من توقف اهتزاز الأرض. يعد الهبوط الرأسي المفرط والفيضانات الناتجة عن الأراضي المنخفضة وتطور غليان الرمل (الشكل 9.3) من سمات عملية تمييع الأرض المستوية.

الشكل(9.2)

الشكل(1.8)

الشكل(1.9)

الشكل(9.3)

تقييم مخاطر التميع:

يمكن أن يؤدي كل من التميع التدفقي والحركة الدورية إلى إحداث أضرار في موقع معين، ويتطلب التقييم الكامل لمخاطر التميع معالجة احتمالات كل منهما. وعند مواجهة مثل هذه المشكلة، يمكن لمهندس الزلازل الجيوتقني تقييم مخاطر التميع المحتملة بشكل منهجي من خلال معالجة الأسئلة التالية: 1. هل التربة عرضة للتميع؟ 2. إذا كانت التربة عرضة للتميع، فهل سيتسبب ذلك في التميع؟ 3. إذا حدث التميع، فهل سيحدث ضرر؟

إذا كانت الإجابة على السؤال الأول لا، فيمكن إنهاء تقييم مخاطر التميع باستنتاج مفاده أن مخاطر التميع غير موجودة. وإذا كانت الإجابة بنعم، فيجب معالجة السؤال التالي. وفي بعض الحالات قد يكون من الأكثر كفاءة عكس ترتيب السؤالين الثاني والثالث، وخاصة عندما يبدو الضرر غير مرجح. وإذا كانت الإجابات على الأسئلة الثلاثة بنعم، فهناك مشكلة؛ إذا كان مستوى الضرر المتوقع غير مقبول، فيجب التخلي عن الموقع أو تحسينه أو تعزيز الهياكل الموجودة في الموقع. تتعلق هذه الأسئلة بالجوانب الثلاثة الأكثر أهمية في تقييم مخاطر التميع: القابلية للتأثر، والبدء، والآثار. يجب أخذ جميع هذه الجوانب الثلاثة في الاعتبار في التقييم الشامل لمخاطر التميع.

قابلية التميع:

ليست كل التربة عرضة للتميع؛ وبالتالي، فإن الخطوة الأولى في تقييم مخاطر التميع هي عادةً تقييم قابلية التميع. إذا لم تكن التربة في موقع معين قابلة للتأثر، فلن تكون مخاطر التميع موجودة ويمكن إنهاء تقييم مخاطر التميع. ومع ذلك، إذا كانت التربة قابلة للتأثر، فيجب معالجة مسائل بدء التميع وتأثيراته. هناك عدة معايير يمكن من خلالها الحكم على قابلية التميع، وبعضها يختلف بالنسبة للتميع التدفقي والحركة الدورية. وتشمل هذه المعايير المعايير التاريخية والجيولوجية والتركيبية ومعايير الحالة.

– المعايير التاريخية

لقد تم الحصول على قدر كبير من المعلومات حول سلوك التميع من خلال التحقيقات الميدانية التي أجريت بعد الزلازل، والتي أظهرت أن التميع يتكرر غالبا في نفس الموقع عندما تظل ظروف التربة والمياه الجوفية دون تغيير (Youd. 1984). وبالتالي، يمكن استخدام سجلات حالات التميع لتحديد مواقع معينة، أو ظروف أكثر عمومية للموقع، والتي قد تكون عرضة للتميع في الزلازل المستقبلية. وصف (Youd. 1991) عددا من الحالات حيث تم استخدام الأدلة التاريخية للتميع لرسم خريطة قابلية التميع. كما أظهرت التحقيقات الميدانية التي أجريت بعد الزلازل أن تأثيرات التميع كانت تقتصر تاريخيا على منطقة ضمن مسافة معينة من المصدر الزلزالي. قام (Ambraseys. 1988) بتجميع بيانات عالمية من الزلازل الضحلة لتقدير مسافة مركزية محدودة لم يتم ملاحظة التميع بعدها في الزلازل ذات الشدة المختلفة (الشكل 9.4). تزداد المسافة التي يمكن توقع حدوث التميع عندها بشكل كبير مع زيادة القدر. وفي حين لا تقدم العلاقات من النوع الموضح في الشكل 9.4 أي ضمان بعدم حدوث التميع على مسافات أكبر، إلا أنها مفيدة لتقدير سيناريوهات خطر التميع الإقليمية.

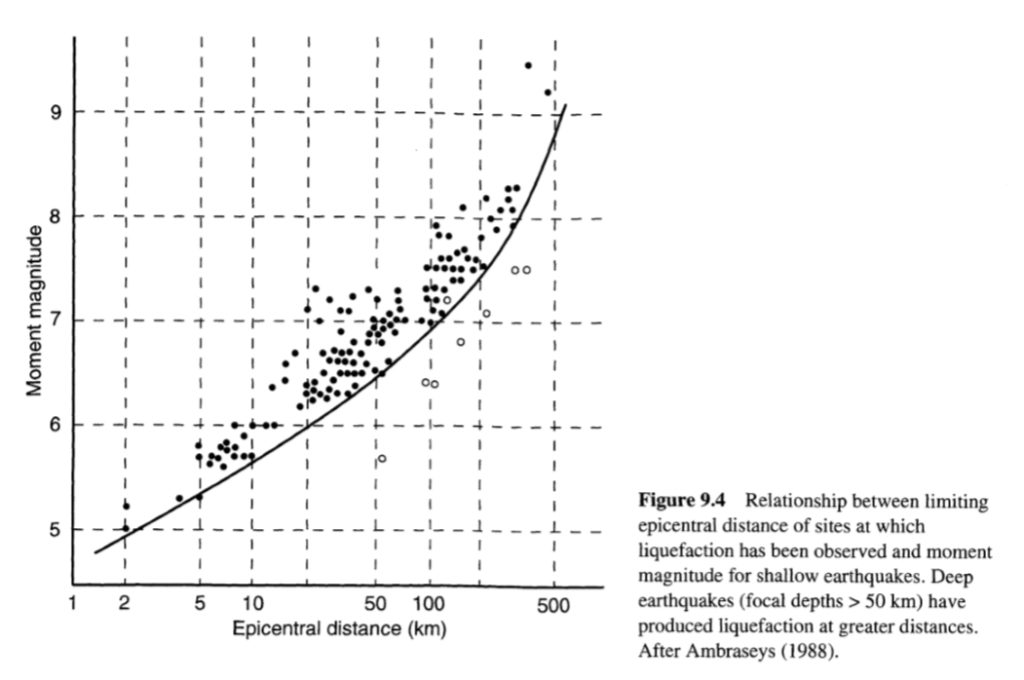
الشكل(9.4)

– المعايير الجيولوجية

تتكون رواسب التربة القابلة للتميع ضمن نطاق ضيق نسبيا من البيئات الجيولوجية (Youd, 1991). تساهم البيئة الترسيبية والبيئة الهيدرولوجية وعمر رواسب التربة في قابليتها للتميع (Youd and Hoose, 1977). تنتج العمليات الجيولوجية التي تصنف التربة إلى توزيعات موحدة لحجم الحبيبات وترسبها في حالات هشة رواسب تربة ذات قابلية عالية للتميع. وبالتالي، من المرجح أن تكون الرواسب النهرية والرواسب الرسوبية والريحية عندما تكون مشبعة عرضة للتميع. كما لوحظت عملية التميع في رواسب المروحة الرسوبية والسهول الرسوبية والشاطئ والمصب، ولكن ليس بنفس الثبات كما هو الحال في تلك المذكورة سابقا. تكون قابلية رواسب التربة القديمة للتميع أقل عموما من قابلية الرواسب الأحدث. إن التربة في العصر الهولوسيني أكثر عرضة من التربة في العصر البلستوسيني، على الرغم من أن قابلية التعرض تقل مع تقدم العمر في العصر الهولوسيني. إن تميع الرواسب التي تعود إلى ما قبل البلستوسين أمر نادر. يحدث التميع فقط في التربة المشبعة، وبالتالي فإن عمق المياه الجوفية (سواء كانت حرة أو جاثمة) يؤثر على قابلية التعرض للتميع. تقل قابلية التعرض للتميع مع زيادة عمق المياه الجوفية؛ وتلاحظ تأثيرات التميع بشكل شائع في المواقع التي تكون فيها المياه الجوفية على بعد أمتار قليلة من سطح الأرض. وفي المواقع التي تتقلب فيها مستويات المياه الجوفية بشكل كبير، قد تتقلب مخاطر التميع أيضا. تستحق رواسب التربة التي صنعها الإنسان الاهتمام أيضا. من المرجح جدا أن تكون الحشوات السائبة، مثل تلك الموضوعة بدون ضغط، عرضة للتميع. يظل استقرار السدود الهيدروليكية وأكوام مخلفات المناجم، حيث تترسب جزيئات التربة بشكل هش عن طريق الترسيب عبر الماء، من المخاطر الزلزالية المعاصرة المهمة. من ناحية أخرى، من غير المرجح أن تلبي الحشوات المضغوطة جيدا معايير الحالة لقابلية التميع.

– معايير التركيب:

نظرا لأن التميع يتطلب تطوير ضغط مسام زائد، فإن قابلية التميع تتأثر بالخصائص التركيبية التي تؤثر على سلوك التغير في الحجم. تميل الخصائص التركيبية المرتبطة بإمكانية تغير الحجم العالية إلى الارتباط بقابلية التميع العالية. تتضمن هذه الخصائص حجم الجسيمات وشكلها وتدرجها. لسنوات عديدة، كان يُعتقد أن الظواهر المرتبطة بالتميع تقتصر على الرمال. اعتُبرت التربة ذات الحبيبات الدقيقة غير قادرة على توليد ضغوط المسام العالية المرتبطة عادة بالتميع، واعتُبرت التربة ذات الحبيبات الخشنة نفاذة للغاية بحيث لا تتحمل أي ضغط مسام متولد لفترة كافية لتطور التميع. في الآونة الأخيرة، اتسعت حدود معايير التدرج لقابلية التميع. وقد لوحظت عملية تميع الطمي غير اللدن (Ishihara, 1984, 1985) في المختبرات والحقول، مما يشير إلى أن خصائص اللدونة وليس حجم الحبيبات وحدها تؤثر على قابلية تميع التربة ذات الحبيبات الدقيقة. الطمي الخشن ذو شكل الجسيمات الضخمة، والذي لا يتمتع باللدونة ولا يتمتع بالتماسك، يكون عرضة تمامًا للتميع (Ishihara, 1993)؛ الطمي الدقيق ذو الجسيمات المتقشرة أو الشبيهة بالصفائح يظهر عموما تماسكا كافيا لمنع التميع. يظل الطين غير قابلة للتميع، على الرغم من أن الطين الحساس يمكن أن يظهر سلوك تليين الإجهاد مشابها لسلوك التربة المتميعة. يمكن اعتبار التربة ذات الحبيبات الدقيقة التي تلبي كلًا من المعايير الصينية الأربعة التالية (Wang, 1979) عرضة لفقدان كبير في القوة:

الأجزاء أدق من 0.005 مم <= 15%

حد التميع <= %35

محتوى الماء الطبيعي >= 0.9

مؤشر التميع <= 0.75

لمراعاة الاختلافات في الممارسات الصينية والأمريكية، قام سلاح المهندسين بالجيش الأمريكي بتعديل خصائص المؤشر المقاسة (عن طريق تقليل محتوى الأجزاء بنسبة 5%، وزيادة حد السيولة بنسبة 1%، وزيادة محتوى الماء الطبيعي بنسبة 2%) قبل تطبيق المعايير الصينية على الطمي الطيني في أساس سد سرديس ((Finn et al., 1994. وفي الطرف الآخر من طيف حجم الحبيبات، لوحظت عملية تمييع الحصى في الحقل (Coulter and Migliaccio, 1966; Chang, 1978; Wong, 1984; Youd et al., 1985, Yegian et al., 1994) وفي (Wong et al., 1975; Evans and Seed, 1987). ويعتقد الآن أن تأثيرات اختراق الغشاء مسؤولة عن مقاومة التميع العالية التي لوحظت في التحقيقات المعملية المبكرة للتربة الحصوية. وعندما يعوق تبديد ضغط المسام وجود طبقات غير منفذة بحيث توجد ظروف غير مستنزفة حقا، يمكن أن تكون التربة الحصوية أيضا عرضة للتميع.

معايير الحالة:

حتى لو كانت التربة تلبي جميع المعايير السابقة لقابلية التميع، فإنها قد تكون أو لا تكون قابلة للتميع. كما تعتمد قابلية التميع على الحالة الأولية للتربة (أي خصائص الإجهاد والكثافة في وقت الزلزال). ونظرًا لأن الميل إلى توليد ضغط مسام زائد لتربة معينة يتأثر بشدة بكل من الكثافة وظروف الإجهاد الأولية، فإن قابلية التميع تعتمد بشدة على الحالة الأولية للتربة. تختلف معايير قابلية التميع هذه، على عكس تلك التي تمت مناقشتها سابقًا، بالنسبة للتميع التدفقي والحركة الدورية. لتقديم أساليب معاصرة لتقييم معايير الحالة (ولتوفير خلفية لتقييم تأثيرات التميع)، يلزم إجراء مراجعة تاريخية موجزة لبعض المفاهيم الأساسية لسلوك التربة غير المتماسكة.

– نسبة الفراغات الحرجة:

في عمله الرائد على قوة القص للتربة، أجرى Casagrande (1936) اختبارات ثلاثية المحاور محكومة بالإجهاد ومستنزفة على عينات رملية هشة وكثيفة في البداية. أظهرت النتائج (الشكل 9.5)، والتي تشكل حجر الزاوية للفهم الحديث لسلوك قوة التربة، أن جميع العينات التي تم اختبارها عند نفس ضغط الاحتواء الفعال اقتربت من نفس الكثافة عند القص إلى إجهادات كبيرة. انكمشت العينات السائبة في البداية، أو تكثفت، أثناء القص وانكمشت العينات الكثيفة في البداية، ولكن بعد ذلك بدأت في التمدد بسرعة كبيرة. عند الإجهادات الكبيرة، اقتربت جميع العينات من نفس الكثافة واستمرت في القص بمقاومة قص ثابتة. تم تسمية نسبة الفراغ المقابلة لهذه الكثافة الثابتة بنسبة الفراغ الحرجة، e_c. من خلال إجراء الاختبارات عند ضغوط حصر فعالة مختلفة، وجد كاساجراند أن نسبة الفراغ الحرجة كانت مرتبطة بشكل فريد بضغط الاحتواء الفعال، وأطلق على الموقع خط نسبة الفراغ الحرجة (CVR) (الشكل 9.6). من خلال تحديد حالة التربة من حيث نسبة الفراغ والضغط الاحتجازي الفعال، يمكن استخدام خط CVR لتحديد الحدود بين الحالات السائبة (الانكماشية) والكثيفة (التمددية). لم تكن المعدات اللازمة لقياس ضغط المسام متاحة في ذلك الوقت، لكن كاساجراند افترض أن الاختبار غير المستنزف الذي يتم التحكم فيه بالإجهاد من شأنه أن ينتج ضغط مسام زائد موجب (بسبب ميل الانكماش) ​​في العينات السائبة، وضغط مسام زائد سالب (بسبب ميل التمدد) في العينات الكثيفة (الشكل 9.7)، حتى تم الوصول إلى خط CVR. تم التحقق من هذه الفرضية لاحقًا تجريبياً. لذلك وصف خط CVR الحالة التي ستنتقل إليها أي عينة تربة عند إجهادات كبيرة، سواء من خلال تغييرات الحجم في ظل ظروف الاستنزاف، أو تغييرات في ضغط الاحتجاز الفعال في ظل ظروف عدم الاستنزاف، أو بعض التركيبات في ظل ظروف الاستنزاف الجزئي.

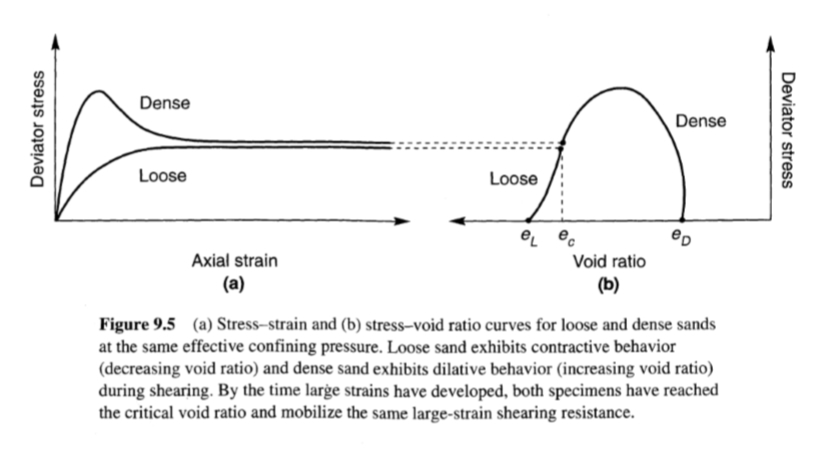
الشكل(9.5)

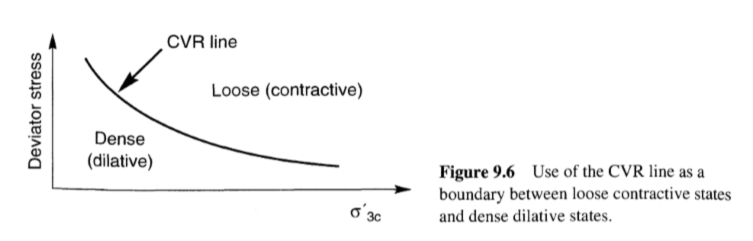
الشكل(9.6)

الشكل(9.7)

نظرًا لأن خط CVR يمثل الحد الفاصل بين السلوك الانكماشي والتمددي، فقد اعتُبر أنه يمثل الحد الفاصل بين الحالات التي تكون فيها تربة معينة عرضة أو غير معرضة للتميع التدفقي (الشكل 9.8). اعتُبرت التربة المشبعة ذات نسب التذبذب الأولية المرتفعة بما يكفي لرسمها فوق خط CVR معرضة للتميع التدفقي، بينما اعتُبرت التربة ذات الحالات الأولية المرسومة أسفل خط CVR غير معرضة للتميع التدفقي. ومع ذلك، عندما عانى سد فورت بيك في مونتانا من فشل تميع التدفق الثابت لمنحدره العلوي أثناء البناء في عام 1938 (Middlebrooks, 1942)، أظهر تحقيق ما بعد الفشل أن الحالة الأولية للتربة التي تعرضت للتميع بشكل واضح كانت في الواقع أقل إلى حد ما من خط CVR (أي في المنطقة غير المعرضة للتميع التدفقي). وقد عزا كاساجراندي هذا التناقض إلى عدم قدرة الاختبارات التي يتم استنزافها تحت التحكم في الإجهاد على تكرار جميع الظواهر التي تؤثر على سلوك التربة في ظل الظروف غير المستنزفة التي يتم التحكم فيها بالإجهاد لفشل التميع التدفقي الفعلي. وعلى مر السنين، طور كاساجراندي الفرضية القائلة بأن الرمل المسال المتدفق له “بنية تدفق” تدور فيها الحبيبات باستمرار لتوجيه نفسها في بنية ذات مقاومة احتكاكية دنيا (Casagrande, 1976). ولم يتمكن كاساجراندي من تحقيق بنية تدفق في المختبر حتى أواخر الستينيات، عندما أجرى أحد طلابه سلسلة مهمة من الاختبارات الثلاثية المحاور غير المستنزفة التي يتم التحكم فيها بالإجهاد (Castro, 1969).

الشكل(9.8)

– حالة التشوه الثابتة

أجرى Castro (1969) اختبارات ثلاثية المحاور ثابتة ودورية على عينات متماسكة بشكل متساوي الخواص وعدة اختبارات ثابتة على عينات متماسكة بشكل غير متساو الخواص. وقد لوحظت ثلاثة أنواع مختلفة من سلوك الإجهاد والانفعال، موضحة للعينات المتماسكة بشكل غير متساو الخواص في (الشكل 9.9). أظهرت العينات الرخوة للغاية (مثل العينة a في الشكل 9.9) قوة ذروة غير مستنزفة عند إجهاد قص صغير ثم “انهارت” لتتدفق بسرعة إلى إجهادات كبيرة عند ضغط احتواء فعال منخفض وقوة إجهاد كبيرة منخفضة. تم وصف هذا النوع من السلوك المعروف الآن باسم التميع التدفقي في ذلك الوقت باسم “التميع”. انكمشت العينات الكثيفة (العينة b) في البداية ثم تمددت حتى تم الوصول إلى ضغط احتواء فعال ثابت مرتفع نسبيًا وقوة إجهاد كبيرة. عند الكثافات المتوسطة (العينة c)، فإن تجاوز قوة الذروة عند إجهاد منخفض تبعه فترة محدودة من سلوك تليين الإجهاد، والذي انتهى ببداية التمدد عند الإجهادات المتوسطة. [يحدث هذا الانعكاس من السلوك الانكماشي إلى السلوك التمددي عند نقطة تحول الطور  (Ishihara et al., 1975)]. أنتج المزيد من التحميل تمددًا مستمرًا إلى ضغوط احتواء فعالة أعلى، وبالتالي قوى إجهاد كبيرة أعلى. أطلق على هذا النوع من السلوك اسم التميع المحدود. أظهر برنامج الاختبار علاقة فريدة بين نسبة الفراغ وضغط الاحتواء الفعال عند الإجهادات الكبيرة. بيانياً، تم رسم هذه العلاقة أدناه وبالتوازي تقريبًا مع خط CVR الذي تم الحصول عليه من اختبارات التحكم في الإجهاد المفرغة؛ ويعزى الاختلاف إلى تطور بنية التدفق في ظل ظروف التحكم في الإجهاد. تم تعريف الحالة التي تتدفق فيها التربة باستمرار تحت إجهاد قص ثابت وضغط احتواء فعال ثابت عند حجم ثابت وسرعة ثابتة لاحقًا  (Castro and Poulos, 1977; Poulos, 1981) على أنها الحالة المستقرة للتشوه. نظرًا لأن الحالة المستقرة للتشوه لا يتم الوصول إليها إلا عند إجهادات كبيرة (بعد إخفاء تأثيرات الظروف الأولية مثل نسيج التربة وتاريخ الإجهاد والانفعال وظروف التحميل)، فقد اعتُبر أن الضغط الاحترازي الفعال في عنصر من التربة في الحالة المستقرة للتشوه يعتمد فقط على كثافة التربة. وقد ثبت مؤخرًا نسبيًا أن ظروف الحالة المستقرة تختلف بالنسبة لمسارات الإجهاد الانضغاطي والتمددي (Vaid et al., 1990; Reimer and Seed, 1992; Vaid and Thomas, 1995)، وخاصةً عندما تترسب التربة ببنية متباينة الخواص بطبيعتها. على وجه التحديد، تظهر الرمال المبللة سلوكًا انكماشيًا على مدى أوسع من الكثافات عند تحميلها بالامتداد مقارنة بالضغط؛ قد يظهر عنصر معين من الرمل بكثافة متوسطة سلوكًا تمدديًا في الضغط ولكن سلوكًا انكماشيًا عند تحميله بالامتداد. ونتيجة لذلك، يجب أن تتطابق الظروف الترسيبية وظروف الإجهاد وظروف التحميل الموجودة في الحقل عن كثب قدر الإمكان في التحقيقات المعملية لسلوك الحالة المستقرة. يُطلق على موضع النقاط التي تصف العلاقة بين نسبة الفراغ والضغط الاحتجازي الفعال في الحالة المستقرة للتشوه اسم خط الحالة المستقرة (SSL). في شكله الأكثر عمومية، يمكن اعتبار SSL منحنى ثلاثي الأبعاد في e-σ’-τ (الشكل 9.10) أو فضاء e-p’-q. وبالتالي، يمثل SSL الموضح في الشكل (9.7a) إسقاط SSL ثلاثي الأبعاد على مستوى ثابت τ. يمكن أيضًا إسقاط SSL على مستويات ذات ضغط احتجاز فعال ثابت (σ’ = ثابت) وكثافة ثابتة (e = ثابت). يمكن أيضًا التعبير عن SSL من حيث قوة الحالة المستقرة، S_su؛ نظرًا لأن مقاومة القص للتربة في الحالة المستقرة للتشوه تتناسب مع ضغط الاحتواء الفعال، فإن SSL المستندة إلى القوة تكون موازية لـ SSL المستندة إلى ضغط الاحتواء الفعال عندما يتم رسم كليهما على مقاييس لوغاريتمية (الشكل 9.11).

الشكل(9.9)

الشكل(9.10)

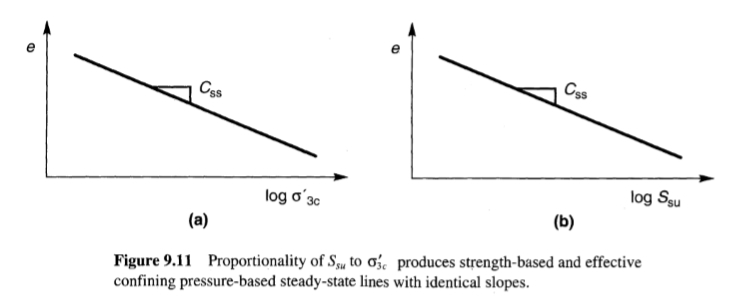
الشكل(9.11)

إن خط الحالة الساكنة مفيد لتحديد الظروف التي قد تكون أو لا تكون فيها تربة معينة عرضة للتميع التدفقي (الشكل 9.12). التربة التي تظهر حالتها أسفل خط الحالة الساكنة ليست عرضة للتميع التدفقي. التربة التي تظهر حالتها أعلى من خط الحالة الساكنة ستكون عرضة للتميع التدفقي فقط إذا تجاوز إجهاد القص الساكن قوتها في الحالة المستقرة (أو المتبقية). نظرًا لأنه يمكن استخدام خط الحالة الساكنة لتقييم مقاومة القص للتربة المتميعة، فهو مفيد أيضًا لتقييم التأثيرات المحتملة للتميع. على الرغم من أن تحديد موضع خط الحالة الساكنة قد يكون صعبًا في الممارسة العملية، فإن خط الحالة الساكنة مفيد جدًا لفهم المفاهيم الأساسية للتميع. من ناحية أخرى، يمكن أن تحدث الحركة الدورية في التربة التي تظهر حالتها أعلى أو أسفل خط الحالة الساكنة. بعبارة أخرى، يمكن أن تحدث الحركة الدورية في كل من التربة الرخوة والكثيفة.

إن موقع خط الحالة المستقرة حساس للخصائص التركيبية للتربة – حيث يتأثر موضعها الرأسي بشدة بالتدرج وانحدارها بزاوية الجسيمات. وعادةً ما يكون للتربة ذات الجسيمات المستديرة خط حالة مستقر مسطح – وهي سمة تؤدي غالبًا إلى صعوبة في تقدير قوة الحالة المستقرة في الموقع.

الشكل(9.12)

معلمة الحالة: توضح طبيعة خط الحالة المستقرة مدى محدودية تطبيق المقاييس المطلقة للكثافة، مثل نسبة الفراغ والكثافة النسبية، لتوصيف التربة القابلة للتميع. وكما هو موضح في (الشكل 9.12)، يمكن أن يكون عنصر من التربة بنسبة فراغ معينة (ومن ثم كثافة معينة وكثافة نسبية) عرضة للتميع التدفقي تحت ضغط احتواء فعال مرتفع ولكنه غير قابل للتعرض عند ضغط احتواء فعال منخفض. باستخدام مفاهيم ميكانيكا التربة في الحالة الحرجة، يجب أن يكون سلوك التربة غير المتماسكة أكثر ارتباطًا بقرب حالتها الأولية من خط الحالة المستقرة منه بالمقاييس المطلقة للكثافة (Roscoe and Pooroshasb, 1963). بعبارة أخرى، يجب أن تظهر التربة في الحالات الواقعة على نفس المسافة من خط الحالة المستقرة سلوكًا مشابهًا. باستخدام هذا المنطق، يمكن تعريف معلمة الحالة (Been and Jeffries, 1985) على أنها:

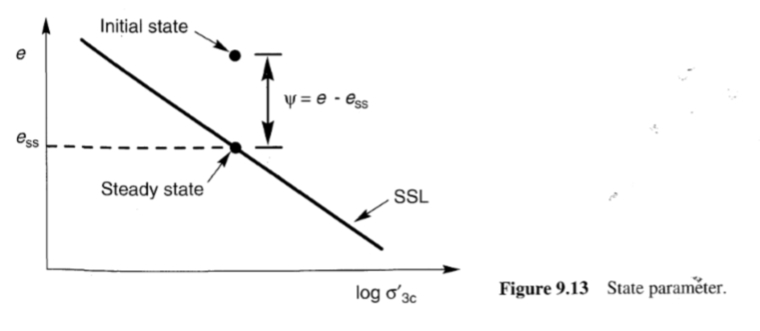
Ψ=e-e_ss

حيث e_ss هي نسبة الفراغ لخط الحالة المستقرة عند ضغط الاحتجاز الفعال محل الاهتمام (الشكل 9.13). عندما تكون معلمة الحالة موجبة، تظهر التربة سلوكًا انكماشيًا وقد تكون عرضة للتميع التدفقي. عندما تكون سالبة، سيحدث سلوك تمددي ولا تكون التربة عرضة للتميع التدفقي. تم ربط معامل الحالة بزاوية الاحتكاك وزاوية التمدد ومقاومة CPT (Been et al., 1986, 1987; Sladen, 1985)، ونتائجPMT  (Yu, 1994)، ونتائج DMT  (Konrad, 1988)،.أظهر  (Ishihara, 1993)  أن قدرة معامل الحالة على توصيف سلوك التربة للرمال السائبة جدًا تحت ضغوط احتواء فعالة منخفضة قد تكون محدودة واقترح معاملًا مماثلًا (مؤشر الحالة) بناءً على المسافة النسبية بين الحالة الأولية وخط الحالة المستقرة تقريبًا (خط مشابه لخط SSL ويقع أسفله قليلاً والذي يتوافق مع ظروف الإجهاد والكثافة عند نقاط تحول الطور الملحوظة في حالات التميع المحدود). يعد مفهوم معامل الحالة مفيدًا للغاية وإمكانية تحديد قيمته من الاختبارات في الموقع جذابة. ومع ذلك، فإن الدقة التي يمكن بها تحديد معلمة الحالة تتأثر بالدقة التي يمكن بها تحديد موضع SSL.

الشكل(9.13)

بدء التميع:

إن حقيقة أن رواسب التربة عرضة للتميع لا تعني بالضرورة أن التميع سوف يحدث في زلزال معين. فحدوثه يتطلب اضطرابًا قويًا بما يكفي لبدء حدوثه أو إثارته. إن تقييم طبيعة هذا الاضطراب هو أحد الأجزاء الأكثر أهمية في تقييم مخاطر التميع. وأي مناقشة لبدء التميع يجب أن تحدد الظواهر المرتبطة بالتميع التي يتم النظر فيها. لقد جمعت العديد من الدراسات السابقة لبدء التميع ضمناً بين التميع التدفقي والحركة الدورية معًا، ولكن نظرًا لأنهما ظاهرتان مختلفتان تمامًا، فمن المناسب النظر في كل منهما على حدة. وعلى الرغم من أن الحركة الدورية ظاهرة مرتبطة بالزلزال، إلا أنه يمكن بدء التميع التدفقي بطرق متنوعة. وقد لوحظت انزلاقات التدفق الناجمة عن التحميل الرتيب (التحلل الساكن) في رواسب التربة الطبيعية (Koppejan et al., 1948; Andersen and Bjerum, 1968; Bjerum, 1971; Kramer, 1988)، والحشوات من صنع الإنسان (Middlebrooks, 1942; Cornforth et al., 1975; Mitchell, 1984)، وأكوام مخلفات المناجم (Kleiner, 1976; Jennings, 1979; Eckersley, 1985). وقد تم تحفيز التميع التدفقي أيضًا من خلال مصادر اهتزازية غير زلزالية، مثل دق الأكوام (Jakobsen, 1952; Broms and Bennennark, 1967)، وحركة القطارات (Fellenius, 1953)، والاستكشاف الجيوفيزيائي (Hryciw et al., 1990) والتفجير (Conlon, 1966; Carter and Seed, 1988). وربما من عجيب المفارقات أن دراسة التميع الثابت على مدى السنوات العشر إلى الخمس عشرة الماضية ساهمت بشكل كبير في تحسين فهم التميع الناجم عن الزلازل من خلال تحديد ظروف الإجهاد الفعالة التي تبدأ عندها ظاهرة التميع. يتطلب فهم بدء التميع تحديد حالة التربة عند تحفيز التميع. في الأقسام التالية، سيتم تقديم هذه الظروف في إطار يسمح بفهم آليات كل من التميع التدفقي والحركة الدورية بشكل واضح. بعد ذلك، سيتم تقديم إجراءات عملية ومستخدمة بشكل شائع لتحديد طبيعة الاضطراب المطلوب للانتقال من الحالة الأولية إلى الحالة التي يتم عندها تحفيز التميع.

– سطح التميع التدفقي:

يمكن توضيح الظروف التي يبدأ عندها التميع التدفقي بسهولة بمساعدة مسار الإجهاد. أظهر Hanzawa et al. (1979) لأول مرة أن ظروف الإجهاد الفعالة التي يحدث عندها سلوك تليين الانفعال في الرمال المشبعة السائبة يمكن وصفها ببساطة شديدة في مساحة مسار الإجهاد. يمكن وصف ظروف الإجهاد الفعالة عند بدء التميع التدفقي في مساحة مسار الإجهاد بواسطة سطح ثلاثي الأبعاد سيتم الإشارة إليه فيما بعد باسم سطح التميع التدفقي (FLS). في حين تظل بعض الصعوبات العملية قائمة في قياس FLS لمسارات الإجهاد العامة، إلا أنها توفر (بالتزامن مع مفاهيم الحالة المستقرة) إطارًا مفيدًا للغاية للفهم المفاهيمي للعلاقات بين ظواهر التميع المختلفة. هذا الفهم المفاهيمي حيوي للتقييم السليم لسلوك التربة القابلة للتميع أثناء وبعد الزلزال.

– التحميل الرتيب

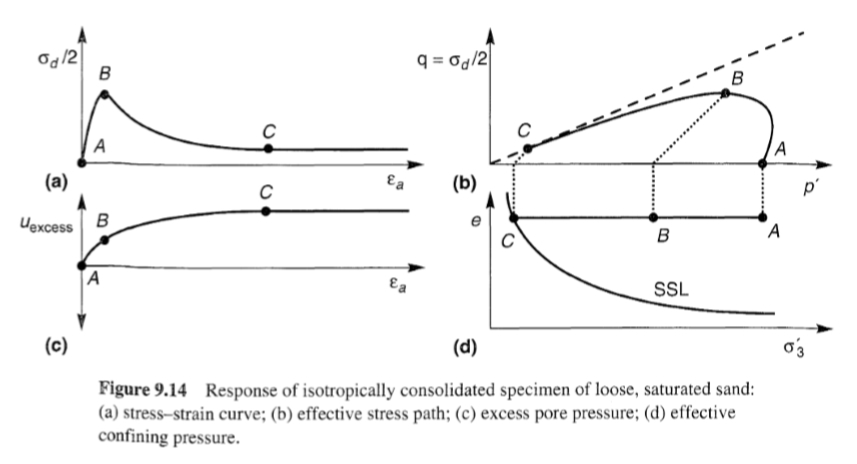
يمكن رؤية الظروف عند بدء تميع التدفق بسهولة أكبر عندما تتعرض التربة لضغوط متزايدة بشكل رتيب. على سبيل المثال، ضع في اعتبارك استجابة عينة متماسكة متساوي الخواص من الرمل المشبع الرخو للغاية في ضغط ثلاثي المحاور غير مستنزف ومتحكم فيه بالإجهاد (الشكل 9.14). مباشرة قبل القص غير المستنزف (النقطة A)، تكون العينة في حالة توازن مستنزف تحت ضغط احتواء فعال أولي σ’_3c؛، مع إجهاد قص صفري (الشكل 9.14 a،b) وضغط مسام زائد صفري (الشكل 9.14 c). نظرًا لأن حالتها الأولية أعلى بكثير من مستوى سطح البحر (الشكل 9.14 d)، فإن الرمل سيظهر سلوكًا انكماشيًا. عندما يبدأ القص غير المستنزف، تولد العينة الانكماشية ضغط مسام زائد موجب حيث تحشد مقاومة القص حتى قيمة الذروة (النقطة B) التي تحدث عند إجهاد صغير نسبيًا. إن ضغط المسام الزائد عند النقطة B صغير نسبيًا أيضًا؛ حيث تكون نسبة ضغط المسام r_u=u_excess/σ’_3c أقل بكثير من 1.00. ومع ذلك، تصبح العينة غير مستقرة عند النقطة B، ولأنها محملة في ظل ظروف يتم التحكم فيها بالإجهاد، فإنها تنهار (قد يزيد الإجهاد المحوري من أقل من 1% إلى أكثر من 20% في جزء من الثانية). ومع إجهاد العينة من النقطة B إلى النقطة C، يزداد ضغط المسام الزائد بشكل كبير. وعند النقطة C وما بعدها، تكون العينة في حالة ثابتة من التشوه ويكون ضغط الاحتواء الفعال جزءًا صغيرًا فقط من ضغط الاحتواء الفعال الأولي. وقد أظهرت هذه العينة سلوك تميع التدفق؛ حيث كانت إجهادات القص الثابتة المطلوبة للتوازن (عند النقطة B) أكبر من قوة القص المتاحة (عند النقطة C) للتربة المتميعة. وقد بدأ تميع التدفق في اللحظة التي أصبحت فيها غير مستقرة بشكل لا رجعة فيه (أي عند النقطة B).

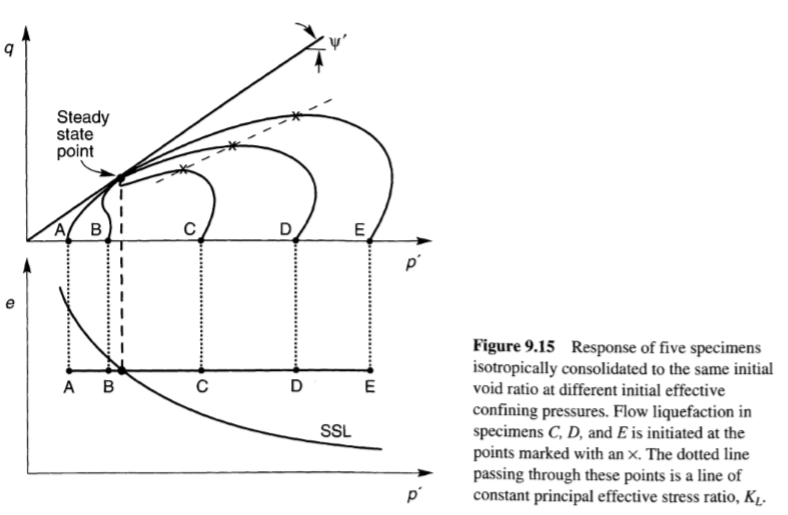
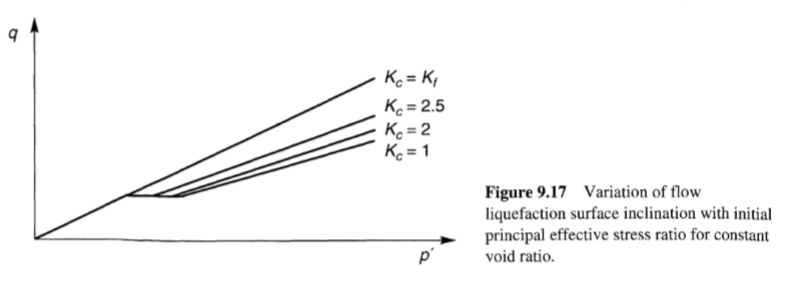
الآن، لننظر في استجابة سلسلة من العينات ثلاثية المحاور التي تم تجميعها في البداية بنفس نسبة الفراغ عند ضغوط احتواء فعالة مختلفة. نظرًا لأن جميع العينات لها نفس نسبة الفراغ، فستصل جميعها إلى نفس ظروف الإجهاد الفعالة في الحالة المستقرة، لكنها ستصل إلى هناك من خلال مسارات إجهاد مختلفة. يوضح (الشكل 9.15) استجابة كل عينة تحت التحميل الرتيب. الحالات الأولية للعينات A وB أقل من SSL، لذا فهي تظهر سلوكًا تمدديًا عند القص. تُظهر العينات C وD وE سلوكًا انكماشيًا؛ كل منها يصل إلى ذروة قوة غير مستنزفة وبعد ذلك تجهد بسرعة نحو الحالة المستقرة. بالنسبة للعينات C وD وE، يبدأ تميع التدفق عند ذروة كل مسار إجهاد (عند النقاط المحددة بعلامة x) Hanzawa et al. (1979), Vaid and Chern (1983)، وعدد من التحقيقات الأحدث أظهرت أن موضع النقاط التي تصف ظروف الإجهاد الفعّالة عند بدء تميع التدفق هو خط مستقيم (الخط المنقط في الشكل 9.15) يمتد عبر أصل مسار الإجهاد. من الناحية البيانية، يمكن استخدام هذه النقاط لتحديد سطح تميع التدفق (FLS) في مساحة مسار الإجهاد؛ نظرًا لأن تميع التدفق لا يمكن أن يحدث إذا كان مسار الإجهاد أقل من نقطة الحالة المستقرة، فإن FLS مقطوع عند هذا المستوى (الشكل 9.16). تم اقتراح هذا الشكل من FLS لأول مرة (باسم مختلف) بواسطة Vaid and Chern (1985). تجدر الإشارة إلى أن (Sladen et al. 1985) اقترحوا سطحًا مشابهًا (يُسمى سطح الانهيار) افترض أنه يمتد خطيًا عبر نقطة الحالة المستقرة؛ نظرًا لأن غلبة الأدلة التجريبية الحالية يبدو أنها تدعم الإسقاط عبر الأصل. بالنسبة للعينات شديدة التفكك، قد تكون نقطة الحالة المستقرة قريبة جدًا من الأصل بحيث يكون الاختلاف العملي بين FLS وسطح الانهيار ضئيلًا. تحدد FLS الحد الفاصل بين الحالات المستقرة وغير المستقرة في القص غير المستنزف. إذا وصلت ظروف الإجهاد في عنصر من عناصر التربة إلى FLS في ظل ظروف غير مستنزفة، سواء عن طريق التحميل الرتيب أو الدوري، فسيتم تشغيل تميع التدفق وستقل مقاومة القص إلى قوة الحالة المستقرة. لذلك، تصف FLS الظروف التي يبدأ فيها تميع التدفق. بالنسبة للظروف الأولية المتساوية الخواص، غالبًا ما يكون منحدر FLS حوالي ثلثي المنحدر للرمال النظيفة. ومع ذلك، تشير العينات التي تم اختبارها في ظل ظروف أولية متباينة الخواص إلى أن FLS أكثر انحدارًا للتربة ذات إجهاد القص الأولي (المستنزف) العالي مقارنة بالتربة ذات إجهاد القص الأولي المنخفض بنفس نسبة الفراغ (الشكل 9.17). قد يكون FLS قريبًا جدًا من نقطة الإجهاد الأولية عندما تكون إجهادات القص الأولية كبيرة، وفي هذه الحالة قد يبدأ تميع التدفق من خلال اضطراب صغير جدًا غير مستنزف (Kramer and Seed, 1988). ربما تضمنت الحالات التاريخية التي نُسبت إلى التميع التلقائي إجهادات قص أولية كانت عالية بما يكفي بحيث لم يتم ملاحظة الاضطراب الصغير غير المستنزف المطلوب لبدء تميع التدفق. إن سلوك التميع المحدود الذي أظهرته العينات C وD (الشكل 9.16) مهم للحالات التي يزداد فيها إجهاد القص الثابت (كما في حالة التحميل الرتيب الموضحة هنا). في مثل هذه الحالات، قد تنخفض مقاومة القص إلى قيم عند نقطة تحول الطور (أو الحالة شبه المستقرة) أقل من قوة الحالة المستقرة. وقد يؤدي هذا الانخفاض المؤقت في مقاومة القص إلى إحداث إجهادات قص تتراوح بين 5% إلى 20% (Ishihara, 1993) وينتج عنه تشوهات دائمة كبيرة وغير مقبولة. ولأن تأثيرات الظروف الأولية لا تُمحى تمامًا عند مستويات الإجهاد هذه، فإنها تؤثر على قوة الحالة شبه المستقرة. وقد قدم إيشيهارا إجراءات لتقدير قوة الحالة شبه المستقرة. ولأن المكون الثابت لإجهاد القص يظل ثابتًا بشكل عام أو يتناقص أثناء الزلازل، فإن احتمالية الوصول إلى الحالة شبه المستقرة أقل نتيجة للزلزال.

الشكل(9.14)

الشكل(9.15)

الشكل(9.16)

الشكل(9.17)

– التحميل الدوري:

أظهر Vaid and Chern (1983) لأول مرة أن نموذج FLS ينطبق على كل من التحميل الدوري والرتيب، وهناك قدر كبير من الأدلة التجريبية المستقلة تدعم هذه الملاحظة. تشير الأدلة التجريبية الأخرى (على سبيل المثال، Alarcon-Guzman et al., 1988) إلى أن مسار الإجهاد الفعال يمكن أن يتحرك إلى حد ما خارج نموذج FLS قبل أن يبدأ التميع بواسطة التحميل الدوري. لا يُعرف حاليًا على وجه اليقين ما إذا كان التميع يبدأ بدقة عند نموذج FLS تحت التحميل الدوري والرتيب. نظرًا لاستخدام نموذج FLS كجزء من نموذج مفاهيمي لسلوك التميع، فسيتم افتراض أن نموذج FLS ينطبق على كل من التحميل الدوري والرتيب.

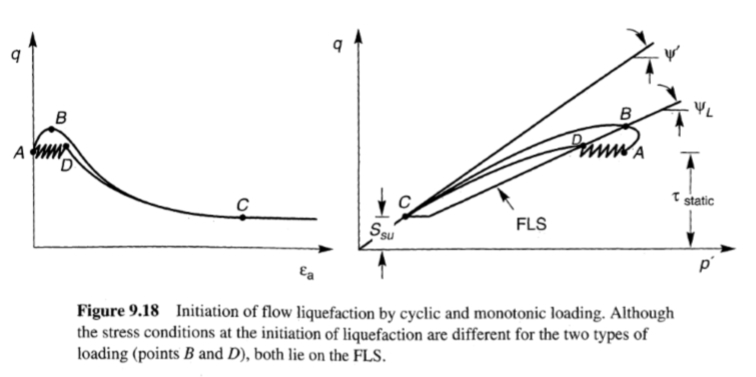
ضع في اعتبارك استجابات عينتين متطابقتين ومتماسكتين بشكل غير متجانس وثلاثي المحاور من الرمل المشبع السائب (الشكل 9.18). في البداية، تكون العينات في حالة توازن مفرغ (النقطة A) تحت إجهاد قص ثابت τ_static أكبر من قوة الحالة المستقرة، S_su. يتم تحميل العينة الأولى بشكل رتيب تتراكم مقاومة القص إلى قيمة الذروة عندما يصل مسار الإجهاد FLS إلى (النقطة B). عند هذه النقطة تصبح العينة غير مستقرة وتتعرض لإجهاد سريع نحو الحالة المستقرة (النقطة C). يتم تحميل العينة الثانية بشكل دوري يتحرك مسار الإجهاد الفعال إلى اليسار مع تطور ضغوط المسام الزائدة الإيجابية وتراكم الإجهادات الدائمة. عندما يصل مسار الإجهاد الفعال إلى FLS (عند النقطة D)، تصبح العينة غير مستقرة وتتعرض لإجهاد نحو الحالة المستقرة للتشوه (النقطة C). على الرغم من أن ظروف الإجهاد الفعال عند بدء التميع (النقطتين B وD) كانت مختلفة، إلا أنها وقعت في كلتا الحالتين على FLS. وبالتالي، فإن FLS يمثل بداية عدم الاستقرار الذي ينتج عنه التميع التدفقي. قدم Lade (1992) وصفًا تفصيليًا لعدم الاستقرار هذا.

– تطور التميع التدفقي يحدث التميع التدفقي في مرحلتين. المرحلة الأولى، التي تحدث عند مستويات إجهاد صغيرة، تتضمن توليد ضغط مسام زائد كافٍ لتحريك مسار الإجهاد من موضعه الأولي إلى FLS. يمكن توليد ضغط المسام الزائد هذا من خلال التحميل الرتيب أو الدوري. عندما يصل مسار الإجهاد الفعال إلى FLS، تصبح التربة غير مستقرة بطبيعتها وتبدأ المرحلة الثانية. تتضمن المرحلة الثانية تليين الإجهاد (وتوليد ضغط مسام زائد إضافي) مدفوعًا بإجهادات القص المطلوبة للتوازن الثابت. هذه الإجهادات القصية هي الإجهادات المحركة – يجب تمييزها عن الإجهادات التي تتطور أثناء ترسب وتصلب التربة (Castro، 1991). تتطور إجهادات كبيرة في المرحلة الثانية مع انتقال مسار الإجهاد الفعال من FLS إلى الحالة المستقرة. إذا أخذت المرحلة الأولى التربة إلى FLS في ظل ظروف غير مستنزفة وخاضعة للإجهاد، فإن المرحلة الثانية أمر لا مفر منه.

– تأثير الضغط الزائد للمسام:

إن توليد الضغط الزائد للمسام هو المفتاح لبدء التميع. فبدون تغييرات في ضغط المسام، وبالتالي تغييرات في الإجهاد الفعال، لا يمكن حدوث التميع التدفقي أو الحركة الدورية. ومع ذلك، يمكن للظواهر المختلفة أن تتطلب مستويات مختلفة من ضغط المسام لكي تحدث.

– التميع التدفقي:

يمكن بدء التميع التدفقي عن طريق التحميل الدوري فقط عندما يكون الإجهاد القصي المطلوب للتوازن الساكن أكبر من قوة الحالة المستقرة. في الحقل، تحدث إجهادات القص هذه بسبب الجاذبية وتظل ثابتة بشكل أساسي حتى تتطور تشوهات كبيرة. لذلك، فإن الحالات الأولية التي يتم رسمها في المنطقة المظللة في (الشكل 9.19) معرضة للتميع التدفقي. ومع ذلك، فإن حدوث التميع التدفقي يتطلب اضطرابًا غير مستنزف قويًا بما يكفي لتحريك مسار الإجهاد الفعال من نقطته الأولية إلى FLS.

إذا تم رسم ظروف الإجهاد الأولية بالقرب من FLS، كما هو الحال في عنصر التربة المعرض لإجهادات قص كبيرة، يمكن أن يحدث تميع التدفق عن طريق ضغوط مسام زائدة صغيرة (Karter and Seed, 1988). ستكون مقاومة التميع أكبر إذا كانت ظروف الإجهاد الأولية أبعد عن سطح تميع التدفق. يمكن استخدام FLS لتقدير نسبة ضغط المسام عند بدء تميع التدفق؛ فهي تنخفض بشكل كبير مع زيادة نسبة الإجهاد الأولية (الشكل 9.20) للتربة عند نسبة فراغ معينة. عند نسب إجهاد أولية عالية، يمكن أن يحدث تميع التدفق عن طريق اضطرابات ثابتة أو ديناميكية صغيرة جدًا.

– الحركة الدورية:

على الرغم من عدم إمكانية حدوث تميع التدفق، إلا أن الحركة الدورية يمكن أن تتطور عندما يكون إجهاد القص الثابت أصغر من قوة القص في الحالة المستقرة. لذلك، فإن الحالات الأولية التي يتم رسمها في المنطقة المظللة من (الشكل 9.21) عرضة للحركة الدورية. لاحظ أن الحركة الدورية يمكن أن تحدث في كل من التربة الرخوة والكثيفة (تمتد المنطقة المظللة في الشكل 9.21 من ضغوط الاحتواء الفعالة المنخفضة جدًا إلى العالية جدًا وتتوافق مع الحالات التي يمكن رسمها فوق وأسفل مستوى سطح البحر). يمكن توضيح تطور الحركة الدورية من خلال استجابة التربة في الاختبارات ثلاثية المحاور الدورية. تنتج ثلاث مجموعات من الظروف الأولية وظروف التحميل الدوري عمومًا حركة دورية.

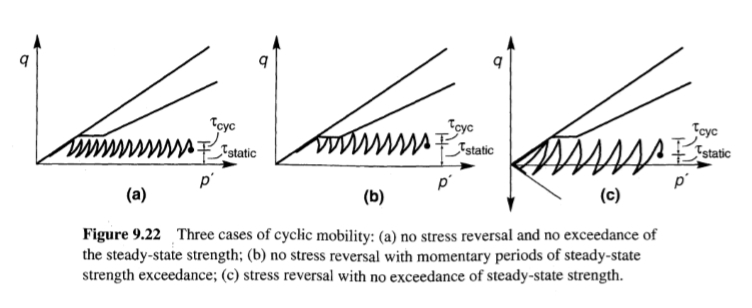
يحدث الأول، كما هو موضح في الشكل 9.22 a، عندما تكون τ_static-τ_cyc> 0 (أي لا يوجد انعكاس لإجهاد القص) وτ_static+τ_cyc < S_su (لا يوجد تجاوز لقوة الحالة المستقرة). في هذه الحالة، يتحرك مسار الإجهاد الفعال إلى اليسار حتى يصل إلى غلاف الفشل المستنزف. نظرًا لأنه لا يمكنه عبور غلاف الفشل المستنزف، فإن دورات التحميل الإضافية تتسبب ببساطة في تحركه لأعلى ولأسفل على طول الغلاف. ونتيجة لذلك، تستقر ظروف الإجهاد الفعال. لا يمكن أن تتطور التشوهات من نوع التدفق لأن أي إجهاد أحادي الاتجاه من شأنه أن يحفز التمدد. انخفض ضغط الاحتواء الفعال بشكل كبير، ويمكن أن تسمح الصلابة المنخفضة الناتجة بتطور إجهادات دائمة كبيرة في كل دورة تحميل. يحدث الشرط الثاني (الشكل 9.22b ) عندما تكون τ_static-τ_cyc> 0 (لا يوجد انعكاس للإجهاد) و τ_static+τ_cyc > S_su(يتم تجاوز قوة الحالة المستقرة مؤقتًا). مرة أخرى، سيتسبب التحميل الدوري في تحرك مسار الإجهاد الفعال إلى اليسار. عندما يلامس FLS، ستحدث فترات مؤقتة من عدم الاستقرار. قد يتطور إجهاد دائم كبير خلال هذه الفترات، خاصةً إذا كانت τ_static أكبر من قوة القص شبه الساكنة، لكن الإجهاد سيتوقف عمومًا في نهاية التحميل الدوري عندما يعود إجهاد القص إلى τ_static. الشرط الأخير هو أن يكون τ_static-τ_cyc< 0 (يحدث انعكاس للإجهاد) و τ_static+τ_cyc < S_su(لا يتم تجاوز قوة الحالة المستقرة). في هذه الحالة (الشكل 9.22c ) يتغير اتجاه إجهاد القص بحيث تتضمن كل دورة كل من التحميل الانضغاطي والتمديدي. وقد أظهرت الأدلة التجريبية (Dobry et al., 1982; Mohamad and Dobry, 1986) أن معدل توليد ضغط المسام يزداد مع زيادة درجة عكس الإجهاد. وبالتالي فإن مسار الإجهاد الفعال يتحرك بسرعة نسبية إلى اليسار (لأن ضغط المسام الزائد يتراكم بسرعة) ويتذبذب في النهاية على طول أجزاء الضغط والتمديد لحدود الفشل المستنزف. وفي كل مرة يمر فيها مسار الإجهاد الفعال عبر الأصل (يفعل ذلك مرتين خلال كل دورة تحميل)، تكون العينة في حالة لحظية من الإجهاد الفعال الصفري (r_u=100%). وعلى الرغم من أن هذه الحالة من الإجهاد الفعال الصفري يشار إليها باسم التميع الأولي ((Seed and Lee, 1966، فلا ينبغي أن يُفهم من ذلك أن التربة ليس لديها قوة قص. إذا تم تطبيق تحميل رتيب في حالة التميع الأولي، فإن العينة سوف تتمدد حتى يتم تعبئة قوة الحالة المستقرة (الشكل 9.23). قد تتراكم إجهادات دائمة كبيرة أثناء التحميل الدوري، ولكن لا يمكن أن يحدث فشل التدفق. لاحظ أن التميع الأولي لا يمكن أن يحدث إلا عندما تحدث انعكاسات الإجهاد. وعلى النقيض من التميع التدفقي، لا توجد نقطة واضحة تبدأ عندها الحركة الدورية. تتراكم الإجهادات الدائمة والتشوهات الدائمة التي تنتجها بشكل تدريجي. يعتمد حجمها على إجهاد القص الساكن ومدة حركة الأرض. بالنسبة لحركات الأرض قصيرة المدة في المواقع المستوية تقريبًا، قد تكون التشوهات الدائمة صغيرة. بالنسبة للمواقع ذات المنحدر المعتدل أو المواقع ذات المنحدر اللطيف المعرضة لحركات أرضية طويلة المدة، يمكن أن تنتج الحركة الدورية مستويات ضارة من تشوه التربة.

الشكل(9.18)

الشكل(9.19)

الشكل(9.20)

الشكل(9.21)

الشكل(9.22)

الشكل(9.23)

– تقييم بدء التميع:

إن الجمع بين مفهومي سطح التميع في الحالة الثابتة والتدفق يوفر إطارًا يمكن من خلاله فهم الآليات الأساسية للتميع. ويدمج هذا الإطار قابلية التميع مع بدء التميع وتأثيراته. كما يوضح التأثير المهم لتوليد ضغط المسام الزائد على مدى المخاطر المرتبطة بالتميع. وقد تطور عدد من الأساليب لتقييم إمكانية بدء التميع على مر السنين. في التالي، يتم تقديم أكثر هذه الأساليب شيوعًا. ولكل منهما مزايا وقيود، ويفضل كل منهما مجموعات مختلفة من المهندسين. وبالنسبة للمشاريع المهمة بشكل خاص، فليس من غير المعتاد استخدام أكثر من نهج واحد في تقييم مخاطر التميع.

– نهج الإجهاد الدوري

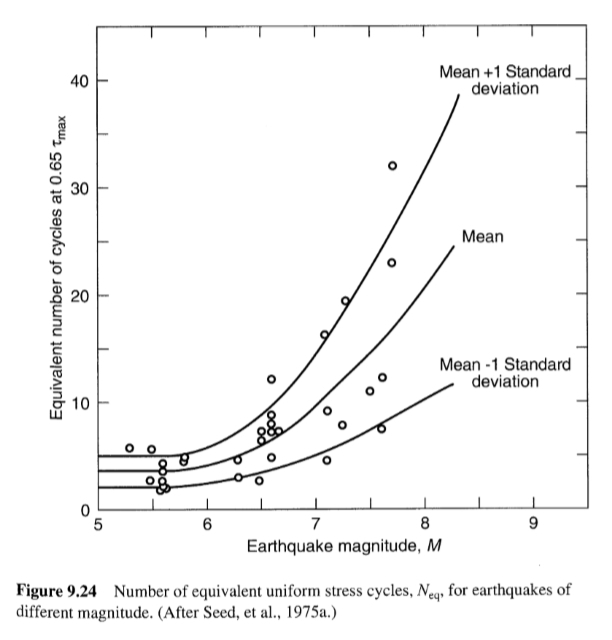
في الستينيات والسبعينيات من القرن العشرين، نتج العديد من التطورات في حالة معرفة ظاهرة التميع عن العمل الرائد الذي قام به سيد وزملاؤه في جامعة كاليفورنيا في بيركلي. وقد اتجه هذا البحث إلى حد كبير نحو تقييم ظروف التحميل المطلوبة لتحفيز التميع. وقد تم وصف هذا التحميل من حيث إجهادات القص الدورية، وتم تقييم إمكانية التميع على أساس سعة وعدد دورات إجهاد القص الناتج عن الزلزال. وقد أصبح النهج العام معروفًا باسم نهج الإجهاد الدوري. وقد عرّف Seed and Lee (1966) التميع الأولي على أنه النقطة التي يصبح فيها زيادة ضغط المسام مساوية لضغط الاحتجاز الفعال الأولي [أي عندما تكون u_excess=σ’_3c  (أو عندما تكون r_u=100%)]. نظرًا لأن معظم التحقيقات المبكرة في الاختبارات المعملية كانت تستند إلى اختبارات ثلاثية المحاور دورية على عينات متماسكة متساوي الخواص (وبالتالي، مع عكس الإجهاد الكامل)، يمكن إنتاج التميع الأولي في كل من العينات السائبة والكثيفة. وفقًا لما سبق، سيتم تصنيف هذا السلوك الآن (نظرًا لأن إجهاد القص الثابت كان صفرًا) على أنه حركة دورية. أدى استخدام مصطلح التميع الأولي بالعديد من الأشخاص إلى الاعتقاد الخاطئ بأن التميع التدفقي يمكن أن يبدأ في أي تربة فضفاضة أو كثيفة غير متماسكة. إن نهج الإجهاد الدوري بسيط للغاية من الناحية المفاهيمية: تتم مقارنة التحميل الناجم عن الزلزال، المعبر عنه من حيث إجهادات القص الدورية، بمقاومة التميع للتربة، المعبر عنها أيضًا من حيث إجهادات القص الدورية. في المواقع التي يتجاوز فيها التحميل المقاومة، من المتوقع حدوث التميع. إن تطبيق نهج الإجهاد الدوري يتطلب الاهتمام الدقيق بالطريقة التي يتم بها تحديد ظروف التحميل ومقاومة التميع. تحديد حمولة الزلازل. إن مستوى ضغط المسام الزائد المطلوب لبدء التميع مرتبط بسعة ومدة التحميل الدوري الناتج عن الزلزال. ويستند نهج الإجهاد الدوري إلى افتراض أن توليد ضغط المسام الزائد مرتبط بشكل أساسي بإجهادات القص الدورية، وبالتالي فإن التحميل الزلزالي يتم التعبير عنه من حيث إجهادات القص الدورية. ويمكن التنبؤ بالحمل بطريقتين: من خلال تحليل مفصل لاستجابة الأرض أو باستخدام نهج مبسط. ويمكن استخدام تحليلات استجابة الأرض للتنبؤ بالتاريخ الزمني لإجهاد القص على أعماق مختلفة داخل رواسب التربة. وتنتج مثل هذه التحليلات تواريخ زمنية ذات خصائص عابرة وغير منتظمة لحركات الزلازل الفعلية. ومع ذلك، فإن البيانات المعملية التي يمكن من خلالها تقدير مقاومة التميع يتم الحصول عليها عادةً من الاختبارات التي يكون فيها لإجهادات القص الدورية سعات موحدة. لذلك، تتطلب مقارنة التحميل الناجم عن الزلزال بالمقاومة المحددة في المختبر تحويل تاريخ زمني غير منتظم لإجهاد القص إلى سلسلة مكافئة من دورات الإجهاد المنتظمة. طبق Seed et al (1975) إجراء ترجيح لمجموعة من سجلات زمنية لإجهاد القص من حركات أرضية قوية مسجلة لتحديد عدد دورات الإجهاد المنتظمة، N_eq (عند سعة 65% من إجهاد القص الدوري الأقصى، أي τ_cyc=0.65τ_max) التي من شأنها أن تنتج زيادة في ضغط المسام تعادل زيادة التاريخ الزمني غير المنتظم (الشكل 9.24). تم تطوير علاقات مماثلة لمستويات إجهاد أخرى (على سبيل المثال، Haldar and Tang، 1981) ولكن مستوى 65% هو الأكثر استخدامًا. في جميع الحالات، يزداد العدد المكافئ لدورات الإجهاد المنتظمة مع زيادة حجم الزلزال (تمامًا كما تزداد مدة الحركة القوية مع زيادة حجم الزلزال).

الشكل(9.24)

المثال الأول:

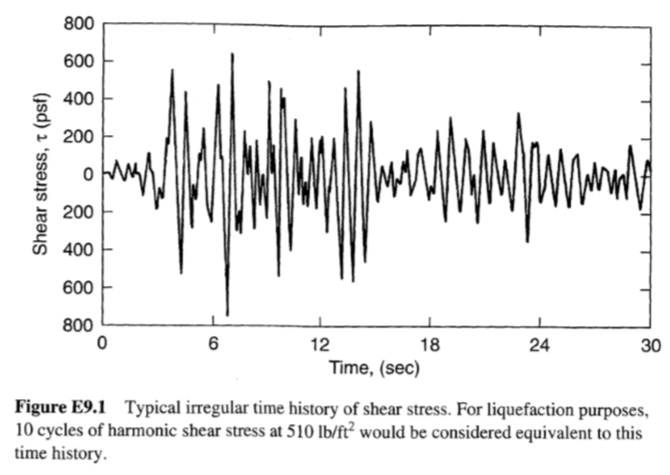
يوضح الشكل (1) سجلا زمنيا غير منتظم نموذجيًا لإجهاد القص الناتج عن زلزال بقوة M = 7.0. قم بتقدير سعة وعدد دورات التحميل لسلسلة مكافئة من دورات الإجهاد المنتظمة.

الحل: يوضح الشكل (1) أن أقصى إجهاد قص هو 780 رطل/قدم مربع lb/ft² (37.4 كيلو باسكال kPa). وبالتالي، فإن سعة السلسلة المكافئة لدورات الإجهاد المنتظمة هي:

τ_cyc=0.65τ_max=0.65*780=507 lb/ft²=24.3 kPa

بالإشارة إلى الشكل 9.24، فإن العدد المكافئ المقابل للدورات هو 10 تقريبًا.

يمكن أيضًا تقدير سعة إجهاد القص الدوري المنتظم للمواقع المستوية (أو المنحدرة بلطف) من إجراء مبسط (Seed and Idriss، 1971) على النحو التالي:

τ_cyc=0.65σ_vr_da_max/g

حيث a_max هو تسارع الأرض الأعظمي، وg تسارع الجاذبية، وσ_v الإجهاد الرأسي الكلي، وr_d قيمة عامل تقليل الإجهاد (الشكل 9.25) عند العمق المطلوب. يُفترض أن إجهاد القص الدوري المنتظم هذا يُطبق على العدد المكافئ من الدورات الموضحة في الشكل (9.24). وبغض النظر عما إذا كان يتم استخدام تحليل مفصل لاستجابة الأرض أو الإجراء المبسط، فإن التحميل الناتج عن الزلزال يتميز بمستوى من إجهاد القص الدوري المنتظم يُطبق على عدد مكافئ من الدورات.

الشكل(1)

الشكل(9.25)

المثال الثاني:

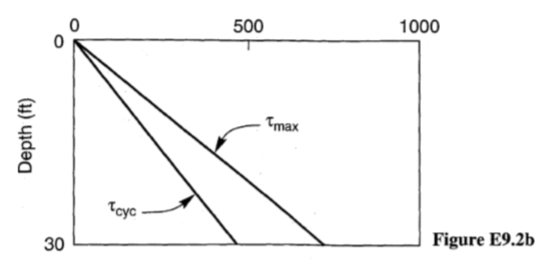
يتعرض الموقع الموضح في الشكل (2 a) لهزة زلزالية تنتج تسارعًا أرضيًا أقصى يبلغ 0.22g. قم بتقدير ورسم تباين إجهاد القص الأقصى مع العمق. احسب وارسم بيانيًا تغير إجهاد القص الدوري المنتظم المكافئ مع العمق.

الحل باستخدام الإجراء المبسط لسيد وإدريس (1971)، يمكن تقدير أقصى إجهاد قص من:

τ_max=σ_vr_da_max/g

يتطلب تقدير تغير τ_max مع العمق تقييم تغير إجمالي الإجهاد الرأسي σ_v وعامل تخفيض الإجهاد r_d مع العمق.

على أعماق 5 أقدام و25 قدمًا على سبيل المثال تكون الإجهادات الرأسية الكلية هي:

σ_v (z = 5 ft) = (5 ft)(105 Ib/ft³) = 525 1b/ft²

σ_v (z= 25 ft) = (10 ft)(105 lb/ft³) + (6 ft)(112 lb/ft³) + (9 ft)(71 lb/ft³ + 62.4 lb/ft³)= 2923 lb/ft²

على نفس الأعماق، يشير الشكل 9.25 إلى أن عامل تقليل الإجهاد:

r_d (z = 5 ft) = 0.992

r_d (z = 25 ft) = 0.947

يمكن بعد ذلك حساب أقصى إجهادات القص عند أعماق 5 أقدام و25 قدمًا يُعبر عنه على النحو التالي:

τ_max (z = 5 ft) = (0.22)(525 lb/ft²)(0.992) = 115 lb/ft²

τ_max (z = 25 ft) = (0.22)(2923 lb/ft²)(0.947) = 609 lb/ft²

تُؤخذ إجهادات القص الدورية المنتظمة المكافئة ببساطة على أنها 65% من إجهادات القص القصوى، أي:

τ_cyc (Z = 5 ft) = 75 lb/ft²

τ_cyc (Z = 25 ft) = 396 lb/ft²

من خلال تكرار هذه العملية لأعماق أخرى، يمكن تحديد الاختلافات في τ_max و τ_cyc ورسمها كما هو موضح في الشكل (2 b).

الشكل(2 a)

الشكل(2 b)

– توصيف مقاومة التميع:

تعتمد مقاومة التميع لعنصر من عناصر التربة على مدى قرب الحالة الأولية للتربة من الحالة المقابلة لـ “الفشل” وعلى طبيعة التحميل المطلوب لتحريكها من الحالة الأولية إلى حالة الفشل. ومع ذلك فإن حالة الفشل تختلف بالنسبة للتميع التدفقي والحركة الدورية. يمكن تعريف حالة الفشل للتميع التدفقي بسهولة باستخدام FLS، ويمكن التعرف على بدايتها بسهولة في الميدان. إن تعريف الفشل للحركة الدورية غير دقيق – قد يكون مستوى معين من التشوه الناجم عن الحركة الدورية مفرطًا في بعض المواقع ومقبولًا في مواقع أخرى. وعلى النقيض من التميع التدفقي، لا توجد نقطة مميزة يمكن عندها تعريف “فشل” الحركة الدورية. يُعتقد عمومًا أن فشل الحركة الدورية يحدث عندما تصبح ضغوط المسام كبيرة بما يكفي لإنتاج تذبذب أرضي أو انتشار جانبي أو دليل آخر على حدوث تلف على سطح الأرض. إن هذا التعريف للفشل غير دقيق؛ ففي الممارسة العملية، كثيراً ما يُنظر إلى وجود الغليان الرملي على أنه دليل على الحركة الدورية. ومع ذلك، فإن تطور الغليان الرملي لا يعتمد فقط على خصائص الرمل القابل للتحويل إلى سائل، بل وأيضاً على خصائص (مثل السُمك، والنفاذية، والسلامة) أي تربة فوقية. وفي الميدان، حيث نادراً ما يتم قياس الضغوط والإجهادات المسامية، غالباً ما يكون من الصعب التمييز بين ظواهر التميع المختلفة بعد وقوع الزلزال. وعندما تم تطوير نهج الإجهاد الدوري، لم يتم التمييز بين ظواهر التميع المختلفة ــ فقد تم جمع حالات التميع التدفقي والحركة الدورية معاً تحت العنوان العام “التميع”. وقد تم تطوير توصيف مقاومة التميع على طول خطين: الأساليب القائمة على نتائج الاختبارات المعملية، والأساليب القائمة على الاختبارات في الموقع وملاحظات سلوك التميع في الزلازل السابقة.

– التوصيف القائم على الاختبارات المعملية:

ركز التطوير المبكر لمنهج الإجهاد الدوري على الاختبارات المعملية لتوصيف مقاومة التميع. لإنشاء حالة أولية من الإجهاد المتراكم الصفري (لمحاكاة ظروف الإجهاد على المستويات الأفقية تحت الأرض المستوية)، تم إجراء معظم الاختبارات المعملية على عينات ثلاثية المحاور متماسكة بشكل متساوي الخواص أوعلى K₀ عينات قص بسيطة متماسكة. في هذه الاختبارات، تم تعريف “فشل التميع” عادةً على أنه النقطة التي تم عندها الوصول إلى التميع الأولي أو التي تم عندها الوصول إلى سعة إجهاد دوري محدودة (عادةً 5% للعينات الكثيفة). تُظهر الاختبارات المعملية أن عدد دورات التحميل المطلوبة لإنتاج فشل التميع N_L يتناقص مع زيادة سعة إجهاد القص ومع تناقص الكثافة (الشكل 9.26). في حين أن فشل التميع يمكن أن يحدث في بضع دورات فقط في عينة هشة معرضة لإجهادات قص دورية كبيرة، فقد تكون هناك حاجة إلى آلاف الدورات من إجهادات القص ذات السعة المنخفضة للتسبب في فشل التميع لعينة كثيفة. يمكن التعبير عن العلاقة بين الكثافة وسعة الإجهاد الدوري وعدد الدورات لفشل التميع بيانياً من خلال منحنيات القوة الدورية المعملية، مثل تلك الموضحة في الشكل (9.27). غالبًا ما يتم تطبيع منحنيات القوة الدورية بواسطة ضغط الحمل الزائد الفعال الأولي لإنتاج فشل دوري. نسبة الإجهاد (CSR). يجب تعريف نسبة الإجهاد بشكل مختلف لأنواع مختلفة من الاختبارات. بالنسبة لاختبار القص البسيط الدوري، يتم أخذ نسبة الإجهاد كنسبة إجهاد القص الدوري إلى الإجهاد الرأسي الفعال الأولي [أي، _ss=τ_cyc/σ’_v0(CSR)[ بالنسبة للاختبار الثلاثي المحاور الدوري، يتم أخذها كنسبة إجهاد القص الدوري الأقصى إلى ضغط الاحتواء الفعال الأولي ]أي؛ _tx=σ_dc/2σ’_3c(CSR)[ إن اختبارات القص البسيط الدوري والثلاثي المحاور الدوري تفرض حمولة مختلفة تمامًا، ونسب الإجهاد الدوري الخاصة بها ليست متكافئة. بالنسبة لاختبار التميع، عادة ما يرتبط الاثنان بـ:

_ss=c_r(CSR)_tx(CSR)

حيث يتم تقدير عامل التصحيح c_r من الجدول (1) وعلى النقيض من اختبارات القص البسيط الدوري والثلاثي المحوري الدوري في المختبر، فإن الزلازل تنتج إجهادات قص في اتجاهات مختلفة. وقد تبين أن الاهتزاز متعدد الاتجاهات (Pyke et al.,1975) يتسبب في زيادة ضغوط المسام بشكل أسرع من الاهتزاز أحادي الاتجاه. واقترح  Seed et al., 1975b))  أن نسبة CSR المطلوبة لإنتاج التميع الأولي في الحقل كانت أقل بنحو 10% من تلك المطلوبة في اختبارات القص البسيط الدوري أحادي الاتجاه. وبالتالي، فإن مقاومة التميع لعنصر من التربة في الحقل تعطى بنسبة الإجهاد الدوري:

(CSR)_field=τ_cyc/σ’_v0=0.9(CSR)_ss=0.9c_r(CSR)_tx

الشكل(9.26)

الشكل(9.27)

الجدول(1)

المثال الثالث:

طبقة سمكها مترين من رمل نهر ساكرامنتو (e = 0.87 وφ’ = 33^o) مغطاة بـ 4 أمتار من الحشو المضغوط (p_t = 2.1Mg/m³). يوجد منسوب المياه الجوفية في قاع الحشو. باستخدام نتائج اختبار ثلاثي المحاور الدوري الموضحة في الشكل 9.27، قم بتقدير أقصى إجهاد قص دوري مطلوب لبدء التميع في الرمال في زلزال بقوة 7.5 درجة. الحل الرمال تحت إجهاد رأسي فعال متوسط:

σ’_v0 = [(4 m)(2.1 Mg/m³)+(1.0 m)(0.91 Mg/m3)](9.81m/s²) = 91.3 kPa

وهو قريب من ضغوط الاحتجاز الفعالة لبيانات اختبار ثلاثي المحاور الدوري الموضحة في الشكل (9.27). باستخدام الشكل (9.24)، من المتوقع أن ينتج زلزال بقوة 7.5 درجة حوالي 14 دورة إجهاد موحدة (عند 65٪ من أقصى إجهاد قص). من الشكل (9.27)، فإن إجهاد الانحراف الدوري الذي من شأنه أن يسبب التميع الأولي في 14 دورة سيكون حوالي 39 كيلو باسكال. عندئذٍ تكون نسبة الإجهاد الدوري الثلاثي المحاور هي:

(CSR)_tx = σ_dc/2σ’_3c = 39 kPa/2(100 kPa)=0.195

يمكن تحديد نسبة الإجهاد الدوري الميداني المقابلة. بفرض أن K₀ = 1 – sinφ’ = 0.46. لدينا:

(CSR)_field = 0.9c_r(CSR)_tx = 0,9((1+0.46)/2)(0.195) = 0.128

عندئذٍ:

τ_cyc = (CSR)_fieldσ’_v0 = (0.128)(91.3) = 11.7 kPa

τ_max = τ_cyc/0.65 = 18.0 kPa

لذلك، ستكون هناك حاجة إلى إجهاد قص أعظمي يبلغ 18 كيلو باسكال لبدء التميع في رمال نهر ساكرامنتو في زلزال بقوة 7.5 درجة على مقياس ريختر.

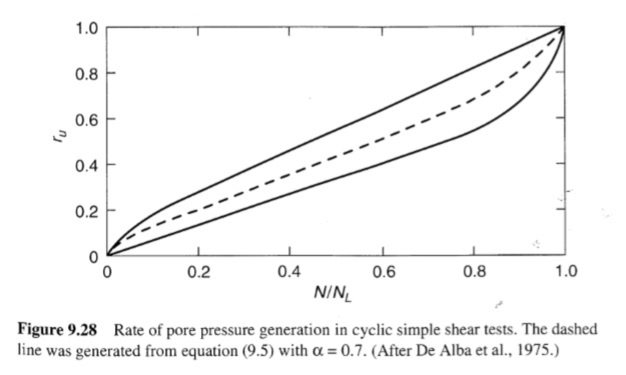
يمكن أن تكشف الاختبارات المعملية أيضًا عن الطريقة التي يتم بها توليد ضغط المسام الزائد. بالنسبة للاختبارات الدورية التي يتم التحكم فيها بالإجهاد مع التحميل المنتظم، وجد  Lee and Albaisa (1974) وDeAlba et al. (1975) أن نسبة ضغط المسام r_u مرتبطة بعدد دورات التحميل من خلال:

r_u = 1/2 + (1/π)sin^-1[2(N/N_L)^1/a-1]

حيث N_L هو عدد الدورات المطلوبة لإنتاج التميع الأولي (r_u = 1.00) وa هي دالة لخصائص التربة وظروف الاختبار. كما هو موضح في الشكل (9.28)، تزداد ضغوط المسام الزائدة بسرعة في دورات التحميل الأولى والأخيرة. يمكن استخدام المعادلة السابقة لتقدير ضغط المسام الزائد الناتج عندما لا يحدث التميع الأولي (أي عندما يكون N_eq < N_L). في نهج يمكن أن يعالج التحميل غير المنتظم، Martin et al. (1975) طور نموذجًا أساسيًا يجمع بين البيانات المتعلقة بمعدل ترسيب الرمال الجافة المحملة دوريًا مع البيانات المتعلقة بخصائص الارتداد والتشوه الإجهادي للتربة للتنبؤ بتوليد ضغط المسام. تم دمج النموذج في تحليلات استجابة الأرض غير الخطية لتوفير نهج فعال قائم على الإجهاد لتحليل التميع.

لعدة سنوات، كانت مقاومة التميع تتميز عادةً بالإجهادات الدورية التي يتم تحديدها من خلال الاختبارات المعملية. ومع ذلك، أظهرت الأعمال اللاحقة أن مقاييس مقاومة التميع القائمة على الإجهاد الدوري تتأثر بعوامل أخرى غير الكثافة الأولية وظروف الإجهاد. على سبيل المثال، تتأثر مقاومة التميع بالاختلافات في بنية التربة (أو نسيج التربة) الناتجة عن طرق مختلفة لإعداد العينة (Ladd, 1974; Mulilis et al., 1975; Toki et al., 1986; Tatsuoka et al., 1986) يؤثر تاريخ الإجهاد الزلزالي السابق أيضًا على مقاومة التميع [أي أن مقاومة التميع للعينة التي تعرضت لإجهاد زلزالي سابق تكون أكبر من مقاومة عينة بنفس الكثافة لم تتعرض لها (Finn et al., 1970; Seed et al., 1975b). كما تزداد مقاومة التميع مع زيادة نسبة التماسك الزائد ومعامل الضغط الأرضي الجانبي (Seed and Peacock, 1971). وأخيرًا، فقد تبين أن طول الوقت تحت الضغط المستمر (Ohsaki, 1969; Seed, 1979; Yoshimi et al., 1989) يزيد من مقاومة التميع. وهذه المعلمات الإضافية كلها وظائف للبيئة الترسيبية والتاريخية لرواسب التربة، وهي تميل إلى التأثير على سلوك التربة في المقام الأول عند مستويات الإجهاد المنخفضة المرتبطة ببدء التميع. ويمكن تدمير تأثيرات الإجهاد المنخفض هذه بسهولة عن طريق اضطراب أخذ العينات، ومن الصعب جدًا تكرارها في العينات المعاد تكوينها. وبسبب هذه العوامل، فإن تحديد خصائص مقاومة التميع من خلال الاختبارات المعملية أمر صعب للغاية وقد حلت محلها طرق تعتمد على نتائج الاختبارات في الموقع للعديد من المشاريع. إن أخذ العينات دون أي اضطراب حقيقي (على سبيل المثال، عن طريق تجميد الأرض بعناية وأخذ عينات من باطنها) مطلوب لإجراء الاختبارات المعملية حتى تتمكن من توصيف مقاومة التميع بشكل موثوق. كما يمكن أن تتعقد الاختبارات ثلاثية المحاور الدورية لمقاومة التميع بسبب عدم تجانس العينة. فمع تطور ضغوط المسام العالية في عينة اختبار ثلاثية المحاور دورية، تميل حبيبات التربة إلى الاستقرار مما يتسبب في تكثيف الجزء السفلي وتفكك الجزء العلوي من العينة. وتؤدي الكثافة غير المنتظمة إلى إجهاد غير منتظم، وفي النهاية إلى ترقق أو تضييق الجزء العلوي من العينة. ويمكن أن يتسبب عدم التجانس هذا في عدم يقين كبير في تطبيق نتائج الاختبار ثلاثية المحاور الدورية على الظروف الميدانية.

التوصيف بناءً على الاختبارات في الموقع:

هناك نهج بديل، وصفه Whitman لأول مرة (1971)، وهو استخدام حالات التميع لتوصيف مقاومة التميع من حيث معلمات الاختبار المقاسة في الموقع. يمكن وصف الحالات التاريخية السابقة من خلال الجمع بين معامل التحميل L ومعامل مقاومة التميع R والذي يمكن رسمه برمز يشير إلى ما إذا كان التميع قد تم ملاحظته أم لا (الشكل 9.29). ومن ثم يمكن رسم حدود بين تركيبات L-R التي أنتجت أو لم تنتج تميعًا في الزلازل السابقة. وعادة ما يتم رسم الحدود بشكل متحفظ بحيث تقع جميع الحالات التي لوحظ فيها التميع فوقها. وفي هذا النهج، تُستخدم نسبة الإجهاد الدوري عادةً كمعامل تحميل، وتُستخدم معلمات الاختبار في الموقع التي تعكس خصائص كثافة التربة وتوليد ضغط المسام كمعلمات مقاومة التميع.

1- مقاومة الاختراق القياسية: في الولايات المتحدة ومعظم البلدان الأخرى، كان اختبار الاختراق القياسي (SPT) هو الاختبار الأكثر استخدامًا في الموقع لوصف مقاومة التميع؛ والعوامل التي تميل إلى زيادة مقاومة التميع (مثل الكثافة، والإجهاد الزلزالي السابق، ونسبة التماسك الزائد، وضغوط الأرض الجانبية، والوقت تحت الضغط المستمر) تميل أيضًا إلى زيادة مقاومة SPT. قارن Seed et al. (1983) مقاومة SPT المصححة ونسبة الإجهاد الدوري لمواقع الرمل النظيف (الشكل 9.30) والرمل الطيني (الشكل 9.31) حيث لوحظ أو لم يلاحظ التميع في الزلازل التي تبلغ قوتها M = 7.5 لتحديد نسبة الإجهاد الدوري الأدنى التي يمكن توقع حدوث التميع عندها في رمل نظيف بمقاومة SPT معينة. إن وجود الإضافات يمكن أن يؤثر على مقاومة SPT وبالتالي يجب أن يؤخذ في الاعتبار في تقييم مقاومة التميع (Seed et al., 1985; Ishihara and Kosecki, 1989; Koester, 1994). يُظهر فحص الشكلين 9.30 و9.31 أن مقاومة التميع للرمال لا تتأثر بالإضافات إلا إذا كانت الإضافات تشكل أكثر من 5% من التربة. عند محتوى الإضافات الأعلى، تميل إلى تثبيط التميع [أي، CSR المطلوبة لبدء التميع (لقيمة ((N₁)₆₀ معينة)]. يمكن أن تؤثر مرونة الغراماتالإضافات أيضًا على مقاومة التميع؛ يميل التصاق الإضافات البلاستيكية إلى مقاومة الحركة النسبية لجزيئات التربة الفردية وبالتالي تقليل توليد ضغط المسام الزائد أثناء الزلازل. تشير الاختبارات المعملية (Ishihara and Koseki، 1989) إلى تأثير ضئيل عند مؤشرات اللدونة أقل من 10، وزيادة تدريجية في مقاومة التميع عند مؤشرات اللدونة أكبر من 10. اقترح Ishihara (1993) أن تأثيرات اللدونة يمكن تفسيرها بضرب نسبة CSR في العامل:

F=1.0 + 0.022(PI-10) عندما PI > 10

نظرًا لأن معظم الترب الرملية في الرواسب الرسوبية والحشوات من صنع الإنسان لها مؤشرات لدونة أقل من حوالي 15. فإن تأثير لدونة المواد الدقيقة يكون صغيرًا عادةً. نظرًا لأن مدة الحركة القوية (وبالتالي عدد مكافئ لدورات الإجهاد المنتظمة) تزداد مع شدة الزلزال، فإن الحد الأدنى لنسبة الإجهاد الدوري المطلوبة لبدء التميع يتناقص مع زيادة الشدة. يمكن الحصول على الحد الأدنى لنسبة الإجهاد الدوري لشدة أخرى عن طريق ضرب نسبة الإجهاد الدوري لزلزال بقوة M = 7.5 بالعوامل الموضحة في الجدول (2).

الشكل(9.28)

الشكل(9.29)

الجدول(2)

تتوافق البيانات التي تم تطوير الشكلين (9.30) و(9.31) منها في المقام الأول مع المواقع ذات الأرض المستوية ذات الرواسب الضحلة نسبيًا من التربة القابلة للتميع. في المواقع ذات الظروف الأرضية المنحدرة أو في المواقع التي تدعم الهياكل الثقيلة، فإن وجود إجهادات القص الساكنة الأولية سيؤثر على مقاومة التميع. في الظروف التي يكون فيها إجهاد القص الساكن أكبر من قوة الحالة المستقرة، تكون الظروف الأولية أقرب إلى FLS وتقل مقاومة التميع. تُظهر الاختبارات المعملية أن إجهاد القص الدوري المطلوب لتحفيز التميع يزداد عند ضغوط احتواء فعالة عالية. اقترح Seed (1983) أن يتم حساب تأثيرات إجهاد القص الأولي وضغوط الاحتواء الفعالة العالية عن طريق تعديل نسبة الإجهاد الدوري على النحو التالي:

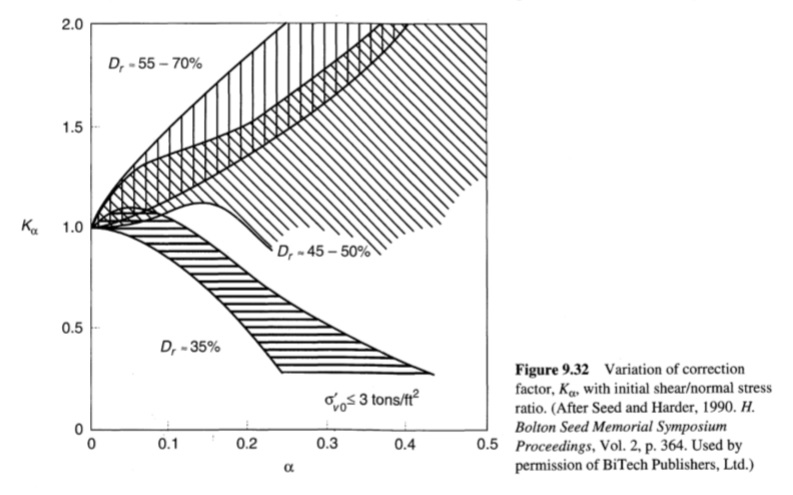
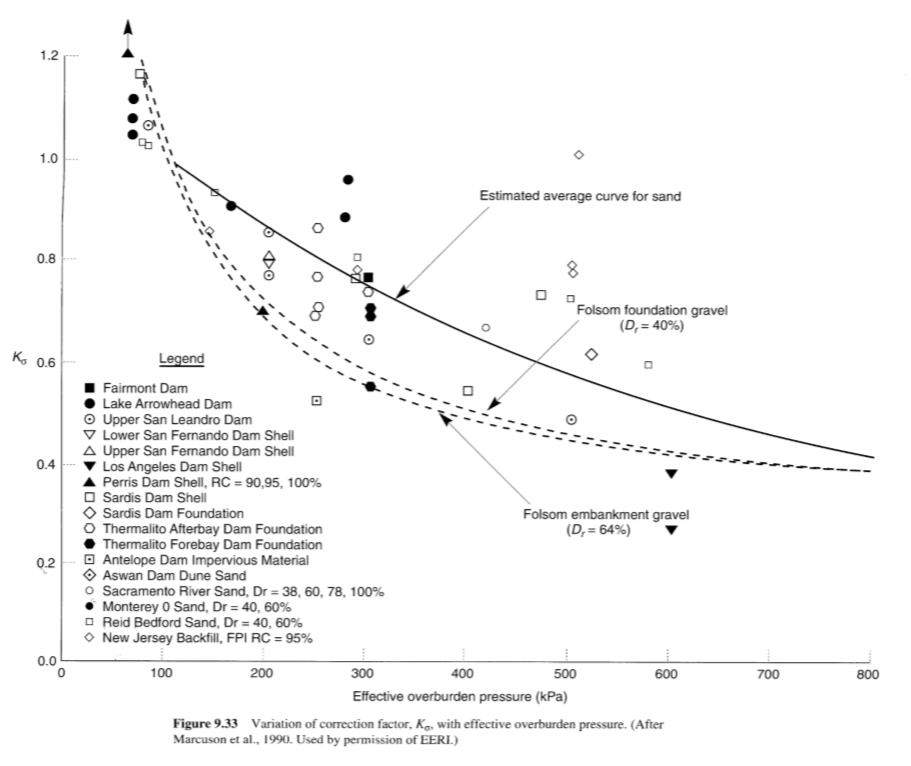
(CSR_field)_{a, σ} = (CSR_field)_{a=0, σ < 1 ton/ft2}K_aK_σ

حيث a= τ_{h, static}/σ’_v0 وK_a وK_σ هي عوامل تصحيح لإجهاد القص الأولي (الشكل 9.32) وضغط الحمل الزائد الفعال (الشكل 9.33) على التوالي. تختلف قيم K_a وK_σ باختلاف التربة ويجب تقييمها على أساس خاص بالموقع كلما أمكن ذلك.

الشكل(9.30)

الشكل(9.31)

الشكل(9.32)

الشكل(9.33)

2- مقاومة الاختراق:

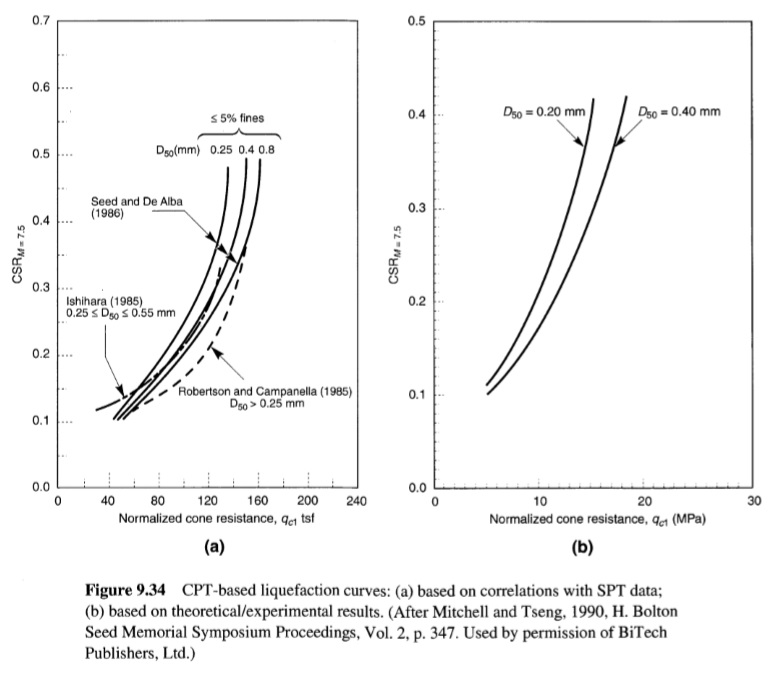
يمكن أيضًا استخدام (CPT) كمقياس لمقاومة التميع، والتي تتمتع بميزة واضحة في قدرتها على اكتشاف طبقات رقيقة من التربة الرخوة. قاعدة بيانات المواقع التي تم فيها قياس مقاومة CPT وحيث تم توثيق حدوث أو عدم حدوث التميع، على الرغم من نموها السريع، تظل صغيرة إلى حد ما. من خلال استكمال هذه البيانات بالارتباطات بين مقاومات CPT وSPT، يمكن تحديد نسبة الإجهاد الدورية الدنيا التي يمكن توقع التميع عندها في رمل نظيف بمقاومة CPT معينة (Robertson and Campanella, 1985; Seed and DeAlba, 1986). نظرًا لأن ارتباط CPT-SPT يعتمد على حجم الحبيبات، فقد تم تطوير منحنيات التميع القائمة على CPT لأحجام حبيبات متوسطة مختلفة (الشكل 9.34 a). قام Mitchell and Tseng (1990) بتطوير منحنيات تعتمد على الاختبارات المعملية والقيم المشتقة نظريًا لمقاومة CPT (الشكل 9.34 b). إن ارتباط CPT-SPT الذي يستخدم نسبة الاحتكاك (Douglas et al., 1981; Martin, 1992) يلغي الحاجة إلى قياس متوسط ​​حجم الحبيبات (والحفر وأخذ العينات المطلوبة للقيام بذلك). في تقييمات التميع القائمة على CPT، يتم تطبيق المقاومة إلى ضغط الحمل الزائد الفعال القياسي البالغ 1 طن/قدم2 (96 كيلو باسكال) من خلال:

q_{c 1} = q_c(P_a/σ’_v0)^0.5

q_{c 1} = q_c(1.8/0.8 + σ’_v0)

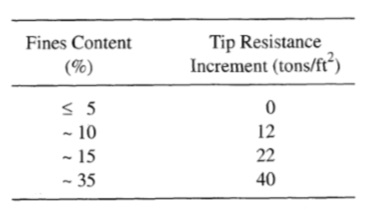
حيث: σ’_v0 بالطن/القدم المربع (Kayen et al., 1992). يمكن إجراء التعديل لمقادير أخرى غير 7.5 باستخدام عوامل تصحيح CSR المقدمة في الجدول 9-2. Kayen et al. (1992) وجد أن ملاحظات التميع في زلزال لوما بريتا عام 1989 تتفق بشكل جيد مع منحنيات Robertson and Campanella (1985) وMitchell and Tseng (1990). بالنسبة للرمال الطينية يمكن إضافة الزيادات في الجدول(3) للحصول على مقاومة رمل نظيف مكافئة (Ishihara، 1993).

الشكل(9.34)

الجدول(3)

3- سرعة موجة القص:

ساهمت الأساليب المحسنة لقياس سرعة موجة القص في الموقع والدراسات المتعلقة بتطوير نهج الإجهاد الدوري في الاعتراف بسرعة موجة القص كمقياس مفيد لمقاومة التميع. يمكن تطبيع سرعات موجة القص المقاسة إلى ضغط الحمل الزائد الفعال القياسي البالغ 1 طن / قدم مربع (96 كيلو باسكال) بواسطة:

v_s1=v_s(σ’_v0)^-1/n

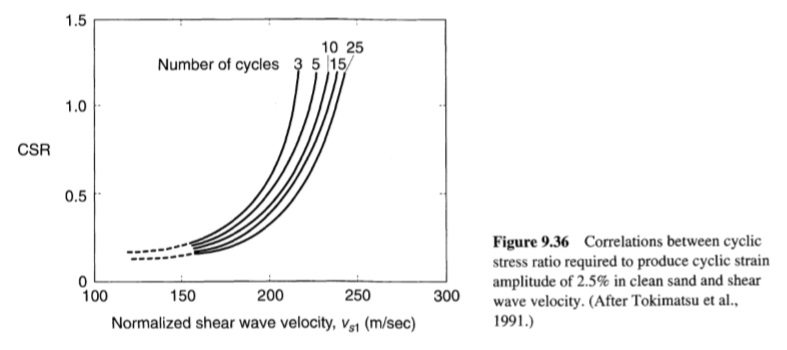
حيث σ’_v0 بالطن/القدم المربع وتم اعتبار n=3 (Tokimatsu et al.,1991)أو 4 (Finn, 1991؛ Kayen et al., 1992) استخدم Stokoe et al. (1988) نهج الانفعال الدوري وتحليلات الاستجابة الأرضية الخطية المكافئة لاستكشاف العلاقة بين تسارع سطح الأرض الأعظمي (لظروف موقع التربة الصلبة) وسرعة موجة القص. تم استخدام النتائج لتطوير حدود للظروف التي يمكن توقع التميع فيها؛ تتفق النتائج جيدًا مع السلوك الملحوظ في زلزالين في إمبريال فالي في كاليفورنيا (الشكل 9.35). استخدم Tokimatsu et al. (1991) نتائج الاختبارات المعملية لتطوير منحنيات توضح CSR المطلوبة لإنتاج سعة إجهاد دوري تبلغ 2.5% في أعداد مختلفة من الدورات كدالة لسرعة موجة القص المصححة (الشكل 9.36). إن الملاحظة التي تفيد بأن سرعة موجة القص للرمل غير حساسة لعوامل (مثل نسيج التربة، ونسبة التماسك الزائد، والإجهاد الدوري السابق) المعروف أنها تؤثر على مقاومة التميع تشير إلى أن قياسات سرعة موجة القص وحدها قد لا تكون كافية لتقييم إمكانية التميع لجميع رواسب التربة (Jamiolkowsky and LoPresti, 1992; Verdugo, 1992).

الشكل(9.25)

الشكل(9.36)

4- مؤشر التمدد:

تم اقتراح ارتباطات لإمكانية التميع مع مؤشر الإجهاد الأفقي لاختبار مقياس التمدد (DMT) أيضا (Marchetti, 1982; Robertson and Camponella, 1986; Reyna and Chameau, 1991). يوضح الشكل (9.37) أداء ثلاثة من هذه الارتباطات عند تطبيقها على بيانات من عدة مواقع في كاليفورنيا. يجب توقع ارتباطات جديدة لمؤشر DMT مع اكتساب خبرة إضافية مع هذا الاختبار الجديد نسبيًا في الموقع.

الشكل(9.37)

5- استخدام نتائج الاختبار في الموقع:

إن مقاومة SPT هي أكثر معلمات الاختبار في الموقع استخدامًا لتوصيف مقاومة التميع. تسمح SPT باسترجاع العينة ولديها أكبر قاعدة بيانات لتاريخ الحالات لأي اختبار في الموقع. ومع ذلك، أصبحت CPT تستخدم بشكل أكثر شيوعًا لتوصيف مقاومة التميع. توفر CPT سجلاً مستمرًا لمقاومة الاختراق وهي أسرع بكثير وأقل تكلفة من SPT. نظرًا لأن مقاومة التميع المستندة إلى CPT تتأثر بخصائص حجم الحبيبات (الشكل 9.34)، فقد تكون هناك حاجة إلى عمليات حفر تكميلية مع أخذ العينات.

بغض النظر عن الطريقة المستخدمة، تسمح معلمات الاختبار في الموقع بتقدير نسبة إجهاد القص الدوري المطلوبة لبدء التميع. باستخدام تعريف نسبة الإجهاد الدوري، يتم تحديد إجهاد القص الدوري المطلوب لبدء التميع من خلال:

Τ_cyc,L = CSR_Lσ’_v0

تقييم بدء التميع:

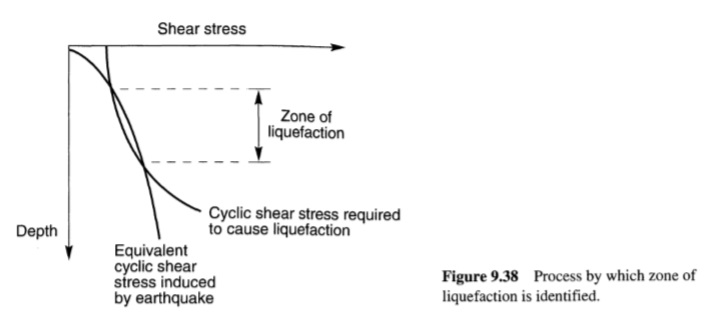
بمجرد تحديد الحمل الدوري المفروض من قبل الزلزال ومقاومة التميع للتربة، يمكن تقييم إمكانية التميع. يميز نهج الإجهاد الدوري تحميل الزلزال بسعة الإجهاد الدوري المنتظم المكافئ ومقاومة التميع بسعة الإجهاد الدوري المنتظم المطلوب لإنتاج التميع في نفس عدد الدورات. وبالتالي يتم تقليل تقييم إمكانية التميع إلى مقارنة التحميل والمقاومة في جميع أنحاء رواسب التربة ذات الاهتمام. يتم إجراء التقييم بسهولة بيانياً. أولاً، يتم رسم تغير إجهاد القص الدوري المكافئ (تحميل الزلزال، τ_cyc)، مع العمق كما هو موضح في الشكل (9.38) (يجب تحديد عدد الدورات المكافئة، N_eq، المقابلة لحجم الزلزال إذا كان من المقرر وصف مقاومة التميع باستخدام نتائج الاختبارات المعملية). ثم يتم رسم تغير إجهاد القص الدوري المطلوب للتسبب في التميع (مقاومة التميع، _cyc,Lτ) مع العمق على نفس الرسم البياني (يجب أن تتوافق قيم _cyc,Lτ مع نفس حجم الزلزال، أو نفس عدد الدورات المكافئة، مثل τ_cyc). يمكن توقع التميع عند الأعماق حيث يتجاوز التحميل المقاومة أوعندما يكون عامل الأمان ضد التميع، المعبر عنه بـ:

FS_L= cyclic shear stress required to cause liquefaction/ equivalent cyclic shear stress induced by earthquake= τ_cyc,L/τ_cyc= CSR_L/CSR

أقل من 1.

ويجب ملاحظة أنه يمكن أن يتطور ضغط مسام زائد كبير حتى إذا كان عامل الأمان المحسوب أكبر من 1. في المواقع ذات الأرض المستوية، على سبيل المثال، يمكن تقدير حجم ضغط المسام الزائد هذا من الشكل (9.39). يمكن أن يؤدي الانخفاض في الإجهاد الفعال المرتبط بضغوط المسام الزائدة هذه إلى تقليل صلابة التربة، ويمكن أن يحدث ترسيب كبير مع تبدد ضغوط المسام الزائدة.

الشكل(9.38)

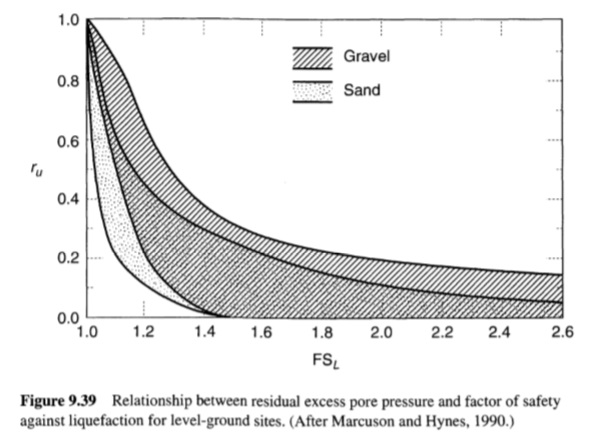
الشكل(9.39)

المثال الرابع:

تم وصف موقع في اليابان وتم إجراء اختبارات SPT في الموقع باستخدام تقنيات SPT اليابانية القياسية؛ وقد تم وصف العملية التي يتم من خلالها تصحيح مقاومات SPT المقاسة للحصول على قيم (N₁)₆₀، حدد المدى الذي كان من المتوقع حدوث التميع فيه في زلزال نيجاتا عام 1964 (M = 7.5) إذا كان التسارع الأرضي الأعظمي عند سطح الأرض g0.16.

الحل يتضمن تقييم إمكانية التميع من خلال نهج الإجهاد الدوري مقارنة مستوى الإجهاد الدوري الناجم عن الزلزال بمستوى الإجهاد الدوري المطلوب لبدء التميع. يمكن تقدير مستوى الإجهاد الدوري الناجم عن الزلزال من المعلومات المتاحة باستخدام الإجراء المبسط Seed and Idriss (1971). يمكن حساب تغير الإجهاد الرأسي الكلي مع العمق بسهولة. على سبيل المثال، يتم إعطاء الإجهاد الرأسي الكلي عند عمق 6.2 متر بواسطة:

σ_v0 = (1.5 m)(1.874Mg/m³) + (4.7m)(2.180Mg/m³)(9.81m/s²) = 128.1 kPa

يمكن الحصول على قيمة عامل تقليل الإجهاد بيانياً من الشكل (9.25). على عمق 6.2 متر، rd = 0.960. بمعرفة التسارع الأعظمي، يتم حساب إجهاد القص الدوري على عمق 6.2 متر،

_cyc=0.65(0.16g/g)(128.1 kPa)(0.960) =12.8 kPaτ

يعتمد مستوى إجهاد القص الدوري المطلوب لبدء التميع على مقاومة التميع للتربة. في هذا المثال، يمكن وصف مقاومة التميع بقيم ₆₀(N₁). باستخدام الرسم البياني في الشكل 9.31، يمكن إيجاد نسب الإجهاد الدوري المطلوبة لبدء التميع بيانياً. على عمق 6.2 متر، تتوافق القيمة ₆₀=11.7(N₁) مع CSR_M=7.5 = 0.130. ولأن شدة زلزال نيغاتا كانت 7.5، فإن معامل تصحيح الشدة له بقيمة 1.0. وعندئذٍ

CSR_L = (CSR_M=7.5)(1.0) = 0.130

بمعرفة CSR_L وتغير الإجهاد الرأسي الفعال مع العمق، يمكن حساب الإجهاد الدوري المطلوب لبدء التميع (الشكل 4 a). على عمق 6.2 متر،

τ_cyc,L=CSR_Lσ’_v0=0.130(82.0 kPa)=10.7 kPa

وأخيرًا، يمكن مقارنة الإجهاد الدوري الناتج عن الزلزال بالإجهاد الدوري المطلوب لبدء التميع. باستخدام مفهوم عامل الأمان ضد التميع، ويمكن تحديد تغير عامل الأمان مع العمق (الشكل 4 b) على عمق 6.2 متر،

FS_L=τ_cyc,L/τ_cyc=10.7/12.8=0.84

كما هو موضح في (الجدول 9.3 والشكل 4 b)، فإن عامل الأمان ضد التميع أكبر من ذلك الذي يكون فيه الإجهاد الدوري الناتج عن الزلزال أقل من الإجهاد الدوري المطلوب لبدء التميع (τ_cyc<τ_cyc,L). في هذا الموقع، كان من المتوقع حدوث تميع واسع النطاق في الجزء العلوي من 8 إلى 10 أمتار وفي بعض الأعماق الأكبر أيضًا. إن ظروف هذا المثال تمثل تلك الموجودة في منطقة كاواجيشي-تشو في نيجاتا، اليابان على الرغم من أن تسارع الذروة الفعلي ربما كان في حدود 0.2 إلى 0.3g. إن التميع الواسع النطاق المتوقع في هذا المثال يتوافق مع ما لوحظ بالفعل في تلك المنطقة في زلزال نيجاتا عام 1964.

لأن النسب، CSR وCSR_L، ​​يختلفان على مدى أصغر كثيرًا من إجهادات القص الدورية نفسها.

نهج الإجهاد الدوري:

إن العدد الكبير من العوامل التي تؤثر على الإجهادات الدورية المطلوبة لإنتاج التميع يمكن أن يجعل التقييم المختبري لمقاومة التميع في نهج الإجهاد الدوري صعبًا. وكما أشار Seed (1976)، “يتم تحديد خصائص التميع لرواسب الرمل في الموقع من خلال عدد من العوامل المعقدة، والتي تعد الكثافة النسبية أحدها فقط، والتقييمات الدقيقة لجميع هذه العوامل مطلوبة في اختيار خصائص التربة لاستخدامها في التصميم”. في محاولة لتطوير نهج أكثر قوة لمشكلة التميع، وصف  Dobry and Ladd (1980) وDobry et al. (1982) نهجًا يستخدم الإجهادات الدورية لتوصيف التحميل ومقاومة التميع الناجم عن الزلازل. يعتمد النهج على الأدلة التجريبية التي تظهر أن تكثيف الرمال الجافة يتم التحكم فيه بواسطة إجهادات دورية (على سبيل المثال، Silver and Seed, 1971، ؛ Youd, 1972) ووجود إجهاد القص الحجمي العتبي الذي لا يحدث التكثيف تحته. نظرًا لأن ميل الرمل إلى التكثيف عندما يكون جافًا يرتبط ارتباطًا مباشرًا بميله إلى تطوير ضغط مسام زائد عند التشبع، فمن الطبيعي أن يكون توليد ضغط المسام مرتبطًا بشكل أكثر جوهرية بالإجهادات الدورية.

توصيف ظروف التحميل:

في نهج الإجهاد الدوري، يتم التعبير عن التحميل الناجم عن الزلزال من حيث الإجهادات الدورية. التاريخ الزمني للإجهاد الدوري في زلزال فعلي عابر وغير منتظم. لمقارنة التحميل بمقاومة التميع المقاسة في المختبر، يجب تمثيله بسلسلة مكافئة من دورات الإجهاد المنتظمة. إجراء التحويل مماثل لذلك المستخدم في نهج الإجهاد الدوري. يمكن حساب التاريخ الزمني لإجهاد القص الدوري في تحليل استجابة الأرض. ربما يكون هذا هو الحلقة الأضعف في نهج الإجهاد الدوري حيث يصعب التنبؤ بالإجهادات الدورية بدقة أكثر من الإجهادات الدورية (Seed,1980). اقترح Dobry et al. (1982) طريقة مبسطة لتقدير سعة الإجهاد الدوري المنتظم:

_cyc = 0.65(a_max/g)(σ_vr_d/G(ϒ_cyc))ϒ

حيث G(ϒ_cyc) هي معامل القص للتربة عند =ϒ_cycϒ. نظرًا لأن ϒ_cyc يؤثر على جانبي المعادلة، فيجب الحصول على قيمة G(ϒ_cyc) بشكل تكراري من ملف تعريف G_max المقاس ومنحنيات تخفيض معامل القص المناسبة. يعتمد العدد المكافئ لدورات الانفعال N_eq على حجم الزلزال، ويمكن تقديره من الشكل (9.24). بمجرد تحديد ϒ_cyc يمكن مقارنته بإجهاد القص العتبي ϒ_t. إذا كان ϒ_cyc<ϒ_t فلن يتم إنشاء أي مسام وبالتالي لا يمكن بدء التميع. سينتهي تقييم مخاطر التميع عند هذه النقطة. إذا كان ϒ_cyc>ϒ_t يكون التميع ممكنًا ويجب تقييم مقاومة التميع للتربة.

توصيف مقاومة التميع:

يبسط نهج الإجهاد الدوري تفسير مقاومة التميع من الاختبارات المعملية. تشير الأدلة التجريبية إلى أن العوامل التي تزيد من الضغوط الدورية المطلوبة لبدء التميع (على سبيل المثال، الكثافة، ونسيج التربة، وتاريخ الانفعال، ونسبة التماسك الزائد، وطول الوقت تحت الضغط المستمر) تزيد أيضًا من معامل القص للتربة. نظرًا لأن هذه العوامل تؤثر على كل من τ_cyc وG على نحو مماثل، فإن تأثيرها على النسبة _cyc=τ_cyc/Gϒ أصغر كثيرًا. وبالتالي، فإن تأثيرها على توليد ضغط المسام ضئيل عند تفسيره من حيث الانفعالات الدورية. قدم  Dobry and Ladd (1980) دليلاً مذهلاً على هذه النتيجة؛ يوضح الشكل (9.40) نسبة ضغط المسام الناتجة عن 10 دورات تحميل يتم التحكم فيها بالانفعال على رمال مختلفة تم تحضيرها بثلاث طرق مختلفة عند ثلاثة ضغوط احتواء فعالة أولية مختلفة. إن عدم حساسية ضغط المسام الناتج لعوامل أخرى غير سعة الانفعال الدوري الموضحة في الشكل (9.40) هي السمة المميزة لنهج الانفعال الدوري.

طور Dobry et al (1984) اختبارًا ثلاثي المحاور مبتكرًا يسمى اختبار CyT-CAU لقياس مقاومة التميع. في هذا الاختبار، يتم توحيد عينة أسطوانية صلبة ثلاثية المحاور بشكل متباين الخواص تحت إجهاد انحراف ثابت يتم التحكم فيه بالإجهاد. ثم يتم فرض إجهادات دورية في ظل ظروف غير مستنزفة بواسطة الالتواء الدوري الذي يتم التحكم فيه بالإجهاد بينما يظل إجهاد الانحراف الذي يتم التحكم فيه بالإجهاد ثابتًا. تسبب إجهادات القص الدورية ضغطًا زائدًا للمسام في العينة. إذا وصلت ظروف الإجهاد الفعالة إلى FLS وكانت قوة الحالة المستقرة أقل من إجهاد القص الثابت، فسيحدث تميع التدفق. يحاكي هذا الاختبار عن كثب سلوك التربة التي تتعرض لتيسير التدفق في الحقل: يتم توليد ضغوط المسام الزائدة بواسطة إجهادات القص الدورية، ولكن فشل التدفق مدفوع بإجهادات القص الثابتة. استخدم Vasquez-Herrera and Dobry (1988) اختبار CyT-CAU للتحقيق في توليد ضغط المسام الزائد وبدء التميع التدفقي. وتأكيدًا لوجود FLS للعديد من الرمال، لاحظا أيضًا أن ضغط المسام الزائد المطلوب لتحفيز التميع انخفض مع زيادة نسبة الإجهاد الفعال الرئيسي الأولي، وانخفاض مماثل في عدد دورات الانفعال المطلوبة لتحفيز التميع (الشكل 9.41). يمكن التعبير عن سعة الانفعال الدوري المطلوبة لتحفيز التميع في دورات N_eq في الشكل:

ϒ_cyc =0.01(r_u,t/aN_eq(2-r_u,t))^1/β

حيث a و β هما دالتان محددتان تجريبيًا لـ K_c تستخدمان لتوصيف مقاومة التميع في نهج الانفعال الدوري. يتأثر المعدل الذي تتطور به ضغوط المسام الزائدة أيضًا بـ K_c؛ تزداد ضغوط المسام الطبيعية بشكل أسرع في الدورات الأولى للعينات عند قيم K_c المنخفضة (الشكل 9.42).

تقييم جهد التميع:

يمكن تقييم جهد التميع في طريقة الإجهاد الدوري بطريقة مماثلة لتلك المستخدمة في طريقة الإجهاد الدوري. تتم مقارنة الدورية التي يفرضها الزلزال، والتي تتميز بسعة سلسلة من دورات الإجهاد المنتظمة N_eq، بمقاومة التميع، والتي يتم التعبير عنها من حيث سعة الإجهاد الدوري المطلوبة لبدء التميع في نفس عدد الدورات. يمكن توقع التميع عند الأعماق حيث يتجاوز التحميل الدوري مقاومة التميع (الشكل 9.43). نظرًا لأن التحميل والمقاومة يتميزان من حيث الإجهادات، فإن طريقة الإجهاد الدوري لا تعطي عامل أمان ضد التميع.

الميزة الأساسية لمنهج الإجهاد الدوري تنبع من العلاقة القوية بين توليد ضغط المسام وسعة الإجهاد الدوري. بالنسبة لتربة معينة، يمكن التنبؤ بضغط المسام الزائد بدقة أكبر من الإجهادات الدورية. ومع ذلك، فإن الإجهادات الدورية يصعب التنبؤ بها بدقة. لا يتم استخدام منهج الإجهاد الدوري بشكل شائع في ممارسة هندسة الزلازل الجيوتقنية.

مناهج أخرى لبدء التميع:

على الرغم من أن مناهج الإجهاد الدوري هي الأكثر استخدامًا في ممارسة هندسة الزلازل الجيوتقنية، فقد تم تطوير مناهج أخرى أيضًا. اثنان يقدمان وعدًا كبيرًا هما منهج الطاقة المبددة ومنهج تحليل الاستجابة القائم على الإجهاد الفعال. مع تحسين هذه المناهج، ومع توفر البيانات الإضافية لمعايرتها، من المرجح أن يزداد استخدامها.

منهج تبديد الطاقة:

إن استخدام الطاقة المبددة كمقياس لمقاومة التميع يوفر عددًا من المزايا؛ فهي مرتبطة بكل من الإجهادات الدورية والانفعالات الدورية، ويمكن ربطها بحركات الأرض الزلزالية العشوائية بطبيعتها بطريقة لا تستطيع الأساليب القائمة على معلمات حركة الأرض القصوى وحدها القيام بها، فهي كمية قياسية، ويمكن ربطها بمعلمات الزلزال الأساسية. تتضمن تكثيف التربة الجافة إعادة ترتيب الحبيبات وبالتالي إنفاق الطاقة. مع تكثيف التربة الجافة المحملة دوريًا واقترابها من نسبة الفراغ الدنيا، تزداد كمية الطاقة المطلوبة لإعادة ترتيب حبيبات التربة الفردية. ومع ذلك، بالنسبة للتربة المشبعة، يتسبب ميل التكثيف في زيادة ضغط المسام وانخفاض قوى التلامس بين الجسيمات. ومع انخفاض قوى التلامس هذه، تقل كمية الطاقة اللازمة لإعادة ترتيب حبيبات التربة. من خلال الجمع بين هذه الملاحظات، طور Nemat-Nasser and Shokooh (1979) نظرية بسيطة وموحدة تربط بين التكثيف في ظل الظروف المجففة وتوليد ضغط المسام في ظل الظروف غير المجففة والطاقة المبددة. حاول آخرون منذ ذلك الحين توصيف العلاقة بين ضغط المسام الزائد والطاقة المبددة تجريبياً (على سبيل المثال،  Simcock et al، 1983؛ Law et al، 1990؛ Figueroa and Dahisaria، 1991). وعلى الرغم من أن بعض البيانات متناثرة تمامًا، إلا أنه يمكن التنبؤ بضغط المسام الزائد من خلال علاقة من النموذج:

Δu/σ’v0=aW_N^β

حيث W_N هو مصطلح طاقة بلا أبعاد (Law et al، 1990) وa وβ هما معاملات تم تحديدها من الاختبارات المعملية. أظهرDavis and Berrill (1982) إمكانية استخدام الطاقة لربط سلوك التميع بمعلمات الزلزال الأساسية مثل القدر والمسافة. من خلال الجمع بين تقدير محتوى الطاقة في الموجات الزلزالية على مسافة R من زلزال بقوة M مع دالة تبديد الطاقة البسيطة التي تم معايرتها من خلال النتائج التجريبية والملاحظات الميدانية لسلوك التميع، تم تطوير تعبير للضغط الزائد في المسام.

Δu=(450*10^1.5M)(R²*N1²*σ’_v0^-1)

حيث R هي بالأمتار، وN₁ هي مقاومة SPT المصححة إلى ضغط حمل زائد فعال يبلغ 1 طن/قدم مربع (96 كيلو باسكال)، و Δu و σ’_v0 بالكيلو باسكال. استخدم Law et al (1990) مبادئ الطاقة لتطوير المعيار التالي لفشل التميع في الرمال:

101.5M/(2.28*10^-10*N1^11.5*R^4.3)>=1

حيث R هي المسافة تحت المركزية بالكيلومتر.

نهج تحليل الاستجابة القائم على الإجهاد الفعال:

كان نمذجة الإجهاد والانفعال لسلوك التربة موضوعًا لنشاط بحثي مكثف لسنوات عديدة، وقد ثبت أن مهمة تكرار السلوك المعقد للتربة القابلة للتميع باستخدام نماذج تكوينية بسيطة صعبة. يمكن وصف سلوك الإجهاد والانفعال غير الخطي للتربة من خلال نماذج الإجهاد والانفعال غير الخطية الدورية والنماذج التكوينية المتقدمة. تستخدم نماذج الإجهاد والانفعال غير الخطية الدورية منحنى العمود الفقري التجريبي وسلسلة من قواعد التفريغ وإعادة التحميل التي تحكم السلوك الدوري. يتم إنجاز التنبؤ بضغط المسام من خلال نماذج ضغط المسام (على سبيل المثال، Martin et al.، 1975؛ Ishihara and Towhata، 1980؛ Finn and Bhatia، 1981) التي يمكنها التنبؤ بتوليد ضغط المسام في ظل ظروف تحميل دورية غير منتظمة. يتم استخدام ضغط المسام المحسوب لتدهور أو تليين منحنى العمود الفقري مع انخفاض الإجهاد الفعال (وصلابة التربة). في نموذج Martin et al. (1975) ، على سبيل المثال، يرتبط ضغط المسام الناتج عن زيادة التحميل غير المصرف بالإجهاد الحجمي الذي كان ليحدث في نفس زيادة التحميل في ظل ظروف الصرف من خلال:

u = E_rΔε_vdΔ

حيث E_r، هو معامل الارتداد وΔε_vd هو الإجهاد الحجمي المتزايد في ظل ظروف الصرف. يمكن التعبير عن معامل الارتداد على النحو التالي:

E_r=(σ’_v)^1-m/(m K₂ (σ’_v0)^n-m)

حيث ‘_vσ وσ’_v0 هما الإجهادان الرأسيان الفعالان الحاليان والأوليان ويتم تحديد m وn وK₂ تجريبيًا من اختبار الارتداد في مقياس الصلابة. يتم حساب الانفعال الحجمي المتزايد على النحو التالي:

Δε_vd=C₁(ϒ-C₂ε_vd)+C₃ε_vd²/(ϒ+C₄ε_vd)

حيث ϒ و ε_vdهما القص الدوري والانفعالات الحجمية على التوالي، وC1-C4 هي ثوابت يتم تحديدها من نتائج اختبارات القص الدوري البسيط المفرغة. طور Martin et al (1981) إجراءً لتقدير هذه الثوابت دون نتائج اختبار معملية. عند دمجها في تحليلات استجابة الأرض غير الخطية، تسمح نماذج الضغط غير الخطي الدوري وضغط المسام بحساب توليد وإعادة توزيع وتبديد ضغوط المسام. وبالتالي يمكن مراقبة ظروف الإجهاد الفعال في جميع أنحاء رواسب التربة طوال الزلزال وحتى بعده لتقييم مخاطر التميع.

تقدم النماذج التكوينية المتقدمة نهجًا أكثر صرامة للتنبؤ بسلوك التربة في ظل مجموعة واسعة من ظروف التحميل. تصف مثل هذه النماذج الزيادات في الإجهاد الحجمي والانحرافي الناتج عن زيادات الإجهاد الحجمي والانحرافي. من خلال ضبط الإجهاد الحجمي المتزايد على الصفر لتمثيل الظروف غير المصرفة، يمكن حساب التغيرات في الإجهادات الفعالة. يمكن دمج مثل هذه النماذج في تحليلات الاستجابة الأرضية غير الخطية والاستجابة الديناميكية. على سبيل المثال، يستخدم برنامج الاستجابة الأرضية غير الخطية أحادي البعد DYNAlD (Prevost, 1989)، نموذج تكويني لسطح الخضوع المتداخل لتفسير سلوك التربة غير الخطي والمتباين الخواص والهستيري للتنبؤ بتوليد وإعادة توزيع وتبديد ضغط المسام الزائد أثناء وبعد اهتزاز الزلزال.

النهج الاحتمالي:

هناك العديد من المصادر المحتملة لعدم اليقين في كل من جوانب التحميل والمقاومة لمشاكل التميع، وقد تم تطوير مناهج احتمالية للتعامل معها. يمكن تقييم عدم اليقين في التحميل الدوري باستخدام تحليلات المخاطر الزلزالية الاحتمالية القياسية. يمكن معالجة عدم اليقين في مقاومة التميع بإحدى طريقتين عامتين. تعتمد إحدى مجموعات الطرق على التوصيف الاحتمالي للمعلمات التي تظهرها الاختبارات المعملية للتأثير على توليد ضغط المسام. وصف Haldar and Tang (1979) عدم اليقين في معلمات نهج الإجهاد الدوري المبسّط، استخدم Fardis and Veneziano (1982) نهجًا مشابهًا مع نماذج الإجهاد الكلي والإجهاد الفعال. وصف Chameau and Clough (1983) توليد ضغط المسام بشكل احتمالي باستخدام البيانات التجريبية ونموذج الإجهاد الفعال. يمكن لكل من هذه الطرق حساب احتمالية التميع بسبب مجموعة معينة من ظروف التحميل. تعتمد دقتها على دقة نموذج ضغط المسام المسال الأساسي وعلى مدى دقة تحديد عدم اليقين في معلمات النموذج. تعتمد مجموعة بديلة من الطرق على توصيف مقاومة التميع القائم على الاختبار في الموقع (على سبيل المثال Christian and Swiger، 1975؛ Yegian and Whitman، 1978؛ Veneziano and Liao، 1984؛ Liao et al، 1988). تستخدم هذه الطرق تصنيفات إحصائية مختلفة وتحليلات انحدار لتعيين احتمالات التميع لمجموعات مختلفة من معلمات التحميل والمقاومة. على سبيل المثال، قام Liao et al (1988) بتحليل 278 دراسة حالة لإنتاج التعبير التالي لاحتمالية التميع:

P_L=1/(1+exp[-(β₀+β₁*ln(CSR)+β₂(N₁)₆₀)])

حيث تظهر المعلمات β₀-β₂ في الجدول 4. تظهر منحنيات احتمالية التميع لحالات الرمل النظيف والطمي بيانياً في الشكل (9.44).

المثال الخامس:

استخدم نهج Liao et al (1988) لتقدير احتمالات التميع في الموقع الموصوف في المثال الرابع.

الحل يمكن استخدام بيانات σ’_v0 وτ_cyc من المثال الرابع لحساب نسبة الإجهاد الدوري (العمود 4 في الجدول 5). باستخدام نسبة الإجهاد الدوري هذه وقيم (N₁)₆₀ التي تم تقييمها في الأصل، احتمالات التميع عند كل عمق في ملف تعريف التربة (مع معاملات انحدار الرمال النظيفة) في الجدول. وعلى الرغم من أن نتائج هذا التحليل معبر عنها من حيث احتمال التميع وليس عامل الأمان ضد التميع (كما في المثال الرابع)، فإن كلاهما يشير إلى أنه كان من المتوقع حدوث تميع واسع النطاق في هذا الموقع المعين في زلزال نيجاتا عام 1964. وقد لوحظ بالفعل تميع واسع النطاق في المواقع ذات ظروف التربة المماثلة لتلك في ذلك الزلزال.

الشكل(4)

الجدول(9.3)

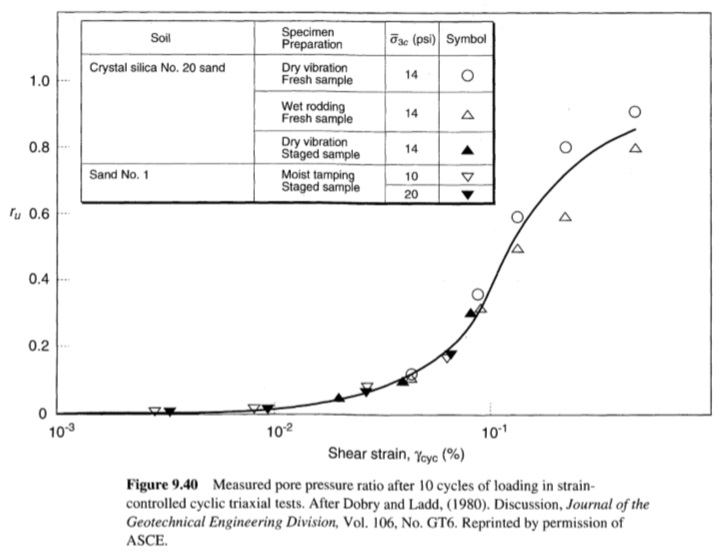
الشكل(9.40)

الشكل(9.41)

الشكل(9-43)

الشكل(9.43)

الجدول(4)

الجدول(5)

الشكل(9.44)

تأثيرات التميع

يمكن لظاهرة التميع أن تؤثر على المباني والجسور وخطوط الأنابيب المدفونة وغيرها من المرافق المشيدة بطرق مختلفة عديدة. كما يمكن أن يؤثر التميع على طبيعة حركات سطح الأرض. يمكن أن ينتج التميع التدفقي انزلاقات تدفقية ضخمة ويساهم في غرق أو إمالة الهياكل الثقيلة، وتعويم الهياكل الخفيفة المدفونة، وفشل الهياكل الاحتجازية. يمكن أن تتسبب الحركة الدورية في انحدار المنحدرات، وهبوط المباني، والانتشار الجانبي، وفشل الجدار الاحتجازي. يمكن أن تتطور تذبذبات أرضية كبيرة، وهبوط سطح الأرض، وغليان الرمال، وفشل الاستقرار بعد الزلزال في المواقع ذات الأرض المستوية. يمكن تقدير تأثيرات التميع بشكل أفضل من خلال دراسة الحالات التاريخية الموثقة جيدًا. بالإضافة إلى المجلات المنشورة بانتظام والتي تتعامل مع هندسة الزلازل الجيوتقنية، يمكن العثور على مجموعة ممتازة من الحالات التاريخية في Hamada and O’Rourke (1992).

تغير حركة الأرض:

إن تأثير معامل القص وخصائص التخميد للتربة على استجابة الأرض أمر معروف. وقد أظهرت العديد من الأمثلة على تأثيرات هذه الخصائص أن رواسب التربة اللينة تستجيب بشكل مختلف عن رواسب التربة الصلبة لنفس الحركة. ويؤدي تطور ضغوط المسام الزائدة الإيجابية إلى انخفاض صلابة التربة أثناء الزلزال. وقد تصبح رواسب التربة القابلة للتحويل إلى سائل والتي تكون صلبة نسبيًا في بداية الزلزال أكثر ليونة بكثير بحلول نهاية الحركة. ونتيجة لذلك، قد يتغير محتوى سعة وتردد حركة السطح بشكل كبير طوال الزلزال. وفي الحالة الأكثر تطرفًا، يمكن أن يؤدي تطور ضغوط المسام العالية جدًا إلى انخفاض صلابة (وقوة) حتى الطبقة الرقيقة إلى الحد الذي لا يمكن معه نقل المكونات عالية التردد لحركة الأساس الصخري إلى سطح الأرض. ويظهر مثال على هذا التأثير في الشكل (9.45). ليس من الصعب تحديد النقطة التي حدث عندها انخفاض صلابة التربة الأساسية بسبب التميع – فقد تغيرت سعة التسارع ومحتوى التردد بشكل كبير بعد حوالي 7 ثوانٍ من الحركة. إن حقيقة أن سعة تسارع السطح تنخفض عندما تصبح ضغوط المسام كبيرة لا تعني بالضرورة أن احتمال الضرر ينخفض ​​​​لأن سعة التسارع المنخفضة عند الترددات المنخفضة يمكن أن تنتج إزاحات كبيرة. قد تكون هذه الإزاحات مثيرة للقلق بشكل خاص للهياكل المدفونة والمرافق والهياكل المدعومة على أسس أكوام تمتد عبر التربة المسالة (الشكل 9.46). يمكن أن يؤدي حدوث التميع في العمق تحت سطح الأرض المستوية إلى فصل التربة المسالة عن التربة السطحية وإنتاج تذبذبات أرضية كبيرة ومؤقتة. غالبًا ما تنكسر التربة السطحية إلى كتل (الشكل 9.47) مفصولة بشقوق يمكن أن تفتح وتغلق أثناء الزلزال. تم رصد موجات أرضية بسعة تصل إلى عدة أقدام أثناء تذبذب الأرض، ولكن النزوح الدائم عادة ما يكون صغيرا.

وقد عزا Youd (1993) إلى تذبذبات الأرض معظم الحركات الأرضية الفوضوية التي تسببت في تشقق وانحناء الأرصفة في منطقة مارينا في سان فرانسيسكو أثناء زلزال لوما بريتا عام 1989. ومن الصعب للغاية التنبؤ بسعة تذبذبات الأرض في موقع معين؛ فحتى تحليلات الاستجابة الأرضية غير الخطية التفصيلية لا يمكنها أن تقدم سوى تقديرات أولية.

تطور الغليان الرملي:

غالبًا ما يصاحب التميع تطور الغليان الرملي. وأثناء وبعد اهتزاز الزلزال، تتبدد الضغوط الزائدة في المسام الناجمة عن الزلازل بشكل أساسي عن طريق التدفق الصاعد لمياه المسام. وينتج عن هذا التدفق قوى مؤثرة لأعلى على جزيئات التربة [يمكن لهذه القوى أن تؤدي إلى إرخاء الجزء العلوي من الرواسب وتركها في حالة قابلة للتميع في زلزال مستقبلي (Youd، 1984 a)[. إذا وصل التدرج الهيدروليكي الذي يحرك التدفق إلى قيمة حرجة، فإن الإجهاد الفعال الرأسي سينخفض ​​إلى الصفر وستكون التربة في حالة سريعة. في مثل هذه الحالات، قد تكون سرعات المياه كافية لحمل جزيئات التربة إلى السطح. في الحقل، نادرًا ما تكون ظروف التربة موحدة، لذا فإن مياه المسام الهاربة تميل إلى التدفق بسرعة عالية عبر الشقوق أو القنوات الموضعية. يمكن حمل جزيئات الرمل عبر هذه القنوات وقذفها على سطح الأرض لتكوين غليان الرمل. يعد تطور غليان الرمل عملية معقدة وعشوائية إلى حد ما؛ فهو يعتمد على حجم ضغط المسام الزائد؛ وسمك وكثافة وعمق منطقة ضغط المسام الزائد؛ وسمك ونفاذية وسلامة أي طبقات تربة تغطي منطقة ضغط المسام الزائد العالي. هناك فخاخ للاعتماد على وجود غليان الرمل للحصول على دليل على الظواهر المرتبطة بالتميع؛ قد لا ينتج التميع على أعماق كبيرة أو في طبقات رقيقة غليانًا رمليًا، ولكن قد ينتج عنه ضغوط مسام زائدة أقل في طبقات سميكة على أعماق ضحلة. كما أن النفاذية المنخفضة للرمال الطينية قد تمنع مياه المسام من التدفق بسرعة كافية لإنتاج غليان الرمل، حتى لو تطورت ضغوط مسام زائدة عالية. فحص Ishihara (1985) ظروف التربة المرتبطة بتقارير الأضرار المختلفة المتعلقة بالتميع من زلزال نيهونكاي-تشوبو عام 1983 (M = 7.7) وزلزال تانغشان عام 1976 (Gao et al. 1983) وأنتج تقديرات لسمك الطبقة العلوية المطلوبة لمنع الأضرار المرتبطة بالتميع على مستوى الأرض (الشكل 9.48). تم التحقق من صحة هذه التقديرات مقابل قاعدة بيانات أكبر بكثير للمواقع غير المعرضة لتذبذب الأرض أو الانتشار الجانبي، لكنها غير كافية للتنبؤ بالأضرار في مواقع أخرى (Youd and Garris، 1995). غليان الرمل ليس له أهمية هندسية في حد ذاته، لكنه مؤشرات مفيدة لتوليد ضغط مسام زائد مرتفع. وقد أظهرت اختبارات طاولة الاهتزاز (Liu and Qiao, 1984) وأجهزة الطرد المركزي (Fiegel and Kutter, 1992) أن مياه المسام التي تتسرب من فراغات الطبقات الرخوة يمكن أن تتراكم تحت الطبقات الأقل نفاذية وتشكل طبقات مائية (الشكل 9.49). ويمكن أن تتطور غليان الرمل عندما تخترق طبقات المياه سطح الأرض. ومن المرجح أيضًا أن يصاحب تكوين طبقات المياه إعادة توزيع معينة؛ وتحديدًا، قد تتحرر الرمال الموجودة أسفل طبقة المياه مباشرةً بسبب تدفق المياه لأعلى نحو الطبقة. وإذا نشأت مثل هذه الظروف أسفل سطح أرضي مائل، فإن وجود طبقة المياه وانخفاض قوة الحالة المستقرة للرمل المتحرر مباشرةً أسفلها يمكن أن يساهم في تشوهات تدفق كبيرة. تنشأ ترسبات سطح الأرض من الإجهاد الحجمي الذي يتطور مع تبدد ضغوط المسام المستحثة زلزاليًا. ويتم توضيح هذه الظاهرة لتوضيح التربة في الشكل (9.50). في البداية، يكون العنصر في حالة توازن مستنزف (صفر ضغط زائد للمسام) عند النقطة A. يتسبب اهتزاز الزلزال في تراكم ضغط المسام الزائد في ظل ظروف غير مستنزفة، وبالتالي تقليل الإجهاد الفعال إلى ما هو موضح عند النقطة B. ينتج ضغط المسام الزائد تدرجًا هيدروليكيًا يدفع مياه المسام إلى خارج الفراغات. يقلل تدفق الماء من التدرج الهيدروليكي حتى يتبدد ضغط المسام الزائد تمامًا (النقطة C). مع تدفق الماء من الفراغات، ينخفض ​​حجم العنصر. وكما يوضح الشكل (9.50) بوضوح، فإن حجم التغير في الحجم يزداد مع حجم ضغط المسام الزائد الناجم عن الزلازل. حتى ضغوط المسام الزائدة الصغيرة التي قد لا تكون كافية لإنتاج تميع التدفق أو الحركة الدورية، يمكن أن تنتج بعض الترسيبات بعد الزلزال.

الترسيب:

إن ميل الرمال إلى التكاثف عند تعرضها لهزات زلزالية أمر موثق جيدًا. ويتجلى التكاثف تحت السطح على سطح الأرض في شكل ترسيب. ويتسبب الترسيب الناجم عن الزلازل في كثير من الأحيان في إحداث ضرر للهياكل المدعومة على أسس ضحلة، وإلحاق الضرر بالمرافق التي تخدم الهياكل المدعومة بالأكوام، وإلحاق الضرر بخطوط الحياة التي تُدفن عادةً على أعماق ضحلة. وتتكاثف الرمال الجافة بسرعة كبيرة؛ وعادة ما يكتمل ترسيب رواسب الرمال الجافة بحلول نهاية الزلزال. ويتطلب ترسيب رواسب الرمال المشبعة وقتًا أطول، ولا يمكن أن يحدث الترسيب إلا عندما تتبدد ضغوط المسام الناجمة عن الزلزال. ويعتمد الوقت المطلوب لحدوث هذا الترسيب على نفاذية التربة وقابليتها للضغط، وعلى طول مسار الصرف، يمكن أن يتراوح من بضع دقائق إلى حوالي يوم واحد. إن تقدير ترسيبات الرمال الناجمة عن الزلزال أمر صعب. والأخطاء التي تتراوح بين 25 إلى 50% شائعة في تنبؤات الترسيب الساكن؛ إن الدقة المتوقعة في حالة التحميل الزلزالي الأكثر تعقيداً أقل من ذلك بكثير. ومع ذلك، فقد ثبت أن الإجراءات التالية تنتج نتائج تتفق بشكل معقول مع العديد من حالات السلوك الميداني الملحوظ.

ترسيب الرمال الجافة:

تعتمد كثافة الرمال الجافة المعرضة للتحميل الزلزالي على كثافة الرمال، وسعة إجهاد القص الدوري المستحث في الرمال، وعدد دورات إجهاد القص المطبقة أثناء الزلزال (Silver and Seed, 1971). يمكن تقدير الترسيبات باستخدام تحليلات استجابة الأرض التفصيلية مع التصحيحات لتأثيرات الاهتزاز متعدد الاتجاهات (Seed and Silver, 1972؛ Pyke et al., 1975)، أو من خلال إجراءات مبسطة (Tokimatsu and Seed, 1987). في الإجراء المبسّط، يتم تقدير إجهاد القص الدوري الفعال، ϒ_cyc، من خلال إجراء مماثل لذلك المقترح لنهج الإجهاد الدوري لبدء التميع.

نظرًا لأن معامل القص يختلف مع ϒ_cyc، فقد تكون هناك حاجة إلى عدة تكرارات لحساب قيمة ϒ_cyc متوافقة مع معامل القص. يمكن استخدام الشكل (9.51) لتقدير ϒ_cyc عندما تكون G_max معروفة. يمكن بعد ذلك استخدام إجهاد القص الدوري الفعال، جنبًا إلى جنب مع الكثافة النسبية أو مقاومة SPT للرمل، لتقدير الإجهاد الحجمي بسبب الضغط ε_c من الشكل 9.52. تستند البيانات من الشكل (9.52) إلى 15 دورة من الإجهاد، والتي تتوافق مع زلزال بقوة M = 7.5. بالنسبة للزلازل ذات الأحجام الأخرى، يمكن تحديد الإجهاد الحجمي الناتج عن الضغط من نسبة الإجهاد الحجمي الموضحة في الجدول 9.4. باتباع النتائج التجريبية لـ (Pyke et al., 1975) يتم حساب تأثير الاهتزاز متعدد الاتجاهات عن طريق مضاعفة ε_c,M اقترح Pyke et al., 1975)) أيضًا أن المكون الرأسي لحركة الأرض يمكن أن يتسبب في زيادة إضافية بنسبة 50% في الاستقرار (فوق ذلك الناتج عن المكونات الأفقية)؛ لا يتم حساب تأثير الحركة الرأسية صراحةً في الإجراء المبسط لـ Tokimatsu and Seed (1987). نظرًا لأن سعات الصلابة والكثافة وإجهاد القص تختلف عادةً مع العمق، فإن رواسب التربة المعينة تنقسم عادةً إلى طبقات فرعية، مع حساب استقرار كل طبقة فرعية ومجموعها للحصول على إجمالي استقرار سطح الأرض.

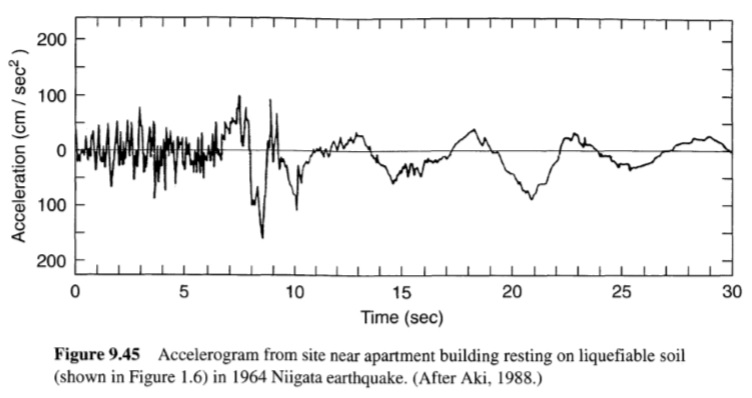
الشكل(9.45)

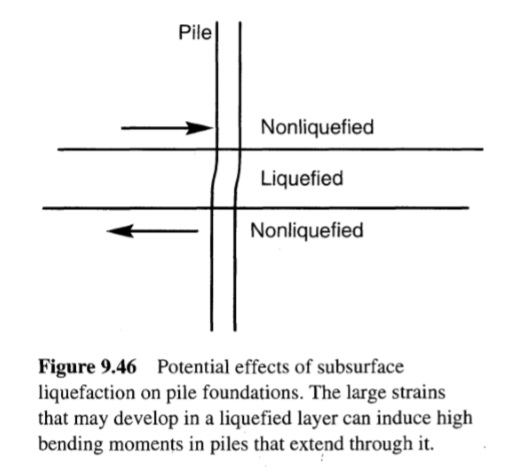
الشكل(9.46)

الشكل(9.47)

الشكل(9.48)

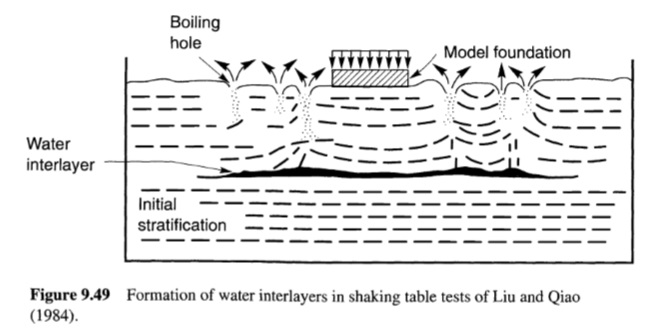
الشكل(9.49)

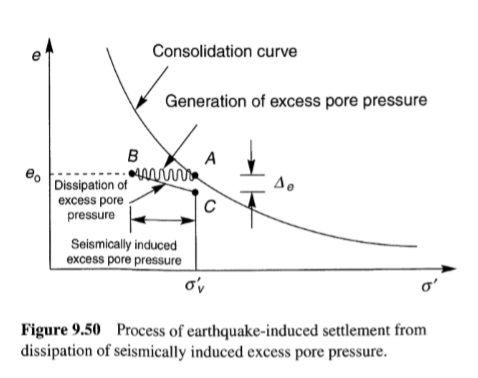
الشكل(9.50)

الشكل(9.51)

الشكل(9.52)

الجدول(9.4)

المثال السادس:

تقدير ترسب رواسب رملية سائبة سمكها 50 قدمًا (Dr=45%) بمقاومة SPT مصححة متوسطة تبلغ 9 لزلزال بقوة 6.6 درجة بواسطة (Seed and Silver, 1972) و(Tokimatsu and Seed, 1987).

الحل يمكن تقسيم الرواسب إلى سلسلة من الطبقات؛ تُستخدم ست طبقات في هذا المثال كما هو موضح في الجدول(5). بناءً على قيم (N₁)₆₀ المعطاة، يمكن تقدير G_max باستخدام العلاقة بين (Ohto and Goto 1976) الواردة في الجدول (العمود 5). يسمح هذا بتقدير ϒ_cyc (العمود 6) باستخدام الشكل 9.51. يمكن بعد ذلك الحصول على الانفعال الحجمي الناتج (لزلزال بقوة 7.5 درجة) من الشكل 9.52 (والعمود 7). وباستخدام الجدول، فإن الإجهاد الحجمي في زلزال بقوة 6.6 درجة على مقياس ريختر يجب أن يكون حوالي 80% من الإجهاد الحجمي في زلزال بقوة 7.5 درجة على مقياس ريختر (العمود 8). وبعد مراعاة الاهتزازات متعددة الاتجاهات، يتم مضاعفة الإجهاد الحجمي (العمود 9). وأخيرًا، يمكن تقدير هبوط كل طبقة على أنه حاصل ضرب الإجهاد الحجمي في سمك الطبقة (العمود 10).

وتتوافق هذه الهبوطات مع تلك التي لوحظت في موقع بهذه الظروف في زلزال سان فرناندو عام 1971 (Tokimatsu and Seed، 1987). ويهدف عدد الأرقام المهمة في هذا المثال إلى تسهيل فهم الحسابات، وليس الإيحاء بأن النتائج دقيقة إلى 0.01 بوصة.

ترسيب الرمال المشبعة:

يتأثر تكثيف الرمال المشبعة بعد الزلزال بكثافة الرمال، وأقصى إجهاد قص يحدث في الرمال، وكمية الضغط الزائد في المسام الناتج عن الزلزال. وقد أظهرت التجارب المعملية أن الإجهاد الحجمي بعد التميع الأولي يختلف باختلاف الكثافة النسبية وأقصى إجهاد قص. استخدم Tokimatsu and Seed (1987) الارتباط بين (N₁)₆₀ والكثافة النسبية وتقديرًا لإمكانية إجهاد القص للتربة المسالة من (N₁)₆₀ ونسبة الإجهاد الدوري (Seed et al, 1984) لإنتاج مخطط (الشكل 9.53) يسمح بتقدير الإجهاد الحجمي بعد التميع في زلزال بقوة M = 7.5 مباشرة من نسبة الإجهاد الدوري ومقاومة SPT. بالنسبة للزلازل ذات الأحجام الأخرى، يمكن تحديد نسبة الإجهاد الدوري المكافئة، CSR_M، من الجدول 9.2. لاحظ أن الإجهاد الحجمي بعد التميع يمكن أن يصل إلى 2 إلى 3% للرمال السائبة إلى متوسطة الكثافة وأعلى للرمال السائبة جدًا؛ طبقة من الرمال السائبة جدًا بسمك   16قدمًا أنتجت ترسبات تتراوح من 50 إلى 70 سم (20 إلى 28 بوصة) في هاشينوهي، اليابان بعد زلزال توكاتشيوكي (M = 7.9) في عام 1968 (Ohsaki, 1970)؛ لوحظت ترسبات تتراوح من 50 إلى 100 سم (20 إلى 39 بوصة) في جزيرة بورت وجزيرة روكو في كوبي، اليابان بعد زلزال هيوغو كين نانبو عام 1995. إذا تم إنتاج غليان الرمل، فمن المرجح أن تكون الترسبات بعد الزلزال غير منتظمة. يمكن أن تكون الحركة التفاضلية الناتجة ضارة بالهياكل أو الأرصفة أو خطوط الأنابيب على سطح الأرض أو بالقرب منه.

الجدول(5)

الشكل(9.53)

المثال السابع:

لوحظت ترسبات كبيرة في منطقة مارينا في سان فرانسيسكو في أعقاب زلزال لوما بريتا عام 1989. وقد تبين أن جزءًا كبيرًا من هذه الترسبات قد نتج عن تكثيف الحشوات الهيدروليكية التي وُضعت لاستعادة المنطقة من خليج سان فرانسيسكو في تسعينيات القرن التاسع عشر. تظهر الظروف تحت السطح في أحد مواقع منطقة مارينا في الشكل 7 (O’Rourke et al., 1991). قم بتقدير الترسبات التي كان من المتوقع حدوثها في هذا الموقع في زلزال لوما بريتا. تم قياس تسارع الذروة بمقدار 0.20g في محيط منطقة مارينا. الحل يُظهر ملف تعريف تحت السطح مقاومات SPT مقاسة (غير مصححة). وبافتراض أن مقاومات SPT تم قياسها باستخدام الإجراءات القياسية (E_m= 0.60E_ff)، يمكن حساب مقاومات SPT (العمود 4 الجدول 6). يمكن استخدام الإجراء المبسّط Seed and Idris (1971) لتقدير نسبة الإجهاد الدوري (العمود 5 الجدول 6).

يمكن بعد ذلك تقدير الإجهاد الحجمي باستخدام الشكل 9.53. ثم يتم حساب استقرار كل طبقة على أنه حاصل ضرب الإجهاد الحجمي وسمك الطبقة. كانت الاستقرارات الفعلية في محيط هذا الموقع في حدود 12 إلى 15 سم. نتجت بعض الاستقرارات الفعلية عن تكثيف التربة الجافة فوق منسوب المياه؛ ولم يتم أخذ هذا الاستقرار في الاعتبار في هذا المثال.

في نهج بديل، يمكن استخدام عامل الأمان ضد التميع أو أقصى إجهاد قص دوري، والكثافة النسبية، ومقاومة SPT، أو مقاومة CPT، لتقدير الإجهاد الحجمي بعد التميع (الشكل 9.54). يؤدي دمج هذه الضغوط الحجمية على سمك الطبقة المسالة إلى حدوث استقرار سطح الأرض.

الشكل(7)

الجدول(6)

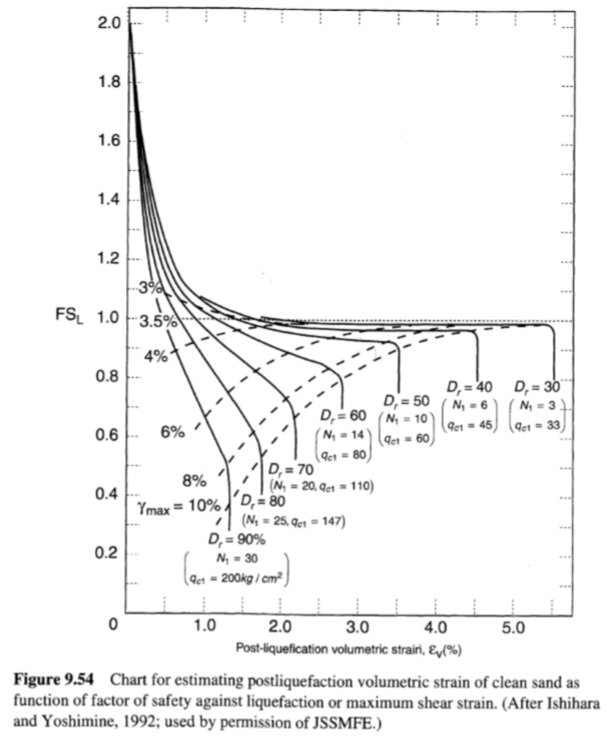
الشكل(9.54)

المثال الثامن: كرر المثال السابع باستخدام طريقة إيشيهارا-يوشيمين. الحل تتطلب طريقة إيشيهارا-يوشيمين تقييم عامل الأمان ضد التميع. باستخدام قيم (N₁)₆₀ من المثال السابع والشكل 9.31، يمكن تحديد نسبة الإجهاد الحرج (المصححة بالحجم) المطلوبة لبدء التميع (العمود 4 الجدول 7). باستخدام قيم CSR من المثال السابع، يمكن حساب عامل الأمان ضد التميع لكل طبقة. بعد ذلك يجب تحويل قيم (N1)60 إلى قيم N1 [تذكر أن إجراءات SPT اليابانية تنقل عادةً 20% طاقة أكثر إلى جهاز أخذ العينات SPT؛ وبالتالي N₁ = 0.833*(N₁)₆₀. باستخدام القيم الناتجة لـ FS_L، يمكن استخدام الشكل 9.54 لتقدير الإجهاد الحجمي في كل طبقة (العمود 8 الجدول 7). مرة أخرى، يتم تحديد استقرار كل طبقة (العمود 9 الجدول 7) من خلال حاصل ضرب الإجهاد الحجمي وسمك الطبقة. يتم حساب الاستقرار الكلي على أنه 17.7 سم بواسطة إجراء إيشيهارا-يوشيمين. وبالتالي فإن إجراءي توكيماتسو-سيد وإيشيهارا-يوشيمين قدموا تقديرات جيدة للاستقرار الملحوظ بعد الزلزال في هذا الموقع. أوضح Ishihara (1993) استخدام إجراء إيشيهارا-يوشيمين لموقع قريب (بسمك أصغر من الحشو الهيدروليكي) باستخدام بيانات CPT؛ تم التنبؤ باستقرار يبلغ 7.3 سم.

الجدول(7)

في كثير من الحالات، تنتج حركة الأرض القوية ضغوطًا زائدة في المسام غير كافية لإنتاج التميع الأولي. ومع ذلك، سوف تتبدد ضغوط المسام هذه، وقد تنتج بعض التغيير في الحجم. قام Tokimatsu and Seed (1987) بدمج العلاقة بين نسبة الإجهاد الطبيعية، CSR/CSR_L، ونسبة ضغط المسام (Tokimatsu and Yoshimi، 1983) والعلاقة بين نسبة ضغط المسام والإجهاد الحجمي (Lee and Albaisa، 1974) لتطوير العلاقة الموضحة في الشكل 9.55. يمكن استخدام الشكل 9.55 لتقدير الإجهاد الحجمي للحالات التي تكون فيها نسبة ضغط المسام القصوى أقل من 100%. لاحظ أن التغيرات في الحجم بعد الزلزال صغيرة جدًا ما لم تكن نسبة CSR أكبر من 70 إلى 80٪ من تلك المطلوبة للتسبب في التميع الأولي (r_u=100%). يعتمد معدل تطور الترسيب على خصائص إعادة التماسك للتربة المسالة. تبدأ إعادة التماسك عمومًا في قاع التربة المسالة (Florin and Ivanov, 1961; Heidari and James, 1982) وتستمر إلى الأعلى. نظرًا لأن الضغوط الفعالة يمكن أن تختلف على مدى عدة أوامر من حيث الحجم أثناء إعادة التوحيد، فإن نماذج التوحيد غير الخطية مطلوبة للتنبؤ بمعدلات التسوية (Whitman et al., 1982: Scott, 1986).

عدم الاستقرار

إن عدم الاستقرار الناجم عن التميع يعد من أكثر المخاطر الزلزالية ضرراً. وقد لوحظت آثاره في هيئة انزلاقات تدفقية، وانتشارات جانبية، وانهيارات جدران الاحتفاظ، وانهيارات الأساسات في عدد لا يحصى من الزلازل في جميع أنحاء العالم. ويمكن أن تنتج حالات عدم الاستقرار عن ظواهر التميع المختلفة، وليس من الواضح دائماً أي منها مسؤول عن فشل معين. ومع ذلك، تتأثر جميعها بقوة القص للتربة المسالة.

الشكل(9.55)

قوة القص للتربة المسالة:

يحدث عدم الاستقرار عندما تتجاوز إجهادات القص المطلوبة للحفاظ على توازن رواسب التربة قوة القص لتلك الرواسب. ثم تتشوه التربة حتى تصل إلى تكوين لا تتجاوز فيه إجهادات القص قوة القص. ويتأثر مقدار التشوه المطلوب للوصول إلى تكوين مستقر بشدة بالفرق بين إجهادات القص المطلوبة للتوازن وقوة القص للتربة المسالة. إذا كانت قوة القص للتربة المسالة أقل قليلاً فقط من إجهاد القص المطلوب للتوازن، فمن المرجح أن تكون التشوهات الدائمة صغيرة. إذا كان الفرق بين قوة القص وإجهاد القص كبيرًا، فقد تتطور تشوهات كبيرة جدًا. يتطلب التقييم الدقيق لتأثيرات عدم الاستقرار الناجم عن التميع تقديرًا دقيقًا لقوة القص للتربة المسالة. تم تطوير ثلاثة مناهج مختلفة لتقدير قوة القص للتربة المسالة. يعتمد أحدها على برنامج أخذ العينات غير المضطربة والاختبارات المعملية. يعتمد الآخر على معاملات الاختبار في الموقع وتفسير حالات التميع المعروفة. يعامل الثالث قوة القص للتربة المسالة كقوة طبيعية. نهج الاختبار المعملي: قوة الحالة المستقرة. تحكم قوة الحالة المستقرة سلوك التربة المسالة. من حيث المفهوم، إنها دالة لكثافة التربة فقط، على الرغم من أن بعض الدراسات التجريبية تشير إلى أنها قد تتأثر بمسار الإجهاد وعوامل أخرى. بالنسبة للعديد من الترب، تكون قوة الحالة المستقرة حساسة للغاية للكثافة (أي أن التغييرات الصغيرة في الكثافة يمكن أن تؤدي إلى تغييرات كبيرة في قوة الحالة المستقرة). إذا كان من الممكن أخذ عينات من تربة عديمة التماسك “بشكل مثالي” (أي بدون أي اضطراب على الإطلاق)، فيمكن قياس قوة الحالة المستقرة، S_su، لعينة معينة في اختبار ثلاثي المحاور واحد عن طريق توحيد العينة لظروف الإجهاد في الموقع ثم قصها في ظل ظروف غير مستنزفة باتباع مسار الإجهاد الأكثر ملاءمة. لسوء الحظ، تتسبب أعمال أخذ العينات والنقل والمناولة والتوحيد في حدوث تغييرات في كثافة العينة المعملية بحلول وقت اختبارها. ونظرًا لحساسية S_su، للكثافة، فيجب تصحيح قوة الحالة المستقرة لعينة معملية لتتوافق مع نسبة الفراغ في الموقع Poulos et al (1985) اقترح الإجراء التالي المكون من أربع خطوات لقياس قوة الحالة المستقرة في الموقع. يتم توضيح الإجراء بيانياً في الشكل 9.56.

1. تحديد نسبة الفراغات في الموقع من عينة واحدة أو أكثر “غير مضطربة”. هذه هي الخطوة الأكثر أهمية والأكثر صعوبة في الإجراء بأكمله. اقترح بولوس وآخرون (1985) ثلاث إجراءات مرضية لأخذ العينات: (1) أخذ العينات بمكبس ثابت، (2) تجميد الأرض وأخذ العينات، و (3) أخذ العينات في حفر الاختبار. لا يمكن المبالغة في التأكيد على أهمية أخذ العينات بعناية لنجاح هذا الإجراء.
2. تحديد موقع خط الحالة المستقرة باستخدام عينات أعيد تكوينها. نظرًا لأن ميل خط الحالة المستقرة يتأثر بشكل أساسي بشكل الحبوب، فيجب أن يكون لخط الحالة المستقرة من سلسلة من العينات المعاد تكوينها نفس ميل التربة في الموقع. من المقترح إجراء اختبارات على خمس أو ست عينات تم توحيدها إلى حالات أولية أعلى بكثير من مستوى SSL (لضمان السلوك الانكماشي).
3. تحديد قوة الحالة المستقرة لعينة غير مضطربة. يتم إجراء اختبار ثلاثي المحاور متماسك وغير مستنزف على عينة تم الحصول عليها من الخطوة 1 لضمان الوصول إلى الحالة المستقرة عند مستويات إجهاد معقولة، يُقترح التماسك إلى ضغوط احتواء فعّالة مرتفعة (مرة أخرى، لإنتاج سلوك انكماشي).
4. تصحيح قوة الحالة المستقرة المقاسة إلى نسبة الفراغات في الموقع. بافتراض أن SSL للعينة غير المضطربة لها نفس ميل العينات المعاد تكوينها، يمكن إيجاد قوة الحالة المستقرة في الموقع من خلال رسم خط عبر النقطة التي تصف العينة غير المضطربة (من الخطوة 3) موازيًا لـ SSL (من الخطوة 2) والعودة إلى نسبة الفراغات في الموقع (من الخطوة 1). يتم أخذ القوة الناتجة كقوة الحالة المستقرة في الموقع.

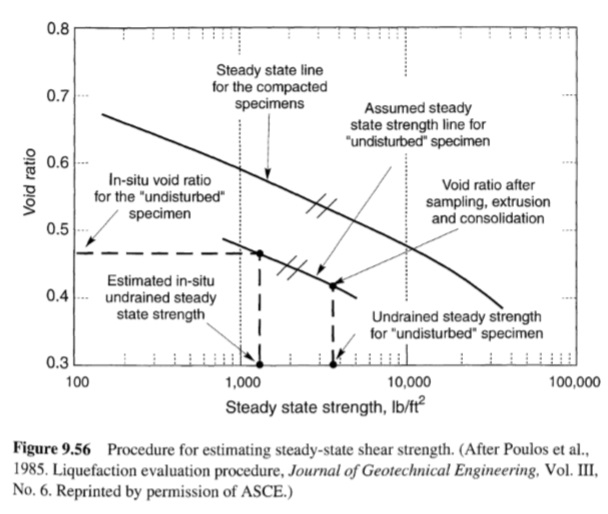
الشكل(9.56)

يمكن بعد ذلك استخدام قوة الحالة الثابتة المصححة في الموقع لتقييم مخاطر التميع المحتملة. وعلى الرغم من أن هذا الإجراء عقلاني، يجب أن يظل المستخدم على دراية بحساسية النتائج لعدم اليقين في معلمات الإدخال، وخاصة نسبة الفراغ في الموقع. قدم Kramer (1989) إجراءً لتقدير عدم اليقين في S_su.

نهج الاختبار في الموقع: القوة المتبقية:

كبديل للإجراءات القائمة على المختبر، طور Seed (1986) ارتباطًا بين مقاومة SPT وقوة القص الظاهرة المحسوبة من شرائح التدفق المرصودة. نظرًا لعدم وجود ضمان بأن جميع شروط الحالة المستقرة للتشوه قد تم الوفاء بها في حالات التاريخ – في الواقع، اقترح Stark and Mesri (1992) أن الصرف الجزئي حدث قبل أن تصل بعض شرائح التدفق إلى حالة الراحة – فإن القوة المحسوبة من الخلف تسمى القوة المتبقية. Seed and Harder (1990) أعادا تحليل العديد من شرائح التدفق وأضافا بيانات جديدة لتطوير علاقة بين القوة المتبقية ومقاومة SPT المكافئة للرمال النظيفة (الشكل 9.57)، يتم الحصول على مقاومة SPT المكافئة للرمال النظيفة من:

(N₁)_60-cs = (N₁)₆₀ + N_corr

حيث يتم الحصول على N_corr، من الجدول 9-5.

إن إجراءات الحساب العكسي المستخدمة للحصول على القوة المتبقية ليست بسيطة – فهي تتضمن العديد من الافتراضات والتقديرات. وبالاقتران مع تباين SPT وصعوبة اختيار قيمة SPT واحدة لتمثيل كل حالة، يجب اعتبار هذه القوى المتبقية تقريبية، كما يشير النطاق العريض في الشكل 9.57. ومع توفر المزيد من البيانات وتحسن إجراءات الحساب العكسي، من المرجح أن تقل هذه الشكوك.

الجدول(9.5)

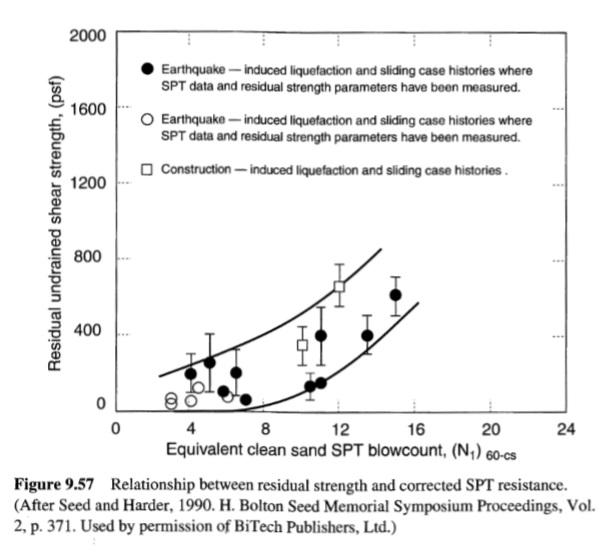
الشكل(9.57)

المثال التاسع:

في زلزال سان فرناندو عام 1971، سالت التربة داخل المنحدر العلوي لسد سان فرناندو السفلي وأنتجت انزلاقًا تدفقيًا كاد يخترق السد. أشارت التحقيقات تحت السطحية إلى أن الرمل الطيني الموضوع هيدروليكيًا في المنحدر العلوي يحتوي على حوالي 25% من الفين وكان متوسطه المقاس (N₁)₆₀ حوالي 11.5. قدر القوة المتبقية للرمل الطيني. الحل بالنسبة للرمل الذي يحتوي على 25% من الفين، فإن N_corr = 2، لذا فإن (N1)_60-cs = 11.5+2= 13.5

بالإشارة إلى الشكل 9.57، يجب أن تكون القوة المتبقية المقدرة بين حوالي 300 و750 رطل/قدم مربع (القيم المعطاة بواسطة المنحنيات العلوية والسفلية). وبالنظر إلى أن البيانات من الحالات التاريخية الفعلية للتميع الناجم عن الزلازل تقع في الجزء السفلي من هذا النطاق، فمن المرجح أن تكون القوة المتبقية في حدود 300 إلى 500 رطل/قدم مربع.

نهج القوة الطبيعية: نسبة القوة المتبقية:

مفهوم القوة الطبيعية مقبول على نطاق واسع في ممارسة الهندسة الجيوتقنية للتربة المتماسكة (Ladd and Foott, 1974). ويمكن أيضًا تطبيق المفهوم العام على القوة المتبقية للتربة المسالة. الميزة المهمة لهذا النهج هي أنه يسمح بتقدير القوة المتبقية من الإجهادات الفعالة الأولية، والتي من الأسهل بكثير تحديدها بدقة من نسب الفراغات الأولية. إذا كان منحنى التماسك وخط الحالة المستقرة للتربة القابلة للتحويل إلى سائل متوازيين، فيجب أن تكون قوة الحالة المستقرة متناسبة مع إجهاد التماسك (أي، S_su/σ’_1c = ثابت). إن تطبيق هذا المفهوم معقد بسبب حقيقة أن التربة الرملية لا تظهر منحنيات تماسك فريدة: وبالتالي فإن النسبة S_su/σ’_1c ليست فريدة لتربة معينة. ومع ذلك، إذا تم تحضير عينات معملية بنفس نسبة الفراغ ونسيج التربة الموجودين في الحقل عند إجهادات فعالة أولية مماثلة، يمكن أن تكون نسب القوة المتبقية المقاسة ممثلة لظروف الحقل (Vasquez-Herrera et al، 1990؛ Baziar et al، 1992؛ Ishihara، 1993). وجد Vasquez-Henera et al., 1990)) أن S_r/σ’_v0 ≈ 0.12 للعينات المعاد تكوينها من الرمل الطيني من سد سان فرناندو السفلي. استخدم Byrne et al., 1993)) العينات التي تم الحصول عليها عن طريق التجميد وأخذ العينات من سد Duncan لقياس S_r/σ’_v0 = 0.21. كما تم استخدام نهج القوة الطبيعية مع قوة البقايا المقاسة في اختبارات القص الريحي الميدانية.

استخدم (Castro and Troncoso, 1989) اختبارات القص الريحي لقياس قيم S_r/σ’_v0  البالغة 0.07، 0.11 و0.08 في الوحل الرخو للغاية (PI  يساوي 20 إلى 22) في ثلاثة سدود مخلفات مختلفة في تشيلي. بالنسبة للطمي الطيني (Finn et al., 1991) في أساس سد Sardis، أشارت اختبارات القص الريحي إلى أن S_r/σ’_v0 ≈ 0.075. تشير البيانات المحدودة المتاحة إلى أن نهج القوة الطبيعية يعد أداة عملية لتقدير القوة المتبقية للتربة المسالة. تشير البيانات بوضوح إلى أن نسب القوة المتبقية يمكن أن تختلف على مدى نطاق كبير وأن تقييمها يتطلب تحقيقًا واختبارًا دقيقًا ومحددًا للموقع. يتطلب نهج القوة الطبيعية الأساسي قياس نسبة القوة المتبقية في الموقع. من المنطقي أن نتوقع أن التربة المختلفة سيكون لها نسب متبقية مختلفة. نسب القوة؛ على سبيل المثال، يجب أن تكون نسبة القوة المتبقية للرمل الزاوي المصنف جيدًا أكبر من نسبة الرمل المستدير المنتظم. وبافتراض أن العوامل التي تؤثر على نسبة القوة المتبقية تؤثر أيضًا على نتائج الاختبار في الموقع، فيجب أن يكون من الممكن ربط نسبة القوة المتبقية بمعلمات الاختبار في الموقع. استخدم Stark and Mesri (1992) قوى متبقية محسوبة عكسيًا ومقاسة في المختبر من حالات ميدانية لربط قيم نسبة القوة المتبقية بمقاومة SPT، أي، حيث يتم حساب

S_r/σ’_v0 = 0.0055*(N₁)_{60 – cs}

باستخدام قيم (N₁)_{60 – cs} الواردة في الجدول 9-5. وعلى الرغم من أن هذا الإجراء له الميزة المهمة المتمثلة في السماح بتقدير نسبة القوة المتبقية من مقاومة SPT، فيجب اعتبار المعادلة تقريبًا متحفظًا بشكل معقول لمجموعة من البيانات التجريبية المتناثرة.

المثال العاشر:

وفقًا لستارك وميسري (1992)، كان ضغط العبء الزائد الفعال في مركز الجزء المسال من المنحدر العلوي لسد سان فرناندو السفلي 3930 رطل/قدم مربع. قدّرت القوة المتبقية لهذه الترب باستخدام نهج ستارك وميسري. الحل وفقًا لنهج ستارك وميسري، فإن الرمل الطيني الذي يحتوي على 25% من المواد الدقيقة سيشير إلى N_corr = 6، لذا فإن (N₁)_60-cs = 11.5 + 6 = 17.5

يمكن تقدير القوة المتبقية على أنها S_r = 0.0055(N₁)_60-cs * σ’_v0= 378 lb/ft²

هذه القيمة متوافقة مع نطاق القيم التي تم الحصول عليها في المثال التاسع.

يعد تقييم القوة المتبقية للرمل المسال أحد أصعب المشكلات في ممارسة هندسة الزلازل الجيوتقنية المعاصرة. تعد مفاهيم الحالة المستقرة مفيدة جدًا لفهم سلوك التربة القابلة للتحويل إلى سائل، ولكن يمكن أن تعتمد قوى الحالة المستقرة على مسار الإجهاد. في الميدان، ينطوي الفشل عمومًا على مسارات إجهاد مختلفة، وبالتالي قوى حالة مستقرة مختلفة، على أجزاء مختلفة من سطح الفشل. علاوة على ذلك، قد يحدث بعض الصرف أثناء الفشل. ونظرًا لهذه العوامل، فليس من المستغرب أن يكون من الصعب تحديد القوى المتبقية. إن نهج الاختبار المعملي عقلاني ويستند إلى اختبارات تكون فيها إجهادات القص معروفة بدقة، ولكن حساسية نتائجه لمعلمات الإدخال غير المؤكدة تؤدي إلى قدر كبير من عدم اليقين في إن تقديرات القوة الثابتة هي طريقة منطقية أيضاً، ولكن تباين ظروف التربة والإجهاد في الحالات التي يستند إليها هذا النهج يُدخل قدراً كبيراً من عدم اليقين في تقديرات القوة المتبقية. وعند مراجعة تطبيق هذه الأساليب على تاريخ حالة سد سان فرناندو السفلي، فضل Marcuson et al (1990) النهج الموجود في الموقع ولكنهم اقترحوا استخدام كليهما حيث تكون المخاطر عالية. يقدم نهج القوة الطبيعية بعض المزايا مقارنة بالطرق الأخرى، ولكن البيانات المتاحة تشير إلى أن نسب القوة المتبقية تختلف بشكل كبير بالنسبة للتربة المختلفة.

فشل التدفق:

يحدث فشل التدفق الناجم عن التميع عندما تكون إجهادات القص المطلوبة للحفاظ على التوازن الثابت أكبر من قوة القص للتربة المسالة. يمكن أن ينشأ هذا الموقف بعدة طرق مختلفة؛ حدد المجلس الوطني للبحوث (1985) أربع آليات مختلفة لفشل التدفق. يعد تقدير التشوهات الناتجة عن فشل التدفق الناجم عن التميع أمرًا صعبًا للغاية.

فشل التميع التدفقي:

يمثل التميع التدفقي آلية فشل تدفق مهمة. يحدث التميع التدفقي في ظل ظروف غير مصفاة تمامًا – لا يوجد إعادة توزيع لمياه المسام (أو تغيير في نسبة الفراغ). يبدأ التميع التدفقي عندما يتم توليد ضغط مسام كافٍ لتحريك مسار الإجهاد الفعال لعنصر من عناصر التربة من موضعه الأولي إلى سطح التميع التدفقي. عندما يحدث ذلك، يصبح العنصر غير مستقر ويبدأ فشل التميع التدفقي في ذلك العنصر من التربة. بعبارة أخرى، يحدث فشل التميع التدفقي في المواقع التي يبدأ فيها التميع عن طريق اهتزاز الزلزال. يمكن استخدام هذه الخصائص للتمييز بين فشل التميع التدفقي وأنواع أخرى من فشل التدفق. غالبًا ما يحدث فشل التميع التدفقي بسرعة كبيرة وينتج حركات تربة كبيرة (الشكل 9.58) يمكن أن بتطور فشل التميع التدفقي تدريجيًا (أي بدء التدفق) قد ينتشر التميع في حجم صغير من التربة لينتج فشل تدفق كبير). عندما يبدأ التميع التدفقي في موقع معين، تنخفض مقاومة القص إلى قوة الحالة المستقرة. يجب بعد ذلك نقل إجهادات القص الثابتة التي قاومت في ذلك الموقع إلى التربة المحيطة. حيث قد تبدأ المزيد من تميع التدفق. مع استمرار إعادة توزيع الإجهادات، تنمو منطقة التميع. في النهاية، قد يتطور انزلاق تدفق هائل.

فشل تدفق التخفيف المحلي:

نظرًا لأن قوة الحالة المستقرة حساسة للغاية لكثافة العديد من الترب. يمكن لكمية صغيرة من التخفيف أن تقلل من قوة الحالة المستقرة بشكل كبير. في بعض الحالات، قد يقلل التخفيف من قوة الحالة المستقرة إلى قيمة أصغر من إجهاد القص المطلوب للتوازن. وبالتالي ينتج فشل التدفق. إذا كانت طبقة الرمل مغطاة بمادة أقل نفاذية لا تسمح بالتصريف أثناء الزلزال نفسه، فإن الحجم الإجمالي للرمل سيظل ثابتًا. ولكن إذا تم الوصول إلى حالة التميع الأولي (الإجهاد الفعال الصفري)، فقد تعيد جزيئات الرمل ترتيب نفسها تحت تأثير الجاذبية بحيث يصبح الجزء السفلي من الطبقة أكثر كثافة والجزء العلوي أكثر ارتخاءً. وإذا ارتخى الجزء العلوي بدرجة كافية لتقليل قوة الحالة المستقرة إلى قيمة أصغر من إجهاد القص الساكن، فقد يحدث فشل محلي في تدفق الارتخاء، كما هو موضح في الشكل 9.59. وفي الحالات القصوى، قد تتكون طبقة مائية بينية تحت المادة الأقل نفاذية. ونظرًا لأن قوة القص للطبقة المائية بينية تكون صفرية، فقد يحدث فشل في التدفق بسهولة.

فشل تدفق الارتخاء العالمي:

ستؤدي ضغوط المسام الزائدة العالية المتولدة في العمق إلى تدفق مياه المسام نحو حدود الصرف أثناء وبعد الزلزال. وكما هو موضح في الشكل 9.60 a، فإن معظم التدفق يتجه عادةً نحو سطح الأرض. وقد ترتخي التربة الضحلة بسبب هذا التدفق إلى الحد الذي تنخفض فيه قوتها في الحالة المستقرة إلى ما دون إجهاد القص المطلوب للحفاظ على التوازن. وعلى النقيض من حالة التراخي المحلي، لا يتم تعويض هذا التراخي عن طريق التكثيف في موقع مختلف. يتم توضيح العملية تخطيطيًا في الشكل 9.60 b. نظرًا لأن قوة الحالة المستقرة لا تقل حتى يتدفق الماء إلى التربة الضحلة، فقد لا يحدث الفشل حتى بعد الزلزال. قد يساهم تشقق التربة السطحية أيضًا في الفشل.

فشل تدفق الواجهة:

يمكن أن تحدث حالات الفشل من نوع التدفق أيضًا عندما تصبح قوة القص للواجهة بين التربة القابلة للتحويل إلى سائل والهيكل أصغر من إجهاد القص المطلوب للتوازن. يعد الفشل الغاطس لأكوام الاحتكاك (DeAlba, 1983) مثالاً على فشل تدفق الواجهة. إذا كانت الواجهة ناعمة، كما هو الحال مع أكوام الفولاذ أو الخرسانة الجاهزة، فإن فشل تدفق الواجهة لا يتطلب تغييرًا في حجم التربة وبالتالي يمكن أن يحدث في الرمال الانكماشية أو المتوسعة.

فشل التشوهات:

لا تتضمن جميع حالات الفشل المرتبطة بالتميع تدفقات ونزوحات كبيرة. يمكن أن تنتج الحركة الدورية تشوهات صغيرة ومتزايدة ودائمة قد تكون كافية بحلول نهاية الزلزال لإحداث أضرار واسعة النطاق. الانتشار الجانبي هو مثال على فشل التشوه. كما هو موضح في الشكل 9.61، يتسبب الانتشار الجانبي في تكسر الطبقات السطحية إلى كتل تتحرك تدريجيًا إلى أسفل المنحدر أو نحو وجه حر أثناء اهتزاز الزلزال. قد يظهر على سطح الأرض شقوق ومنحدرات عند رأس الانتشار الجانبي، ومناطق قص على طول هوامشها الجانبية، وتربة مضغوطة أو ملتوية. تتحرك الكتل السطحية عادة بشكل غير منتظم في الاتجاهين الأفقي والرأسي؛ قد تنفصل المباني وخطوط الأنابيب الممتدة عبر أو من خلال رأس الانتشار الجانبي، وقد تنقطع خطوط الأنابيب التي تعبر الهوامش الجانبية، وقد تنثني الجسور أو خطوط الأنابيب. تتراوح الإزاحات الجانبية عادة من بضعة سنتيمترات إلى متر أو مترين، ولكنها قد تكون أكبر إذا كان الاهتزاز قويًا بشكل خاص أو طويل الأمد.

الشكل(9.58)

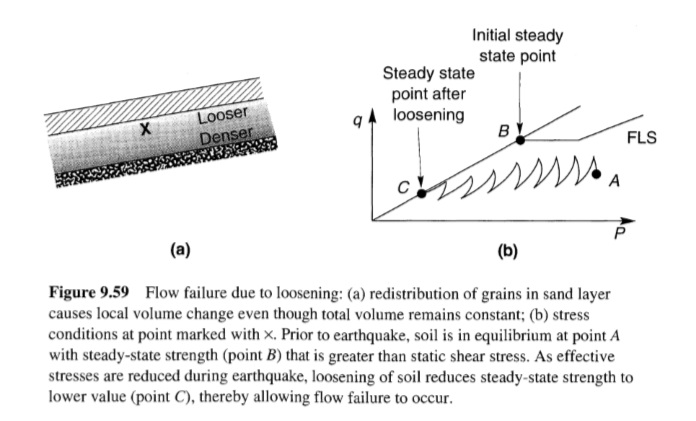
الشكل(9.59)

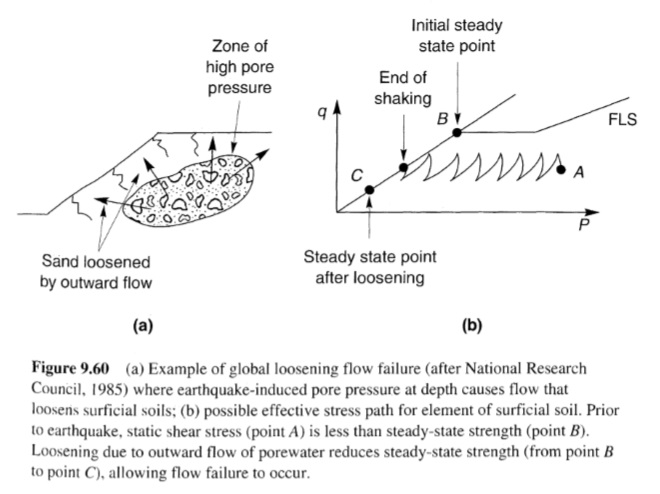
الشكل(9.60)

الشكل(9.61)

الملخص:

1. استُخدم مصطلح التميع لوصف عدد من الظواهر ذات الصلة ولكن المختلفة التي لوحظت في التربة المشبعة الرخوة. ولأغراض هندسية، يمكن تقسيم هذه الظواهر إلى ثلاث مجموعات رئيسية: التميع التدفقي، والحركة الدورية، والتميع على مستوى الأرض.
2. يمكن أن يحدث التميع التدفقي عندما يكون إجهاد القص الساكن في رواسب التربة القابلة للتميع أكبر من قوة الحالة المستقرة للتربة. ويمكن أن ينتج عنه فشل مدمر في انزلاق التدفق أثناء أو بعد اهتزاز الزلزال. يمكن أن يحدث التميع التدفقي فقط في التربة الرخوة.
3. يمكن أن يحدث التنقل الدوري عندما يكون إجهاد القص الساكن أقل من قوة الحالة المستقرة ويكون إجهاد القص الدوري كبيرًا بما يكفي لتجاوز قوة الحالة المستقرة مؤقتًا. تتطور التشوهات الناتجة عن الحركة الدورية تدريجيًا ولكنها يمكن أن تصبح كبيرة بحلول نهاية زلزال قوي أو طويل الأمد. يمكن أن تحدث الحركة الدورية في كل من التربة الرخوة والكثيفة ولكن التشوه يتناقص بشكل ملحوظ مع زيادة الكثافة.
4. يمكن أن يحدث تميع الأرض المستوية عندما يكون التحميل الدوري كافياً لإنتاج ضغوط مسام زائدة عالية، حتى عندما تكون إجهادات القيادة الثابتة غائبة. يتجلى حدوثه عمومًا في تذبذب الأرض، واستقرار ما بعد الزلزال، و/أو تطور غليان الرمل. عادة ما تكون النزوحات الجانبية الدائمة بسبب تميع الأرض المستوية صغيرة. يمكن أن يحدث تميع الأرض المستوية في التربة الرخوة والكثيفة.
5. يتطلب تقييم مخاطر التميع معالجة أسئلة قابلية التميع، والبدء، والآثار. لكي يُعتبر الموقع خاليًا من مخاطر التميع، يجب أن تكون التربة غير قابلة للتميع، ويجب أن يكون التحميل المتوقع غير كافٍ لبدء التميع، أو يجب أن تكون تأثيرات التميع مقبولة.
6. يمكن الحكم على قابلية التميع على أساس الاعتبارات التاريخية والجيولوجية والتركيبية والحالة. يجب استيفاء المعايير الجيولوجية والتركيبية والحالة حتى تكون التربة قابلة للتميع؛ إذا لم يتم استيفاء أي من هذه المعايير، فإن التربة غير قابلة للتميع.
7. تختلف قابلية التميع باختلاف ظواهر التميع. التربة التي تكون قابلة للحركة الدورية أو التميع على مستوى الأرض قد لا تكون قابلة للتميع التدفقي. تعتمد قابلية التميع المختلفة على حالة التربة (ظروف الإجهاد والكثافة) في وقت الزلزال.
8. في ظل ظروف تحميل معينة، سيصل أي رمل إلى تركيبة فريدة من الضغط الحاسم الفعال وقوة القص والكثافة عند إجهادات كبيرة. يمكن وصف التركيبة بيانياً بخط الحالة المستقرة. يتأثر موضع خط الحالة المستقرة بشكل كبير بحجم الحبيبات وخصائص شكل الحبيبات. يرتبط سلوك الرمل ارتباطًا وثيقًا بموقعه بالنسبة لخط الحالة المستقرة.
9. يبدأ تميع التدفق عندما تصل نسبة الإجهاد الفعال الرئيسية إلى قيمة حرجة في ظل ظروف غير مستنزفة وخاضعة للتحكم في الإجهاد. يمكن وصف حالة الإجهاد عند بدء تميع التدفق بيانياً في مساحة مسار الإجهاد بواسطة سطح تميع التدفق. بمجرد وصول مسار الإجهاد الفعال لعنصر من التربة إلى سطح تميع التدفق، فإن الإجهاد الإضافي سيؤدي إلى زيادة ضغط المسام الزائد وستنخفض مقاومة القص المتاحة إلى قوة الحالة المستقرة.
10. لأن حالة الرمل السائب في حالة التوازن تحت إجهاد قص أولي مرتفع أقرب إلى سطح التميع التدفقي من حالة التربة المماثلة المعرضة لإجهاد قص أولي منخفض، فإن ضغط المسام الزائد الأقل مطلوب لبدء التميع التدفقي. يمكن أن يحدث التميع التدفقي بسبب اضطرابات صغيرة غير مصفاة في التربة المعرضة لإجهادات قص أولية عالية. قد تمثل مثل هذه التربة خطرًا كبيرًا للتميع.
11. يمكن أن تنتج الحركة الدورية ضغوطًا زائدة عالية للمسام وإجهادات فعالة منخفضة، لكن الحركة أحادية الاتجاه ستتسبب في تمدد التربة. ستوقف مقاومة القص المتزايدة الناتجة عن التمدد حركة التربة بحيث لا يمكن أن تتطور انزلاقات التدفق.
12. غالبًا ما يُنظر إلى وجود غليان الرمل كدليل على التميع على مستوى الأرض. ومع ذلك، يعتمد تكوين غليان الرمل على عوامل مثل عمق وسمك وحجم الفراغ في الطبقة المسالة وعلى خصائص التربة التي تعلوها.
13. إن نهج الإجهاد الدوري لتقييم إمكانية التميع يميز كل من تحميل الزلزال ومقاومة تميع التربة من حيث الإجهادات الدورية. يتم تحويل حركة الزلزال العابرة إلى سلسلة مكافئة من الدورات المنتظمة لإجهاد القص. يرتبط عدد الدورات المكافئة، وهو دالة على مدة الحركة، بحجم الزلزال. يتم الحصول على مقاومة التميع من الاختبارات المعملية أو في الموقع. تُستخدم عادةً اختبارات القص الثلاثية المحورية والدورية البسيطة في المختبر؛ يتم التعبير عن مقاومة التميع من حيث عدد الدورات المطلوبة لإنتاج فشل تربة ذات كثافة معينة تخضع لمستوى معين من إجهاد القص الدوري. إن مقاومة التميع القائمة على الإجهاد الدوري تتأثر بعوامل مثل نسيج التربة وتاريخ الإجهاد والانفعال والعمر والتي قد تدمرها العينات ويصعب تكرارها في المختبر. إن إجراءات الاختبار في الموقع تميز مقاومة التميع من حيث معلمات الاختبار في الموقع المرتبطة بالتربة التي تحولت إلى سائل في الزلازل السابقة؛ إن مقاومة SPT هي الأكثر استخدامًا، ولكن معلمات أخرى في الموقع، بما في ذلك مقاومة CPT وسرعة موجة القص، تكتسب قبولًا. يسمح نهج الإجهاد الدوري بتقدير عامل الأمان ضد التميع.
14. في نهج الإجهاد الدوري، يتم تمييز حمل الزلزال ومقاومة التميع بالإجهادات الدورية. نظرًا لأن العوامل التي تؤثر على الإجهادات الدورية المطلوبة لبدء التميع لها تأثير مماثل على معامل القص، فإن الإجهاد الدوري (نسبة إجهاد القص الدوري إلى معامل القص) أقل حساسية لها. إن معامل القص هو أحد معاملات مقاومة التميع المهمة في طريقة الإجهاد الدوري. ومن المتوقع حدوث التميع في المواقع التي تكون فيها سعة الإجهاد الدوري المستحثة لعدد معين من الدورات بسبب الزلزال أكبر من سعة الإجهاد الدوري المطلوبة لبدء التميع في نفس عدد الدورات. ولا ينتج عن طريقة الإجهاد الدوري عامل أمان ضد التميع.
15. وقد تم تطوير طرق أخرى لتقييم إمكانية التميع. وقد تم استخدام الطاقة المبددة كمقياس لمقاومة التميع؛ ومقارنتها بمحتوى الطاقة لحركة الأرض تسمح بتقييم إمكانية التميع. ويمكن استخدام تحليلات استجابة الأرض للإجهاد الفعّالة، باستخدام نماذج الإجهاد والانفعال الدورية وضغط المسام أو النماذج التكوينية المتقدمة، للتنبؤ بتوليد ضغط المسام الزائد وإعادة توزيعه أثناء وبعد اهتزاز الزلزال. وتسمح الطرق الاحتمالية، القائمة على نتائج الاختبارات المعملية وملاحظات الأداء الميداني، بتقدير احتمالية التميع.
16. تختلف تأثيرات التميع باختلاف ظواهر التميع. ورغم أن التميع التدفقي قادر على إنتاج التأثيرات الأكثر إثارة، فإن الحركة الدورية والتميع الأرضي المستوي يمكن أن ينتجا أيضًا أضرارًا واسعة النطاق.
17. يمكن أن يؤدي التميع إلى تغيير كبير في سعة ومحتوى التردد لحركات سطح الأرض.
18. قد يتطور ترسيب سطح الأرض أثناء و/أو بعد الزلازل بسبب تكثيف الرمال الجافة أو المشبعة. يحدث ترسيب الرمال الجافة على الفور تقريبًا، لكن ترسيب الرمال المشبعة قد لا يتطور إلا بعد انتهاء اهتزاز الزلزال. يعتمد حجم الترسيب بعد الزلزال على كثافة الرمال وعلى سعة ومدة الاهتزاز.
19. عندما تتجاوز إجهادات القص الناجمة عن الزلزال قوة القص للتربة المسالة، يمكن أن تحدث حالات فشل عدم الاستقرار. يمكن تقييم قوة القص للتربة المسالة من خلال أخذ عينات دقيقة وغير مضطربة واختبارات معملية أو بالمقارنة مع معلمات الاختبار في الموقع والقوى المحسوبة عكسيًا من حالات التميع. تنتج جميع الطرق المتاحة تقديرات للقوة مع قدر كبير من عدم اليقين.
20. تحدث حالات فشل تدفق التميع عندما تتجاوز إجهادات القص الثابتة قوة القص للتربة المسالة. يمكن أن ينشأ هذا الموقف أثناء و/أو بعد الزلزال. يجب التعرف على تأثيرات فك التربة بسبب تدفق مياه المسام على قوة القص وحسابها في تقييم فشل التدفق المحتمل.
21. تتطور حالات فشل التشوه، مثل الانتشار الجانبي، بشكل تدريجي أثناء فترة اهتزاز الزلزال. بالنسبة للمستويات القوية و/أو فترات الاهتزاز الطويلة، يمكن أن تنتج حالات فشل التشوه إزاحات كبيرة وتسبب أضرارًا كبيرة. تم تطوير إجراءات لتقدير الإزاحات الناجمة عن حالات فشل التشوه.

مسائل:

9.1 الرمل المستدير الذي تعرض لسلسلة من اختبارات الضغط الثلاثي المحاور ذات النغمة الرتيبة يظهر خط الحالة المستقرة (SSL) الموضح أدناه. بافتراض أن الرمل يمكنه تحريك زاوية احتكاك 33 درجة في الحالة المستقرة، قم بتقدير قوة الحالة المستقرة التي سيتم تحريكها بواسطة عينات الاختبار التالية:

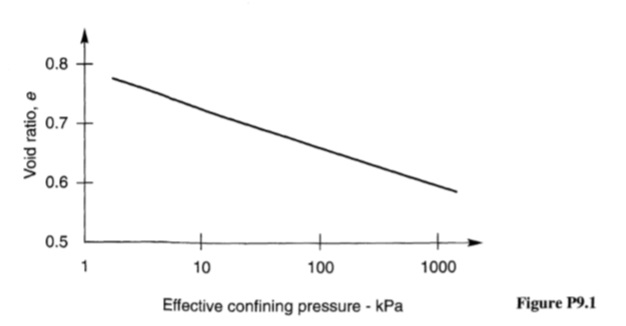
9.2 ضع في اعتبارك عينة اختبار قص بسيط مباشر متماسكة متباينة الخواص مع الظروف الأولية الموضحة أدناه. أظهر بيانياً كيف تكون نسبة ضغط المسام عند بدء التميع r_u,t.

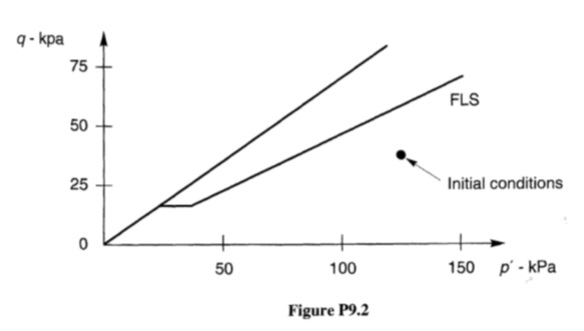
9.3 رواسب رملية سائبة سمكها 10 أمتار مشبعة أسفل عمق 3 أمتار. التربة الموجودة أسفل منسوب المياه الجوفية معرضة بشدة للتميع. قم بتقدير تسارع سطح الأرض المطلوب لإنتاج غليان الرمل في زلزال بقوة M = 7.7.

9.4 قم بتقدير تباين سعة إجهاد القص الدوري المنتظم مع العمق للقدم العلوية 50 من التربة (افترض أن ϒ = 120 pcf) في محطة جيلروي رقم 2 (التربة) في زلزال لوما بريتا قم بتقدير عدد دورات الإجهاد المنتظمة المكافئة.

9.5 تحتوي الرواسب المستوية من الرمل النظيف المشبع على متوسط ​​قيمة (N_l)₆₀ تبلغ 18 ومتوسط ​​وزن الوحدة الجافة 105 pcf. ارسم مخططًا لتغير إجهاد القص الدوري المطلوب لإنتاج التسييل في زلزال M = 5.5 و6.5 و7.5 و8.5.

9.6 كرر المسألة 9.5 على افتراض أن الرمل يحتوي على 15% من الفين.

9.7 ينحدر سطح رواسب سميكة من الرمل الطيني (30% من الفين) بزاوية 10 درجة. تشير اختبارات الاختراق القياسية إلى متوسط ​​((N_l)₆₀=12؛ تشير اختبارات الكثافة إلى متوسط ​​كثافة 1.80 Mg/m³. احسب وارسم إجهاد القص الدوري المطلوب لإنتاج التسييل في 30 قدمًا العلوية من الرمل الطيني في زلزال بقوة M = 7.5.

9.8 رواسب مستوية من الرمل النظيف بنسبة فراغ متوسطة تبلغ 0.70 لها مقاومة طرف CPT غير مصححة تبلغ 80 tsf على عمق 20 قدمًا. يبلغ متوسط ​​حجم حبيبات الرمل 0.40 مم ويبلغ منسوب المياه الجوفية على عمق 4 أقدام. احسب إجهاد القص الدوري المطلوب لإنتاج التسييل على عمق 20 قدمًا في زلزال بقوة M = 6.5.

9.9 قبل في زلزال لوما بريتا عام 1989، أظهر التحقيق في الموقع في قاعدة هانترز بوينت البحرية في سان فرانسيسكو وجود 13 إلى 15 مترًا من الرمال النظيفة المملوءة هيدروليكيًا مع D_S0 = 0.29 مم. وكان منسوب المياه الجوفية على عمق حوالي 2.5 متر. أنتجت اختبارات CPT متوسط ​​مقاومات الطرف التالية:

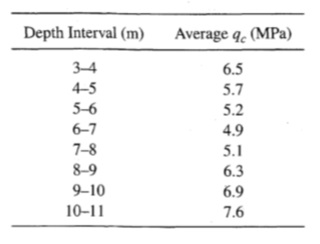
أنتج زلزال لوما بريتا تسارعات أرضية قصوى في حدود 0.15 g إلى 0.20 g في مواقع مماثلة في منطقة الخليج. بافتراض أن متوسط ​​كثافة الرمال الجافة 1.60 Mg/m³، احسب وارسم معامل الأمان ضد التسييل الذي كان متوقعًا في زلزال لوما بريتا.

9.10 ارسم توزيع ضغط المياه المسامية المقدر في نهاية زلزال لوما بريتا في موقع هانترز بوينت الموصوف في المشكلة 9.9.

9.11 كرر المشكلة 9.9 لزلزال بقوة M = 7.6 ينتج عنه تسارع أرضي ذروة يبلغ 0.30 g.

9.12 باستخدام معيار الطاقة الذي وضعه Law et al (1990)، ارسم المسافة المركزية المحدودة التي لن يُتوقع بعدها حدوث تمييع في تربة N₁ = 10 كدالة لحجم الزلزال.

9.13 قدر الاستقرار الرأسي الذي كان متوقعًا في هنترز بوينت (انظر المشكلة 9.9) بعد زلزال لوما بريتا عام 1989.

9.14 قدر وارسم التغير في القوة المتبقية بعد التميع للرمال في الموقع الموصوف في المثال الرابع باستخدام (أ) نهج Seed-Harder، و(ب) نهج Stark-Mesri.

References:

MOGAMI, T., AND KUBU, K. (1953). The behavior of soil during vibration, Proceedings, 3rd International Conference on Soil Mechanics and Foundation Engineering, Zurich, Vol. l, pp. 152-155.

YOUD, T.L. (1984). “Recurrence of liquefaction at the same site,” Proceedings, 8th World Conference on Earthquake Engineering, Vol. 3, pp. 231-238.

YOUD, T.L. (1991). “Mapping of earthquake-induced liquefaction for seismic zonation,” Proceedings, 4th International Conference on Seismic Zonation, Earthquake Engineering Research Institute, Stanford University, Vol. 1, pp. 11 1-147.

AMBRASEYS, N.N. (1988). “Engineering seismology,” Earthquake Engineering and Structural Dynamics, Vol. 17, pp. 1-105.

YOUD, T.L. AND HOOSE, S.N. (1977). ‘.Liquefaction susceptibility and geologic setting,” Proceedings, 6th World Conference on Earthquake Engineering, New Delhi, Vol. 3, pp. 2189-2194.

ISHIHARA, K. (1 984). “Post-earthquake failure of a tailings dam due to liquefaction of the pond deposit,” Proceedings, International Conference on Case Histories in Geotechnical Engineering, University of Missouri, St. Louis, Vol. 3, pp. 1129-1 143.

ISHIHARA, K. (1985). “Stability of natural deposits during earthquakes,” Proceeding, 11th international Conference on Soil Mechanics and Foundation Engineering, Vol. 1, pp. 321-376.

ISHIHARA, K. (1993). Liquefaction and flow failure during earthquakes, Geotechnique, Vol. 43,No. 3, pp. 351-41.

FINN,W .D.L., LEDBETTER, R.H., AND WU, G. (1994). “Liquefaction in silty soils: Design and analysis,” Ground Failures under Seismic Conditions, Geotechnical Special Publication 44, ASCE, New York, pp. 51-76.

COULTER, M. AND MIGLIACCIO, L. (1966). “Effects of the earthquake of March 27, 1964 at Valdez, Alaska.” Professional Paper 542-C, U.S. Geological Survey, U.S. Department of the Interior, Washington, D.C.

CHANG, K.T. (1978). “An Analysis of Damage of Slope Sliding by Earthquake on the Paiho Main Dam and its Earthquake Strengthening,” Tseng-hua Design Section, Dept. of Earthquake-Resistant Design and Flood Control Command of Miyna Reservoir, Peoples Republic of China.

WONG, W. (1984). “Earthquake damages to earth dams and levees in relation to soil liquefaction and weakness in soft clays.” Proceedings, International Conference on Case Histories in Geotechnical Engineering, Vol. 1. pp. 51 1-521.

YOUD, T.L., ET AL. (1985). “The Borah Peak, Idaho earthquake of October 28, 1983–liquefaction,” Earthquake Spectra, Vol. 2, No. 1, pp. 71-89.

YEGIANM, .K., GHARAMAN, V.G., AND HARUTIUNYAN, R.N. (1994). “Liquefaction and embankment failure case histories, 1988 Armenia earthquake,” Journal of Geotechnical Engineering, ASCE, Vol. 120, No. 3, pp. 581-596.

WONG, R.T., SEED, H.B., AKD CHAN, C.K. (197.5). “Liquefaction of gravelly soil under cyclic loading conditions,” Journal of the Geotechnical Engineering Division, ASCE, Vol. 101 NO. GT6, pp. 571c-583.

WONG, W. (1984). “Earthquake damages to earth dams and levees in relation to soil liquefaction and weakness in soft clays.” Proceedings, International Conference on Case Histories in Geotechnical Engineering, Vol. 1. pp. 51 1-521.

EVANS, M.D. AND SEED, H.B. (1987). “Undrained cyclic triaxial testing of gravels: the effect of mem- brane compliance,” Report UCBIEERC-87/08, Earthquake Engineering Research Center, University of California, Berkeley, California.

CASAGRANDE, A. (1936). “Characteristics of cohesion less soils affecting the stability of slopes and earth fills,” Journal of the Boston Society of Civil Engineers, reprinted in Contributions to Soil Mechanics, Boston Society of Civil Engineers, 1940, pp.257-276.

MIDDLEBROOKS, T.A. (1942) “Fort Peck Slide,” Transactions, ASCE, Vol. 107, pp. 723-764.

CASAGRANDE, A, (1976). “Liquefaction and cyclic mobility of sands: a critical review,” Haward Soil Mechanics Series 88, Harvard University, Cambridge, Massachusetts.

CASTRO. G. (1969). “Liquefaction of sands,” Haward Soil Mechanics Series 87, Harvard University, Cambridge, Massachusetts.

ISHIHARA: K., TATSUOKA, F., AND YASLDA, S. (1975). “Undrained deformation and liquefaction of sand under cyclic stresses,” Soils and Foundations, Vol. 15, No. 1, pp. 29-44.

CASTRO, G. AND POIJLOS; S.J. (1977). “Factors affecting liquefaction and cyclic mobility,” Journal of the Geotechnical Engineering Division, ASCE, Vol. 106, NO. GT6, pp. 501-506.

POULOS, S.J. (1981). “The steady state of deformation,” Journal of the Geotechnical Engineering Division, ASCE, Vol. 107, No. GT5, pp. 553-562.

VAID, Y.P., CHUNG, E.K.F., AND KUERBIS, R.H. (1990). “Stress path and steady state,” Canadian Geotechnical Journal, Vol. 27, No. 1, pp. 1-7.

RIEMER, M.F. AND SEED, R.B. (1992). “Observed effects of testing conditions on the residual strength of loose, saturated sands at large strains,” Proceedings, 4th Japan-U.S. Workshop on Earthquake Resistant Design of Lifeline Facilities and Countermeasures for Soil Liquefaction, in M. Hamada and T.D. O’Rourke, eds., Technical Report NCEER-92-0019, National Center for Earthquake Engineering Research, Buffalo, New York, Vol. I, pp. 223-238.

VAID, Y.P. AND THOMAS, J. (1995). Liquefaction and post-liquefaction behavior of sand, Journal of Geotechnical Engineering, ASCE, Vol. 121, No. 2, pp. 163-173.

ROSCOE, K.H. AND POOROSHASB, H.B. (1963)” A fundamental principle of similarity in model tests for earth pressure problems,” Proceedings, 2nd Asian Regional Conference on Soil Mechanics, Tokyo, Vol. 1, pp. 134-140.

BEEN, K. AND JEFFRIES, M.G. (1985). “A state parameter for sands,” Geotechnique, Vol. 35, No. 2, pp. 99-1 12.

BEEK, K., CROOKS, J.H.A., BECKER, D.E., AND JEFFRIES, M.G. (1986). “The cone penetration test in sands; Part I: State parameter interpretation,” Geotechnique, Vol. 36, No. 2, pp. 239-249.

BEEN, K., JEFFERIES, M.G., CROOKS, J.H.A., AND ROTHENBURG, L. (1987). “The cone penetration test in sands, Part 11: General inference of state,” Geotechnique, Vol 37, No. 3, pp. 285-300.

SLADEN, J.A. (1985). “Problems with interpretation of sand state from cone penetration test,” Geo- technique, Vol. 39, No. 2, pp. 323-332.

YU, H.S. (1994). “State parameter from self-boring pressure meter tests in sand,” Journal of Geotechnical Engineering, Vol. 120, No. 12, pp. 21 18-2135.

KONRAD,  J., -M. (1988). “Interpretation of flat plate dilatometer tests in sands in terms of the state parameter,” Geotechnique, Vol. 38, No. 2, pp. 263-278.

ISHIBASHI, I. AND ZHANG, X. (1993). “Unified dynamic shear moduli and damping ratios of sand and clay,” Soils and Foundations, Vol. 33. No. 1. pp. 182-19.

KOPPEJAN, A.W., WAMELAN, B.M. AND WEINBERGL, .J. (1948), “Coastal flow slides in the Dutch Province of Zeeland,” Proceedings, 2nd International Conference on Soil Mechanics and Foundation Engineering, Vol. 5, pp. 89-96.

ANDERSES, A. AND BJERRUM, L. (1968). “Slides in subaqueous slopes in loose sand and silt.” Publication 81, Norwegian Geotechnical Institute, Publication 8, Oslo. pp. 1-9.

BJERRUM, L., (1971). “Subaqueous slope failures in Norwegian fjords,” Publication 88. Norwegian Geotechnical Institute, Oslo.

KRAMER, S.L. AND SEED, H.B. (1988). “Initiation of soil liquefaction under static loading condition,” Journal of Geotechnical Engineering, ASCE, Vol. 114, No. 4, pp. 412-430.

MIDDLEBROOKS, T.A. (1942) “Fort Peck Slide,” Transactions, ASCE, Vol. 107, pp. 723-764.

CORNFORTH, D.H., WORTH, E.G. AND WRIGHTW, .L., (1975). “Observations and analysis of a flow slide in sand fill,” in British Geotechnical Society, Field Instrumentation in Geotechnical Engineering, Wiley, New York, 136-151.

MITCHELL, D.E. (1984). “Liquefaction slides in hydraulically placed sands,” Proceedings, 4th Inter- national Symposium on Landslides, Toronto.

KLEINER, D.E. (1976). “Design and construction of an embankment dam to impound gypsum wastes,” Proceedings, 12th International Congress on Large Dams, International Commission on Large Dams, Mexico City, pp. 235-249.

JENNINGS, J.E. (1979). “The failure of a slimes dam at Bafokeng,” Civil Engineering in South Africa, Vol. 6, pp.135-140.

ECKERSLEYJ.D, . (1985). “Flowslides in stockpiled coal,” Engineering Geology. Vol22, No. I, pp. 13-22. EIBY, G.A. (1980). Earthquakes, Van Nostrand Reinhold, New York.

JAKOBSEN, B. (1952). “The landslide at Surte on the Gota River, September 29, 1952,” Proceedings 5, Royal Swedish Geotechnical Institute, Stockholm.

BROMS, B. AND BENNERMARK, H. (1967). Free discussion, Proceedings, Geotechnical Conference, Val. 2, Oslo, Norway, pp. 118-120.

FELLENIUS, B. (1953). “The landslide at Guntorp,” Geotechnique, Vol. 5, NO. 1, pp. 120-125.

HRYCIWR, .D. (1990). Small-strain-shear modulus of soil by dilatometer, Journal of Geotechnica1 Engineering, ASCE, Vol. 116, No. 11, pp. 1700-1716.

CONLON, R. (1966). “Landslide at Toulnustouc River, Quebec,” Canadian Geotechnical Journal, Val. 3, No. 3, pp. 113-144.

CARTER, D.P. AND SEED, H.B. (1988). “Liquefaction potential of sand deposits under low levels of excitation,” Report UCB/EERC-88/11, Earthquake Engineering Research Center, University of California, Berkeley, 309 p.

HANZAWA, H. , ITOH, Y., AND SUZUKI, K. (1979). “Shear characteristics of a quick sand in the Arabian Gulf,” Soils and Foundations, Vol., 19, No. 4, pp.1-15.

VAID, Y.P. AND CHERN,J .C. (1983). “Effect of static shear on resistance of liquefaction,” Soils and Foundations, Vol. 23, No. 1, pp. 47-60.

VAID,Y .P. AND CHERN, J.C. (1985). “Cyclic and monotonic undrained response of saturated sands,” in V. Khosla ed., Advances in the Art oj Testing Soils under Cyclic Conditions, ASCE, New York, pp. 120-147.

SLADENJ,. A., D’HOLLANDER, R.D., AND KRAHN, J. (1985). “The liquefaction of sands, a collapse surface approach,” Canadian Geotechnical Journal. Vol. 22., No. 4, pp. 564-578.

ISHIHARA, K. (1993). Liquefaction and flow failure during earthquakes, Geotechnique, Vol. 43,No. 3, pp. 351-415.

VAID, Y.P. AND CHERN,J .C. (1983). “Effect of static shear on resistance of liquefaction,” Soils and Foundations, Vol. 23, No. 1, pp. 47-60.

Alarcon-Guzman, A., Leonards, G.A., and Chameau, J.L. (1988). “Undrained monotonic and cyclic strength of sands,” Journal of Geotechnical Engineering, ASCE, Vol. 114, No. 10, pp. 1089-1108.

LADE, P.V. (1992). “Static instability and liquefaction of loose fine sandy slopes,” Journal of Geo- technical Engineering, ASCE, Vol. 1 18, No. 1, pp. 51-71.

CASTRO; G. (1991). “On the behavior of soils during earthquakes – liquefaction.” Proceedings, NSFIEPRI Workshop on Dynamic Soil Porperties and Site Characterization, EPRI NP-7337, Vol. 2, Electric Power Research Institute, Palo Alto, California, pp. 1-36.

CARTER, D.P. AND SEED, H.B. (1988). “Liquefaction potential of sand deposits under low levels of excitation,” Report UCB/EERC-88/11, Earthquake Engineering Research Center, University of California, Berkeley, 309 pp.

DOBRY, R., LADD, R.S., YOKEL, F.Y.. CHUNG, R.M., AKD POWELL, D. (1982). “Prediction of pore water pressure buildup and liquefaction of sands during earthquakes by the cyclic strain method,” NBS Building Science Series 138, National Bureau of Standards, Gaithersburg, Maryland, 150 pp.

MOHAMAD, R. AND DOBRY, R. (1986). “Undrained monotonic and cyclic triaxial strength of sand,” Jorrnal of Geotechnical Engineering, ASCE. Vol. 112, No. 10, pp. 941-958.

SEED, H.B. AND LEE, K.L. (1966). “Liquefaction of saturated sands during cyclic loading,” Journal of the Soil Mechanics and Foundations Division, ASCE, Vol. 92, No. SM6, pp. 105-134.

SEED, H.B., MORI, K.. AND CHAN, C.K. (1975). “Influence of seismic history on the liquefaction characteristics of sands, ” Report EERC 75-25, Earthquake Engineering Research Center, University of California, Berkeley, 21 pp.

HALDAR, A. AND TANG, W.H. (1981). “Statistical study of uniform cycles in earthquakes,” Journal of the Geotechnical Engineering Division, ASCE, VO. 107, NO. GT5, pp. 577-589.

SEED. H.B. AND IDRISS, I.M. (1971). “Simplified procedure for evaluating soil liquefaction potential,” Journal of the Soil Mechanics and Foundations Division, ASCE, Vol. 107, No. SM9, pp. 1249-1274.

PYKE, R., SEED, H.B., AND CHAN, C.K. (1975). “Settlement of sands under multi-directional loading”, Journal of the Geotechnical Engineering Division, ASCE, Vol. 101, No. GT4, pp. 379-398.

SEED, H. B., IDRISS, I. M., MAKDISI, F., AND BANERJEE, N. (1975) “Representation of irregular stress time histories by equivalent uniform stress series in liquefaction analyses”, EERC 75-29, Earthquake Engineering Research Center, University of California, Berkeley.

LEE, K.L. AND ALBAISA, A. (1974). “Earthquake induced settlements in saturated sands, ” Journal of the Soil Mechanics and Foundations Division, ASCE, Vol. 100, NO. GT4.

DEALBA, P., CHAN, C.K., AND SEED, H.B. (1975). “Determination of soil liquefaction characteristics by large-scale laboratory tests,” Report EERC 75-14, Earthquake Engineering Research Center, University of California, Berkeley.

MARTIN, G.R., FINN, W.D.L., AND SEED, H.B. (1975). “Fundamentals of liquefaction under cyclic loading,” Journal of the Geotechnical Engineering Division, ASCE, Vol. 101, NO. GT5, pp. 423-438.

LADD,R .S. (1974). “Specimen preparation and liquefaction of sands,” Journal of the Geotechnical Engineering Division, ASCE, Vol. 100, NO. GTIO, pp. 1180-1 184.

MULILIS, J.P., CHAN, C.K. AND SEED, H.B. (1975). “The effects of method of sample preparation on the cyclic stress-strain behavior of sands,” Report EERC 75-18, Earthquake Engineering Research Center, University of California, Berkeley.

TOKI, S., TATSUOKA, F., MIURA, S., YOSHIMI, Y., YASUDA, S., AND MAKIHARA, Y. (1986). “Cyclic undrained triaxial strength of sand by a cooperative test program.” Soils and Foundations, Vol. 26, NO. 3, pp. 117-128.

TATSUOKA, F., OCHI, K., FUJII, S., AND OKAMOTO. M. (1986). “Cyclic undrained triaxial and torsional shear strength of sands for different sample preparation methods,” Soils and Foundations, Vol. 26, No. 3, pp. 23-41.

FINN, W.D.L., BRANSBY, P.L., AND PICKERING, D.J. (1970). “Effect of strain history on liquefaction of sands,” Journal of the Soil Mechanics and Foundations Division, ASCE, .Vol. 96, NO. SM6, pp. 1917-193.

SEED, H.B., LEE, K.L., IDRISS, I.M., AND MAKDISFI,. I. (1975). “The slides in the San Fernando Dams during the earthquake of February 9, 1971,” Journal of the Geotechnical Engineering Division, ASCE, Vol. 101, No. GT7, pp. 65 1-688.

SEED, H.B. AND PEACOCK, W.H. (197 1). “Test procedures for measuring soil liquefaction characteristics,” Journal of the Soil Mechanics and Foundations Division, ASCE, Vol. 97, No. SM8, pp. 1099-11 19.

SEED, H.B. (1979). Soil liquefaction and cyclic mobility evaluation for level ground during earth- quakes, Journal of the Geotechnical Engineering Division, ASCE, Vol. 105, NO. GT2, pp. 201-255.

OHSAKI, Y. (1969). “The effects of local soil conditions upon earthquake damage,” Proceedings of Specially Session 2, 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City.

YOSHIMI, Y., TOKIMATSU, K., AND HASAKA, Y. (1989). “Evaluation of liquefaction resistance of clean sands based on high-quality undisturbed samples,” Soils and Foundations, Vol. 29, No. 1, pp. 93-104.

WHITMAN, R.V. (1971). “Resistance of soil to liquefaction and settlement,” Soils and Foundations, Vol. 11, No. 4, pp. 59-68.

SEED, H.B., IDRISS, I.M., AND ARANGO, I. (1983). “Evaluation of liquefaction potential using field performance data,” Journal of Geotechnical Engineering, ASCE, Vo. 109, No. 3, pp. 458-482.

SEED, H.B., TOKIMATSU, K., HARDER, L.F., AND CHCNG, R.M. (1985). “Influence of SPT procedures in soil liquefaction resistance evaluations,” Journal of Geotechnical Engineering, Vol. 11 1, No. 12, pp.1425-1445.

ISHIHARA; K. AND KOSEKI, J. (1989). Discussion of “Cyclic shear strength of fines-containing sands.” Earthquake Geotechnical Engineering, 12th International Conference on Soil Mechanics and Foundation Engineering, Rio de Janeiro, pp. 10 1 – 106.

ISHIBASHI, I. AND ZHANG, X. (1993). “Unified dynamic shear moduli and damping ratios of sand and clay,” Soils and Foundations, Vol. 33. No. 1. pp. 182-191.

KOESTER, J.P. (1994). The influence of fines type and content on cyclic strength, Ground Failures Under Seismic Conditions, Geotechnical Special Report No. 44, ASCE, New York, pp. 17-33.

SEED, H.B. (1983). “Earthquake-resistant design of earth dams,” in T.R. Howard, ed., proceedings, Symposium on Seismic Design of Earth Dams, ASCE, New York, pp. 41-64.

ROBERTSON, P.K. AND CAMPANELLA, R.G. (1985). “Liquefaction potential of sands using the CPT,” Journal of Geotechnical Engineering, ASCE, Vol. 11 1, No. 3, pp. 384-403.

SEED, H.B. AND DE ALBA, p. (1986). “Use of SPT and CPT tests for evaluating the liquefaction resistance of soils,” Proceedings, Insitu ’86, ASCE.

MITCHELL, J.K. AND TSENG, D.-J. (1990). “Assessment of liquefaction potential by cone penetration resistance,” in J.M. Duncan ed., Proceedings, H. Bolton Seed Memorial Symposium, Berkeley, California, Vol. 2, pp. 335-350.

MARTIN. G.R. (1992). Evaluation of soil properties for seismic stability analysis of slopes, Proceedings, Stability and Performance of Slopes and Embankments, Geotechnical Special Publication No. 31, ASCE, Vol. 1, pp. 116-142.

DOUGLAS, B.J., OLSEN, R.S., AND MARTIN, G.R. (1981). Evaluation of the cone test for SPT liquefaction assessment, Proceedings, In Situ Testing to Evaluate Liquefaction Susceptibility, ASCE, New York.

KAYEN, R.E., MITCHELL, J.K., SEED, R.B., LODGE, A., NISHIO, S., AND COTINHOR, . (1992). Evaluation of SPT-, CPT-, and shear wave-based methods for liquefaction potential assessment using Loma Prieta data, Proceedings, 4th U.S. – Japan Workshop on Earthquake Resistant Design of Lifeline Facilities and Countermeasures for Soil Liquefaction, Vol. 1, pp. 177-204.

TOKIMATSUK, ., KUWAYAMA, S., AND TAMURA, S. (1991). “Liquefaction potential evaluation based on Rayleigh wave investigation and its comparison with field behavior,” Proceedings, 2nd International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics, St. Louis, Missouri, Vol. 1, pp. 357-364.

FINN, W.D.L. (1991). “Assessment of liquefaction potential and post-liquefaction behavior of earth structures: Developments 1981-1991 (State-of-the-art paper),” Proceedings, 2nd International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics. St. Louis, Missouri, Vol. 3, pp. 1833-1850.

STOKOE, K.H., NAZARIAN, S., RIX, G.J., SANCHEZ-SALINERO, R., SHEU, J.-C., AND MOK, Y.-J. (1988). “In situ seismic testing of hard-to-sample soils by surface wave method,” Proceedings, Earth- quake Engineering and Soil Dynamics 11: Recent Advances in Ground Motion Evaluation, Geotechnical Special Publication 20, ASCE, New York, pp. 264-278.

JAMIOLKOWSKY, M. AND LOPRESTI, D.C.F. (1992). Discussion of “Correlation between liquefaction resistance and shear wave velocity,” by K. Tokimatsu and A. Uchida, Soils and Foundations, Vol. 32, No. 2, pp. 145-148.

VERDUGO, R. (1992). Discussion of “Correlation between liquefaction resistance and shear wave velocity,” by K. Tokimatsu and A. Uchida, Soils and Foundations, Vol. 32, No. 2, pp. 144-145.

MARCHETTI, S. (1982). “Detection of liquefiable sand layers by means of quasi-static penetration tests,” Proceedings, 2nd European Symposium on Penetration Testing, Amsterdam, Vol. 2, pp. 458-482.

ROBERTSOX, P.K. AND CAMPANELLA, R.G. (1986). “Estimating liquefaction potential of sands using the flat dilatometer,” Geotechnical Testing Journal, ASTM, Vol. 9, NO. 1, pp. 38-40.

REYNA, F. AND CHAMEAU, J.-L. (199 1). “Dilatometer based liquefaction potential of sites in the Imperial Valley,” Proceedings, 2nd International Conference on Recent Advances in Geotechnical Earth- quake Engineering and Soil Dynamics, St. Louis, Missouri, Vol. 1, pp. 385-392.

SEED, H.B. (1976). “Some aspects of sand liquefaction under cyclic loading,” Proceedings, Conference on Behavior of Offshore Structures, Norwegian Institute of Technology, Oslo.

DOBRY, R. AND LADD, R.S. (1980). Discussion to “Soil liquefaction and cyclic mobility evaluation for level ground during earthquakes.” by H.B. Seed and “Liquefaction potential: science versus practice,” by R.B. Peck, Journal of the Geotechnical Engineering Division, ASCE, Vol. 106, NO. GT6, pp. 720- 724.

DOBRY, R., LADD, R.S., YOKEL, F.Y.. CHUNG, R.M., AKD POWELL, D. (1982). “Prediction of pore water pressure buildup and liquefaction of sands during earthquakes by the cyclic strain method,” NBS Building Science Series 138, National Bureau of Standards, Gaithersburg, Maryland, 150 pp.

SILVERN, .L. AND SEED,H .B. (1971). “Volume changes in sands during cyclic loading,” Journal of the Soil Mechanics and Foundations Division, ASCE, Vol97, No. SM9.

YOUD, T.L. (1972). “Compaction of sands by repeated shear straining,” Journal of the Soil Mechanics and Foundations Division, ASCE, Vol. 98, NO. SM7, pp. 709-725.

SEED,H .B. (1 980). Closure to “Soil liquefaction and cyclic mobility evaluation for level ground during earthquakes,” Journal of the Geotechnical Engineering Division, ASCE Vol. 106, NO. GT6, p. 724.

DOBRYR, ., MOHAMAD, R., DAKOULAS, P., AND GAZETAS, G. (1984). “Liquefaction evaluation of earth dams – a new approach,” Proceedings, 8th World Conference on Earthquake Engineering, Vol. 3. pp.333-340.

VASQUEZ-HERRERA, A. AND DOBRY, R. (1988). “The behavior of undrained contractive sand and its effect on seismic liquefaction flow failures of earth structures,” Report to U.S. Army Corps of Engineers, Renssalaer Polytechnic Institute, Troy, New York, 510 pp.

NEMAT-NASSER, S. AND SHOKOOH, A. (1979). “A unified approach to densification and liquefaction of cohesionless sand in cyclic shearing,” Canadian Geotechnical Journal, Vol. 16, No. 4, pp. 649-678.

SIMCOCK, K.J., DAVIS,R .O., BERRILL, J.B., AND MULLENGER, G. (1983). “Cyclic triaxial tests with continuous measurement of dissipated energy,” Geotechnical Testing Journal, ASTM, Vol. 6, No. 1, pp. 35-39.

LAW, K.T., CAO, Y.L.. AND HE, G.N. (1990). “An energy approach for assessing seismic liquefaction potential,” Canadian Geotechnical Journal, Vol. 27, NO. 3, pp. 320-329.

FIGUEROAJ.,L . AKD DAHISARIA, N. (1991). “An energy approach in defining soil liquefaction,” Proceedings. 2ndIrzternatio~zal Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics, St. Louis, Missouri, Vol. 1, pp. 407-410.

DAVIS, R.O. AND BERRILL, J.B. (1982). “Energy dissipation and seismic liquefaction in sands,” Earthquake Engineering and Structural Dynamics, Vol. 10, No. 1, pp. 59-68.

MARTIN, G.R., FINN, W.D.L., AND SEED, H.B. (1975). “Fundamentals of liquefaction under cyclic loading,” Journal of the Geotechnical Engineering Division, ASCE, Vol. 101, NO. GT5, pp. 423-438.

ISHIHARA. K. AND TOWHATA, I. (1980). “One-dimensional soil response analysis during earthquakes based on effective stress model,” Journal of the Faculty of Engineering, University of Tokyo, Vol. 35, No. 4.

FINN, W.D.L. AND BHATIA, S.K. (1981). “Prediction of seismic pore-water pressures,” Proceedings, 10th International Conference on Soil Mechanics and Foundation Engineering, Rotterdam, The Netherlands, Vol. 3, pp. 201-206.

MARTIN, G.R., LAM, I.P., MCCASKIE, S.L., AND TSAI, C.-F. (1981). “A parametric study of an effective stress liquefaction model,” Proceedings, International Conference on Geotechnical Earthquake Engineering and Soil Dynamics, St. Louis, Missouri. Vol. 2, pp. 699-705.

PREVOST, J.H. (1989). DYNAlD: a computer program for nonlinear seismic site response analysis – Technical documentation, Report NCEER-89-0025, National Center for Earthquake Engineering Research, Buffalo, New York.

HALDAR, A. AND TANG, W.H. (1979). “Probabilistic evaluation of liquefaction potential,” Journal of the Geotechnical Engineering Division, ASCE, Vol. 105, NO. GT2, pp. 145-163.

FARDIS, M.N. AND VENEZIANO, D. (1982). “Probabilistic analysis of deposit liquefaction,” Journal of the Geotechnical Engineering Division, ASCE, Vol. 108, No. GT3, pp. 395-417.

CHAMEAU, J.L. AND CLOUGH, G.W. (1983). “Probabilistic pore pressure analysis for seismic load- ing,” Journal of Geotechnical Engineering, ASCE, Vol. 109, NO. 4, pp. 507-524.

CHRISTIAN, J.T. AND SWIGER, W.F. (1975). “Statistic of liquefaction and SPT results,” Journal of the Geotechnical Engineering Division, ASCE, Vol. 101, No. GT11, pp. 1135-1 150.

YEGIANM, .K. AND WHITMAN, R.V. (1978). “Risk analysis for ground failure by liquefaction,” Journal of the Geotechnical Engineering Division, ASCE, Vol 104, NO. GT7, pp. 921-938.

VENEZIANOD,. AND LIAO. S. (1984). “Statistical analysis of liquefaction data,” Proceedings, 4th ASCE Specialty Conference on Probabilistic Mechanics and Structural Reliability, pp. 206-209.

LIAO, S.S.C., VENEZIANO, D., AND WHITMAN, R.V. (1988). “Regression models for evaluating liq- uefaction probability,” Journal of Geotechnical Engineering, ASCE, Val. 114, NO. 4, pp. 389-411.

HAMADAM, . AND O’ROURKE, T.D. (1992). Case histories of liquefaction and lifeline performance during past earthquakes, Technical Report NCEER-92-0001, National Center for Earthquake Engineering Research, Buffalo, New York, 2 Vol.

YOUD, T.L. (1993). “Liquefaction-induced lateral spread displacement,” Report TN-1 862, Naval Civil Engineering Laboratory, Port Hueneme, California, 44 pp.

YOUD, T.L. (1984a). “Recurrence of liquefaction at the same site,” Proceedings, 8th World Conference on Earthquake Engineering, Vol. 3, pp. 231-238.

GAO, Z., HO, B., AND CHANG, D. (1983). “Some geological considerations for the damage during the Tangshan earthquake,” North China Earthquake Sciences, Vol. 1, pp. 64-72 (in Chinese).

YOUD, T.L. AND GARRIS, C.T. (1995). Liquefaction-induced ground surface disruption, Journal of Geotechnical Engineering, ASCE, Vol. 121, No. 11, in press.

LIU, H. AND QIAO, T. (1984). “Liquefaction potential of saturated sand deposits underlying foundation of structure,” Proceedings, 8th World Conference on Earthquake Engineering, San Francisco, Val. 3, pp. 199-206.

FIEGEL. G.L. AND KCTTER, B.L. (1992). “The mechanism of liquefaction in layered soils,” Report CR92.009, Naval Civil Engineering Laboratory, Port Hueneme, California, 34 pp.

SEED,H .B. AND SILVER. M.L. (1972). “Settlement of dry sands during earthquakes,” Journal of the Soil Mechanics and Foundations Division, Vol. 98, No. SM4, pp. 381-397.

PYKE, R., SEED, H.B., AND CHAN, C.K. (1975). “Settlement of sands under multi-directional loading,” Journal of the Geotechnical Engineering Division, ASCE, Vol. 101, No. GT4, pp. 379-398.

TOKIMATSC, K. AND SEED, H.B. (1987). “Evaluation of settlements in sand due to earthquake shaking,” Journal of Geotechnical Engineering, ASCE, Vol. 113, NO. 8, pp. 861-878.

OHTA, Y. AND GOTO, N. (1976). Estimation of s-wave velocity in terms of characteristic indices of soil, Butsuri-Tanko, Vol. 29, No. 4, pp. 34-41.

SEED, H.B., TOKIMATSU, K., AND HARDER, L. (1984). “The influence of SPT procedures in evaluating soil liquefaction resistance,” Report UCB/EERC-84-15, Earthquake Engineering Research Center, University of California, Berkeley.

OHSAKI, Y. (1970). “Effects of sand compaction on liquefaction during Tokachioki earthquake,” Soils and Foundations. Vol. 10, No. 2, pp. 112-128.

HEIDARI, M. AND JAMES, R.G. (1982). “Centrifuge modelling of earthquake induced liquefaction in a column of sand,” Proceedings, Conference on Soil Dynamics and Earthquake Engineering, A.A. Balkema, Rotterdam, The Netherlands, Vol. 1, pp. 271-281.

FLORIN, V.A. AND IVANOV, P.L. (1961). “Liquefaction of saturated sand soil,” Proceedings, 5th Inter- national Conference on Soil Mechanics and Foundation Engineering, Paris.

WHITMAN, R.V., LAMBE, P.C., AND AKIYAMA, H. (1982). “Consolidation during dynamic tests on a centrifuge,” Preprint 82-063, ASCE National Convention, Las Vegas, Nevada.

SCOTT, R.F. (1986). “Solidification and consolidation of a liquefied sand column,” Soils and Foundations, Vol. 26, No. 4, pp. 23-31.

POULOS, S.J., CASTRO G., AND FRANCE, J.W. (1985). “Liquefaction evaluation procedure,” Journal of Geotechnical Engineering, ASCE, Vol. 11 1, No. 6, pp. 772-792.

KRAMER, S. L. (1989). “Uncertainty in Steady State Liquefaction Evaluation Procedures,” Journal of Geotechnical Engineering, ASCE, Val. 115, No. 10, pp. 1402-1419.

SEED, H.B. (1986). “Design problems in soil liquefaction,” Journal of Geotechnical Engineering, ASCE, Vol. 113. No. 8, pp. 827-845.

STARK, T.D. AND MESRI, G. (1992). “Undrained shear strength of sands for stability analysis,” Journal of Geotechnical Engineering, ASCE, Vol. 118, No. 11, pp. 1727-1747.

SEED, R.B. AND HARDER, L.F. (1990). “SPT-based analysis of cyclic pore pressure generation and undrained residual strength,” in J.M. Duncan ed., Proceedings, H. Bolton Seed Memorial Symposium, University of California, Berkeley, Vol. 2, pp. 351-376.

VASQUEZ-HERRERA, A,, DOBRY, R., AND BAZIAR, M.H. (1990). “Re-evaluation of liquefaction engineering and flow sliding in the Lower San Fernando Dam during the 1971 earthquake,” Proceedings, 4th U.S. National Conference on Earthquake Engineering, Palm Springs, California, pp. 783-792.

BAZIARM, .H., DOBRY, R., AND ELGAMEL, A.W.M. (1992). “Engineering evaluation of permanent ground deformations due to seismically-induced liquefaction,” Technical Report NCEER-92-0007.

CASTRO, G. AND TRONCOSO, J. (1989). “Effects of 1989 Chilean earthquake on three tailings dams,” Proceedings, 5th Chilean Conference on Seismology and Earthquake Engineering, Santiago, Chile.

FINN, W.D.L., LEDBETTER, R.H., FLEMING; R.L., JR., TEMPLETON, A.E., FORREST, T.W., AND STACY, S.T. (1991). “Dam on liquefiable foundation: Safety assessment and reinediation:” Proceedings, 17th International Conference on Large Dams, Vienna, pp. 531-553.

MARCUSON, W.F. 111, HADALA, P.F., AND LEDBETTER, R.H. (1991). “Seismic rehabilitation of earth dams,” Geotechnical Practice in Dam Rehabilitation, Geotechnical Special Publication 35, ASCE, New York, pp. 430-466.

DEALBA, P. (1983). “Pile settlement in a liquefying soil deposit,” Journal of Geotechnical Engineering, ASCE, Vol. 109, No. 9, pp. 1165-1180.