تحدث الانهيارات الأرضية بشكل منتظم في جميع أنحاء العالم كجزء من التطور المستمر للمناظر الطبيعية. تحدث العديد من الانهيارات الأرضية في المنحدرات الطبيعية، ولكن تحدث أيضًا في المنحدرات التي صنعها الإنسان من وقت لآخر. في أي نقطة زمنية، توجد المنحدرات في حالات تتراوح من مستقرة جدًا إلى مستقرة بشكل ضعيف. عندما يحدث زلزال، غالبا ما تكون تأثيرات اهتزاز الأرض الناجم عن الزلزال كافية للتسبب في فشل المنحدرات التي كانت مستقرة بشكل ضعيف إلى معتدل قبل الزلزال. يمكن أن يتراوح الضرر الناتج من غير مهم إلى كارثي اعتمادا على الخصائص الهندسية والمادية للمنحدر. تسببت الانهيارات الأرضية الناجمة عن الزلازل، والتي تم توثيقها منذ وقت مبكر من عام 1789 قبل الميلاد (Li, 1990)، في كميات هائلة من الدمار عبر التاريخ. في العديد من الزلازل، كانت الانهيارات الأرضية مسؤولة عن قدر أو أكثر من الأضرار التي تسببها جميع المخاطر الزلزالية الأخرى مجتمعة. على سبيل المثال، في زلزال ألاسكا عام 1964، كان ما يقدر بنحو 56% من إجمالي تكلفة الأضرار ناجمًا عن الانهيارات الأرضية الناجمة عن الزلزال (Youd, 1978; Wilson and Keefer, 1985). وجد Kobayashi (1981) أن أكثر من نصف جميع الوفيات في الزلازل الكبيرة (M > 6.9) في اليابان بين عامي 1964 و1980 كانت ناجمة عن الانهيارات الأرضية. أنتج زلزال هاييوان (M = 8.5) عام 1920 في مقاطعة نينغشيا في الصين مئات الانهيارات الأرضية الكبيرة التي تسببت في وفاة أكثر من 100000 شخص (Close and McCormick, 1922). يعد تقييم استقرار المنحدر الزلزالي أحد أهم أنشطة مهندس الزلازل الجيوتقني.
يصف هذا الفصل الأنواع المختلفة من الانهيارات الأرضية الناجمة عن الزلازل والظروف التي تحدث فيها. كما يستعرض المبادئ الأساسية لتقييم استقرار المنحدر، بما في ذلك تحليل الاستقرار الساكن، ثم يقدم عدة طرق لتحليل استقرار المنحدر الزلزالي.
تؤثر العديد من العوامل، بما في ذلك الظروف الجيولوجية والهيدرولوجية، والتضاريس، والمناخ، والعوامل الجوية، واستخدام الأراضي، على استقرار المنحدرات وخصائص الانهيارات الأرضية. وقد تم اقتراح عدد من الإجراءات لتصنيف الانهيارات الأرضية؛ ولعل الإجراء الذي اقترحه Varnes (1978) هو الأكثر استخداما على نطاق واسع في الولايات المتحدة. ويمكن استخدام مبادئ ومصطلحات مماثلة لتصنيف الانهيارات الأرضية الناجمة عن الزلازل (الجدول 10-1) على أساس نوع المادة (التربة أو الصخور)، وطبيعة الحركة (مضطربة أو متماسكة)، وسمات أخرى، مثل السرعة والعمق ومحتوى الماء. ويمكن تقسيم الانهيارات الأرضية الناجمة عن الزلازل إلى ثلاث فئات رئيسية: الانهيارات والانهيارات المضطربة، والانزلاقات المتماسكة، والانتشارات والتدفقات الجانبية. تشمل الانزلاقات والسقوط المتقطع سقوط الصخور، وانزلاقات الصخور، وانهيارات الصخور، وسقوط التربة، وانزلاقات التربة المتقطعة، وانهيارات التربة. يتم قص المواد الأرضية المشاركة في مثل هذه الإخفاقات وكسرها واضطرابها في ترتيب عشوائي تقريبًا. يمكن أن تنتج هذه الأنواع من الإخفاقات، التي توجد عادةً في التضاريس شديدة الانحدار، حركات سريعة للغاية وأضرارًا مدمرة؛ كانت الانهيارات الصخرية وسقوط الصخور تاريخيًا من بين الأسباب الرئيسية للوفاة بسبب الانهيارات الأرضية الناجمة عن الزلازل. تتكون الانزلاقات المتماسكة، مثل انهيارات الصخور والتربة، وانزلاقات الصخور والكتل الترابية، والتدفقات الأرضية البطيئة، عمومًا من عدد قليل من الكتل المتماسكة التي تنتقل أو تدور على أسطح فشل أعمق إلى حد ما في التضاريس شديدة الانحدار إلى المعتدلة. تحدث معظم الانزلاقات المتماسكة بسرعات أقل من الانزلاقات والسقوط المتقطع. تنطوي الانتشارات والتدفقات الجانبية عمومًا على تربة قابلة للتميع، على الرغم من أن الطين الحساس يمكن أن ينتج انهيارات أرضية ذات خصائص متشابهة جدًا. بسبب القوة المتبقية المنخفضة لهذه المواد، يمكن أن يحدث الانزلاق على المنحدرات المسطحة بشكل ملحوظ وينتج سرعات عالية جدًا. تمت مناقشة الانتشارات والانزلاقات التدفقية الناتجة عن التميع بالتفصيل سابقا.
تحدث الأنواع المختلفة من الانهيارات الأرضية الناجمة عن الزلازل بترددات مختلفة. يبدو أن سقوط الصخور وانزلاقات التربة الممزقة وانزلاقات الصخور هي أكثر أنواع الانهيارات الأرضية شيوعًا التي لوحظت في الزلازل التاريخية (الجدول 10-2). الانهيارات الأرضية تحت المائية وتدفقات الأرض البطيئة وانزلاقات الكتل الصخرية والانهيارات الصخرية هي الأقل شيوعًا، على الرغم من أن صعوبة ملاحظة الانهيارات تحت المائية قد تساهم في ندرتها الظاهرة.

الجدول(10.1)

الجدول(10.2)
النشاط الزلزالي الناجم عن الزلازل
في التقييمات الأولية للاستقرار، فإن معرفة الظروف التي حدثت فيها الانهيارات الأرضية الناجمة عن الزلازل في الزلازل السابقة مفيدة. ومن المنطقي أن نتوقع أن مدى النشاط الزلزالي الناجم عن الزلازل يجب أن يزداد مع زيادة قوة الزلزال وأنه قد يكون هناك حد أدنى من القوة نادرًا ما يحدث الانهيار الأرضي الناجم عن الزلازل. ومن المنطقي أيضًا أن نتوقع أن مدى النشاط الزلزالي الناجم عن الزلازل يجب أن ينخفض مع زيادة المسافة بين المصدر والموقع وأنه قد تكون هناك مسافة لا يُتوقع حدوث انهيارات أرضية بعدها في الزلازل ذات الحجم المعين. أظهرت دراسة أجريت على 300 زلزال في الولايات المتحدة بين عامي 1958 و1977 أن أصغر الزلازل التي لوحظ أنها تسببت في انهيارات أرضية كانت قوتها المحلية حوالي 4.0 (Keefer، 1984). تم تقدير الحد الأدنى لأنواع مختلفة من الانهيارات الأرضية كما هو موضح في الجدول 10-3. في الحالات التي لم تتوفر فيها تقديرات للقوة الزلزالية، تم رصد قيم أدنى لشدة ميركالي المعدلة (MMI) وهي IV وV للزلازل المتقطعة أو الانهيارات وأنواع أخرى من الزلال، على التوالي. وعلى الرغم من أن هذه الحدود القائمة على التجارب مفيدة، إلا أنه يجب التعرف على طبيعتها التقريبية؛ حيث يمكن أن يحدث فشل المنحدرات التي تقترب من حافة الفشل في ظل ظروف ثابتة بسبب اهتزازات زلزالية ضعيفة للغاية.

الجدول(10.3)
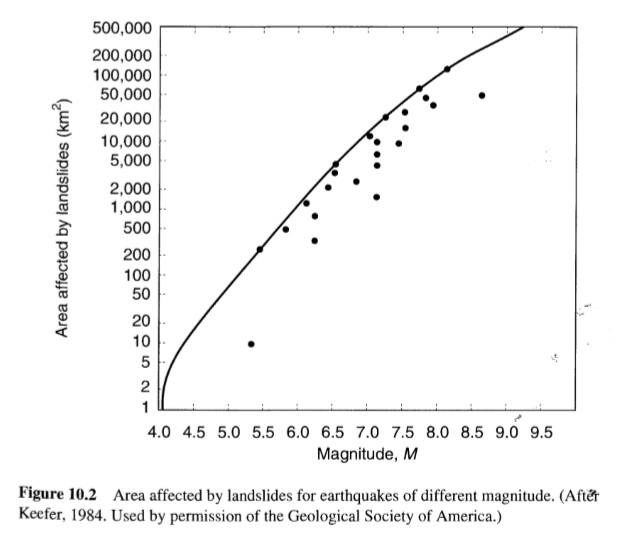
تختلف المسافة القصوى بين المصدر والموقع التي حدثت عندها الانهيارات الأرضية في الزلازل التاريخية باختلاف أنواع الانهيارات الأرضية (الشكل 10.1). على سبيل المثال، نادرًا ما تم العثور على انزلاقات أو سقوطات متقطعة تتجاوز مسافات مركزية تبلغ حوالي 15 كم في أحداث M = 5 ولكن تم رصدها على مسافة تصل إلى حوالي 200 كم (124 ميلًا) في زلازل M = 7. لاحظ أن منحنى الانتشارات والتدفقات الجانبية يرتبط بشكل معقول بمنحنى المقدار والمسافة للتميع. وبالمثل، فإن المنطقة التي يمكن توقع حدوث الانهيارات الأرضية الناجمة عن الزلزال عليها تزداد أيضًا مع زيادة مقدار الزلزال (الشكل 10.2). الاختلافات الإقليمية في سلوك التوهين لها تأثير ضئيل واضح على مساحة الانهيارات الأرضية الناجمة عن الزلزال.
المثال الأول:
قم بتقدير المسافات القصوى التي من المتوقع حدوث انهيارات صخرية وانهيارات تربة وانتشارات جانبية للتربة عند حدوث زلزال بقوة M = 6.5. الحل: تندرج الانهيارات الصخرية، والانهيارات الأرضية، والانتشارات الجانبية للتربة تحت عناوين الانهيارات والانزلاقات المتقطعة، والانزلاقات المتماسكة، والانتشارات والتدفقات الجانبية على التوالي. ومن الشكل 10.1، فإن أقصى مسافات لهذه الأنواع من الانزلاقات من منطقة تمزق الصدع ستكون
انهيار صخري 61 كم انهيارات أرضية 22 كم انتشارات جانبية للتربة 20 كم.
تقييم استقرار المنحدرات:
يتأثر استقرار المنحدرات بالعديد من العوامل، ويجب أن يأخذ تقييم استقرار المنحدر الكامل في الاعتبار تأثيرات كل منها. تؤثر الخصائص الجيولوجية والهيدرولوجية والطوبوغرافية والهندسية والمادية جميعها على استقرار منحدر معين. هناك حاجة إلى معلومات حول هذه الخصائص لأداء وتفسير نتائج تحليلات استقرار المنحدر الساكنة والزلزالية بشكل موثوق. يمكن استخدام مراجعة الوثائق المتاحة، والاستطلاع الميداني، والمراقبة الميدانية، والتحقيق تحت السطح، واختبار المواد للحصول على هذه المعلومات. بالنسبة للعديد من المواقع، يمكن الحصول على معلومات مفيدة كبيرة من الوثائق المنشورة سابقًا مثل الخرائط الجيولوجية، ومسح التربة و/أو الخرائط الزراعية، والخرائط الطبوغرافية، وخرائط المخاطر الطبيعية، وتقارير الهندسة الجيولوجية والجيوتقنية. يمكن الحصول على معلومات إضافية من الصور الجوية (وخاصة الصور الجوية المزدوجة المجسمة) وأشكال أخرى من الاستشعار عن بعد. تتضمن عمليات الاستطلاع الميداني المراقبة الدقيقة والرسم التفصيلي لمجموعة متنوعة من خصائص الموقع المرتبطة بعدم استقرار المنحدر الحالي أو المحتمل. يمكن تحديد ورسم خرائط لخصائص مثل المنحدرات والشقوق الناتجة عن التوتر والانتفاخات والتضاريس المتعرجة والخنادق والقنوات والأسوار المزاحة والأساسات أو الجدران أو الأرصفة المتشققة والأشجار أو الأعمدة المائلة كدليل على عدم الاستقرار. يمكن أن توفر مواقع الجداول والينابيع والتسربات والبرك والمناطق الرطبة والاختلافات في الغطاء النباتي دليلاً على تدفق المياه المتغير أو المنقطع الناجم عن عدم استقرار المنحدر. إذا سمح الوقت، يمكن مراقبة حركة المنحدر. يمكن تثبيت المعالم السطحية في نقاط على المنحدر وبالقرب منه ومسحها بشكل دوري لتحديد حجم واتجاه حركة السطح. يمكن استخدام أساليب التصوير الفوتوغرامتري لتحديد الحركات النسبية من مجموعات من الصور الجوية المزدوجة المجسمة الملتقطة في أوقات مختلفة. تعد أجهزة قياس الميل مفيدة جدًا لمراقبة أنماط التشوه الجانبي تحت سطح الأرض. في كثير من الحالات، يمكن استخدام مقاييس الشقوق، ومقاييس الميل، ومقاييس التمدد لمراقبة تأثيرات حركة المنحدر. عندما تكون ضغوط المسام مهمة، كما هو الحال عادةً، يمكن أن توفر مقاييس الضغط وآبار المراقبة معلومات مهمة عن ضغوط المسام وتغيرها مع الوقت. يمكن أن يشمل التحقيق تحت السطح الحفر ورسم خرائط لحفر الاختبار والخنادق، والحفر وأخذ العينات، والاختبار في الموقع، والاختبار الجيوفيزيائي. يمكن لمثل هذه التحقيقات الكشف عن عمق وسمك وكثافة وقوة وخصائص تشوه الوحدات تحت السطح، وعمق وتغير منسوب المياه الجوفية. تعتبر الاختبارات في الموقع والجيوفيزيائية مفيدة بشكل خاص لتحديد موقع سطح الفشل الحالي. غالبًا ما تستخدم الاختبارات المعملية لقياس الخصائص الفيزيائية للمواد المختلفة تحت السطح لإدخالها في تحليل استقرار المنحدر العددي. تعتبر كثافة التربة وقوتها وسلوك الإجهاد والانفعال ذات أهمية قصوى؛ خصائص أخرى، مثل توزيع حجم الحبيبات، والمرونة، والنفاذية، وقابلية الانضغاط، مفيدة أيضًا. لا يمكن إجراء تحليل الاستقرار إلا بعد الحصول على هذه المعلومات. ورغم أننا نركز في بقية هذا الفصل على أساليب تحليل استقرار المنحدر، فمن المهم أن نتذكر أن التحليل نفسه ما هو إلا جزء واحد من تقييم كامل لاستقرار المنحدر وأن دقته سوف تقل إذا لم يتم إيلاء الاهتمام الدقيق للجوانب الأخرى من التقييم.

الشكل(10.1)
الشكل(10.2)
تحليل استقرار المنحدرات الساكنة
تصبح المنحدرات غير مستقرة عندما تصل أو تتجاوز إجهادات القص المطلوبة للحفاظ على التوازن مقاومة القص المتاحة على بعض أسطح الفشل المحتملة. بالنسبة للمنحدرات التي تكون فيها إجهادات القص المطلوبة للحفاظ على التوازن تحت الحمل الجاذبي الساكن عالية، فقد تكون الإجهادات الديناميكية الإضافية اللازمة لإنتاج عدم الاستقرار منخفضة. وبالتالي فإن الاستقرار الزلزالي للمنحدر يتأثر بشدة باستقراره الساكن. وبسبب هذا وحقيقة أن أكثر الطرق المستخدمة شيوعًا لتحليل الاستقرار الزلزالي تعتمد على تحليلات الاستقرار الساكن، يتم تقديم ملخص موجز لتحليل استقرار المنحدر الساكن. إن إجراءات تحليل استقرار المنحدر في ظل الظروف الساكنة راسخة جيدًا. قدم Duncan (1992) مراجعة ممتازة وموجزة لأحدث التقنيات للتحليل الساكن. يمكن العثور على أوصاف تفصيلية لطرق تحليل محددة في المراجع القياسية مثل National Research Council (1976)، وChowdhury (1978)، وHuang (1983). حاليًا، أكثر الطرق المستخدمة شيوعًا لتحليل استقرار المنحدر الثابت هي تحليلات توازن الحد وتحليلات تشوه الإجهاد.
تحليل توازن الحد:
تأخذ تحليلات توازن الحد في الاعتبار توازن القوة و/أو العزم لكتلة من التربة فوق سطح الفشل المحتمل. يُفترض أن التربة فوق سطح الفشل المحتمل صلبة (أي أن القص يمكن أن يحدث فقط على سطح الفشل المحتمل). يُفترض أن قوة القص المتاحة يتم تحريكها بنفس المعدل عند جميع النقاط على سطح الفشل المحتمل. ونتيجة لذلك، يكون عامل الأمان ثابتًا على سطح الفشل بالكامل. ولأن التربة على سطح الفشل المحتمل يُفترض أنها صلبة – مرنة تمامًا (الشكل 10.3)، فإن تحليلات توازن الحد لا تقدم أي معلومات عن تشوهات المنحدر. عادة ما يتم التعبير عن استقرار المنحدر من حيث مؤشر، وأكثرها شيوعًا هو عامل الأمان، والذي يتم تعريفه عادةً على أنه
FS = available shear strength/ shear stress required to maintain equilibrium
أي قوة القص المتاحة مقسومة على إجهاد القص المطلوب للحفاظ على التوازن، وبالتالي فإن عامل الأمان هو نسبة السعة (قوة القص للتربة) إلى الطلب (إجهاد القص المستحث على سطح الفشل المحتمل). يمكن أيضًا اعتبار عامل الأمان العامل الذي يجب تقسيم قوة التربة به لجلب المنحدر إلى حافة عدم الاستقرار. على النقيض من افتراضات تحليل التوازن الحدي. لا يتم الوصول إلى قوة التربة في المنحدرات الفعلية في نفس الوقت عند جميع النقاط على سطح الفشل، يكون عامل الأمان المحلي غير ثابت).

الشكل(10.3)
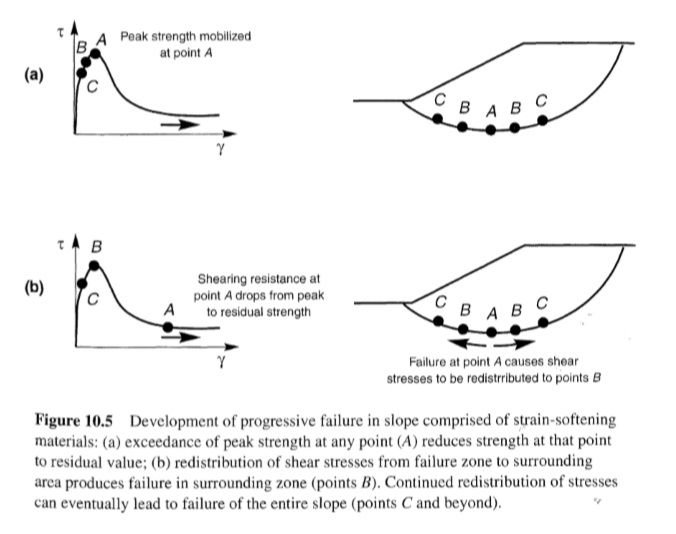
تم تطوير مجموعة متنوعة من إجراءات توازن الحد لتحليل الاستقرار الساكن للمنحدرات. يمكن تحليل المنحدرات التي تفشل على سطح فشل مستو (الشكل 10.4 a) مثل المستوى المبطن أو المفصل الصخري أو التماسات من مادة ضعيفة بسهولة تامة باستخدام طريقة كولمان ((Taylor, 1948. يمكن تحليل المنحدرات التي من المرجح أن يحدث فيها الفشل على مستويين أو ثلاثة مستويات (الشكل 10.4 ب) باستخدام طرق الإسفين (على سبيل المثال، Perloff and Baron، 1976؛ Lambe and Whitman، 1969). في المنحدرات المتجانسة، يكون لسطح الفشل الحرج عادةً شكل دائري (الشكل 10.4 c) أو حلزوني لوغاريتمي. نظرًا لأن الحد الأدنى لعوامل الأمان لأسطح الفشل الدائرية واللولبية اللوغاريتمية متقاربة جدًا، فإن المنحدرات المتجانسة عادةً ما يتم تحليلها بطرق مثل الطريقة العادية للشرائح (Fellenius، 1927) أو طريقة Bishop المعدلة (Bishop، 1955)، والتي تفترض وجود أسطح فشل دائرية. عندما لا تكون الظروف تحت السطح متجانسة (على سبيل المثال، عندما تكون الطبقات ذات قوة مختلفة بشكل كبير، أو قوة متباينة الخواص للغاية، أو توجد انقطاعات)، فمن المرجح أن تكون أسطح الفشل غير دائرية (الشكل 10.4 d). في مثل هذه الحالات، يمكن استخدام طرق مثل تلك التي وضعها Morgenstern and Price ((1965؛ Spencer (1967)؛ Janbu (1968). جميع طرق توازن الحد تقريبًا عرضة للمشكلات العددية في ظل ظروف معينة. تختلف هذه الظروف باختلاف الطرق ولكنها تحدث بشكل شائع عندما تكون التربة ذات قوة تماسك عالية موجودة في أعلى المنحدر أو عندما تظهر أسطح الفشل بشكل حاد عند قاعدة المنحدرات في التربة ذات قوة الاحتكاك العالية (Duncan، 1992). من الناحية النظرية، يجب أن يكون أي منحدر بعامل أمان أعلى من 1.0 مستقرًا. ومع ذلك، في الممارسة العملية، نادرًا ما يُعتبر مستوى الاستقرار مقبولاً ما لم يكن عامل الأمان أكبر بكثير من 1.0. تعترف معايير عوامل الأمان المقبولة (1) بعدم اليقين في الدقة التي يمثل بها تحليل استقرار المنحدر الآلية الفعلية للفشل، (2) عدم اليقين في الدقة التي تُعرف بها معلمات الإدخال (قوة القص، وظروف المياه الجوفية، وهندسة المنحدر، وما إلى ذلك)، (3) احتمالية ومدة التعرض لأنواع مختلفة من التحميل الخارجي، (4) العواقب المحتملة لفشل المنحدر. إن الحد الأدنى النموذجي لعوامل الأمان المستخدمة في تصميم المنحدرات هو حوالي 1.5 لظروف التحميل العادية طويلة الأمد وحوالي 1.3 للمنحدرات المؤقتة أو ظروف نهاية البناء في المنحدرات الدائمة (عندما يؤدي تبديد ضغط المسام إلى زيادة الاستقرار مع الوقت). عندما يصل الحد الأدنى لعامل الأمان لمنحدر إلى قيمة 1.0، يتم تعبئة قوة القص المتاحة للتربة بالكامل على بعض أسطح الفشل المحتملة ويكون المنحدر عند نقطة الفشل الأولي. سيؤدي أي تحميل إضافي إلى فشل المنحدر (أي التشوه حتى يصل إلى تكوين تكون فيه إجهادات القص المطلوبة للتوازن أقل من أو تساوي قوة القص المتاحة للتربة). يشير افتراض التوازن الحدي للسلوك الصلب البلاستيكي تمامًا إلى أن التشوه المطلوب سيحدث بطريقة مطاوعة. ومع ذلك، تظهر العديد من الترب سلوكًا هشًا ومخففًا للإجهاد. في مثل هذه الحالات، قد لا يتم تعبئة قوة القص القصوى في وقت واحد في جميع النقاط على سطح الفشل. عندما يتم الوصول إلى ذروة قوة التربة التي تليين الانفعال، مثل النقطة A في الشكل 10.5 a، فإن مقاومة القص المتاحة سوف تنخفض من الذروة إلى القوة المتبقية. وبينما يحدث هذا، تنتقل إجهادات القص المتعلقة بالفرق بين ذروة وقوة التربة المتبقية عند النقطة A إلى التربة المحيطة. وقد تتسبب إجهادات القص المعاد توزيعها هذه في الوصول إلى قوى الذروة في التربة المحيطة (الشكل 10.5 b) وتجاوزها، وبالتالي تقليل مقاومات القص المتاحة للقيم المتبقية. ومع استمرار عملية إعادة توزيع الإجهاد، قد تنمو منطقة الفشل حتى يصبح المنحدر بأكمله غير مستقر. وقد لوحظت العديد من حالات الفشل التدريجي في تربة تليين الانفعال، حتى عندما يكون عامل التوازن الحدي للسلامة (بناءً على قوة الذروة) أعلى بكثير من 1.0. وفي ظل قيود تحليل التوازن الحدي، يمكن تحليل استقرار المنحدرات مع مواد تليين الانفعال بشكل موثوق فقط باستخدام قوى القص المتبقية. يجب صياغة تحليلات التوازن الحدي بعناية كبيرة. نظرًا لأن مقاومة القص المتاحة للتربة تعتمد على ظروف تصريف مياه المسام، فيجب مراعاة هذه الظروف بعناية عند اختيار قوى القص وظروف ضغط المسام للتحليل. قدم دنكان (1992) إرشادات لاختيار معلمات الإدخال لتحليلات استقرار منحدر التوازن الحدي.

الشكل(10.4)
الشكل(10.5)
تحليلات الإجهاد والتشوه:
تسمح تحليلات الإجهاد والتشوه بدراسة سلوك الإجهاد والانفعال للتربة والصخور، ويتم إجراؤها عادةً باستخدام طريقة العناصر المحدودة. وعند تطبيقها على المنحدرات، يمكن لتحليلات الإجهاد والتشوه التنبؤ بحجم وأنماط الإجهادات والحركات وضغوط المسام في المنحدرات أثناء وبعد البناء/الترسيب. ويمكن النظر في سلوك الإجهاد والانفعال غير الخطي، والظروف الحدودية المعقدة، والأشكال الهندسية غير المنتظمة، ومجموعة متنوعة من عمليات البناء في تحليلات العناصر المحدودة الحديثة. بالنسبة لتحليل استقرار المنحدر الثابت، توفر تحليلات الإجهاد والتشوه مزايا القدرة على تحديد أكثر أنماط الفشل احتمالاً من خلال التنبؤ بتشوهات المنحدر حتى (وفي بعض الحالات بعد) نقطة الفشل، وتحديد المناطق الأكثر إجهاداً داخل المنحدر، والتنبؤ بتأثيرات فشل المنحدر. تأتي هذه المزايا على حساب زيادة وقت الهندسة لصياغة المشكلة، وتوصيف خصائص المواد وتفسير النتائج، وزيادة الجهد الحسابي. إن دقة تحليلات الإجهاد والتشوه تتأثر بشدة بالدقة التي يمثل بها نموذج الإجهاد والانفعال السلوك الفعلي للمادة. وقد تم استخدام العديد من نماذج الإجهاد والانفعال المختلفة لتحليل الإجهاد والتشوه للمنحدرات؛ ولكل منها مزايا وقيود. وعادة ما تقتصر دقة النماذج البسيطة على نطاقات معينة من الانفعال و/أو مسارات إجهاد معينة. وغالبًا ما تكون النماذج التي يمكن تطبيقها على ظروف إجهاد وانفعال أكثر عمومية معقدة للغاية وقد تتطلب عددًا كبيرًا من معلمات الإدخال التي قد يكون من الصعب تحديد قيمها. وبالنسبة للعديد من المشكلات، يقدم النموذج الزائدي ((Kondner, 1963; Kondner and Zelasko, 1963; Duncan and Chang, 1970; Duncan et al., 1980 حلاً وسطًا مناسبًا بين البساطة والدقة.
تحليل استقرار المنحدر الزلزالي:
لقد تم استخدام الإجراءات الموصوفة سابقًا لتحليل استقرار المنحدر الثابت لسنوات عديدة وتم معايرتها ضد العديد من حالات فشل المنحدر الفعلية. إن قاعدة البيانات التي يمكن معايرة تحليلات استقرار المنحدر الزلزالي ضدها أصغر كثيراً. كما أن تحليل الاستقرار الزلزالي للمنحدرات يصبح أكثر تعقيداً بسبب الحاجة إلى النظر في تأثيرات (1) الضغوط الديناميكية الناجمة عن اهتزازات الزلزال، و(2) تأثيرات تلك الضغوط على قوة وسلوك الإجهاد والانفعال لمواد المنحدر. ويمكن تصنيف عدم استقرار المنحدر الزلزالي إلى فئتين على أساس أي من هذه التأثيرات هو السائد في منحدر معين. ففي حالات عدم الاستقرار بالقصور الذاتي، تظل قوة القص للتربة ثابتة نسبياً، ولكن تشوهات المنحدر تنتج عن تجاوزات مؤقتة للقوة بسبب الضغوط الديناميكية للزلزال. أما حالات عدم الاستقرار التي تؤدي إلى إضعاف التربة فهي الحالات التي يعمل فيها الزلزال على إضعاف التربة بدرجة كافية بحيث لا يمكنها أن تظل مستقرة تحت الضغوط الناجمة عن الزلزال. ويعد تميع التدفق والحركة الدورية من الأسباب الأكثر شيوعاً لعدم الاستقرار الذي يؤدي إلى إضعاف التربة. هناك عدد من التقنيات التحليلية، التي تستند إلى كل من تحليلات توازن الحد وتحليلات تشوه الإجهاد، متاحة لكلا فئتي عدم الاستقرار الزلزالي.
تحليل عدم الاستقرار بالقصور الذاتي:
يمكن لحركات الزلازل أن تسبب إجهادات ديناميكية أفقية ورأسية كبيرة في المنحدرات. تنتج هذه الإجهادات إجهادات ديناميكية عمودية وقصية على طول أسطح الفشل المحتملة داخل المنحدر. عند فرضها فوق إجهادات القص الثابتة الموجودة مسبقًا، قد تتجاوز إجهادات القص الديناميكية قوة القص المتاحة للتربة وتنتج عدم استقرار بالقصور الذاتي للمنحدر. تم اقتراح عدد من التقنيات لتحليل عدم الاستقرار بالقصور الذاتي. تختلف هذه التقنيات بشكل أساسي في الدقة التي يتم بها تمثيل حركة الزلزال والاستجابة الديناميكية للمنحدر. تصف الأقسام التالية العديد من الأساليب الشائعة لتحليل عدم الاستقرار بالقصور الذاتي. إن التحليل الأول، وهو التحليل شبه الثابت، ينتج عامل أمان ضد فشل المنحدر الزلزالي بنفس الطريقة التي تنتج بها تحليلات توازن الحد الثابت عوامل أمان ضد فشل المنحدر الثابت. وتحاول جميع الأساليب الأخرى تقييم الإزاحات الدائمة للمنحدر الناتجة عن اهتزازات الزلازل.
التحليل شبه الثابت:
بدءًا من عشرينيات القرن العشرين، تم تحليل الاستقرار الزلزالي للهياكل الأرضية من خلال نهج شبه ثابت حيث يتم تمثيل تأثيرات الزلزال بتسارعات أفقية و/أو رأسية ثابتة. وقد نُسب أول تطبيق صريح للنهج شبه الثابت لتحليل استقرار المنحدر الزلزالي إلى Terzaghi (1950). في أكثر أشكالها شيوعًا، تمثل التحليلات شبه الثابتة تأثيرات اهتزاز الزلزال من خلال تسارعات شبه ثابتة تنتج قوى بالقصور الذاتي، Fh وFv والتي تعمل من خلال مركز كتلة الفشل (الشكل 10.6). تكون أحجام القوى شبه الثابتة هي:
Fh = ah*W/g = kh*W
Fv = av*W/g = kv*W
حيث ah وav، هما تسارعان شبه ثابتان أفقيان ورأسيان، kh و kvهما معاملات شبه ثابتة أفقية ورأسية بلا أبعاد، وW هو وزن كتلة الفشل. يجب أن تكون أحجام التسارعات شبه الثابتة مرتبطة بشدة حركة الأرض المتوقعة؛ إن اختيار التسارعات شبه الثابتة للتصميم، كما تمت مناقشته في القسم التالي، ليس بالأمر البسيط. القوى على كتلة الفشل المحتملة في اتجاه موازٍ لسطح الفشل
FS = resisting force/driving force = [c*lab+[(W-Fv)cosβ-Fh*sinβ]tanφ]/ (W-Fv)sinβ-Fh*cosβ
حيث c وφ هما معلمات قوة موهر-كولومب التي تصف قوة القص على مستوى الفشل و lab هو طول مستوى الفشل. من الواضح أن القوة شبه الثابتة الأفقية تقلل من عامل الأمان – فهي تقلل من قوة المقاومة (لـ (φ > 0) وتزيد من قوة الدفع. عادةً ما يكون للقوة شبه الثابتة الرأسية تأثير أقل على عامل الأمان لأنها تقل (أو تزيد، اعتمادًا على اتجاهها) كل من القوة الدافعة والقوة المقاومة – ونتيجة لذلك، غالبًا ما يتم إهمال تأثيرات التسارع الرأسي في التحليلات شبه الثابتة. يمكن استخدام النهج شبه الثابت لتقييم عوامل الأمان شبه الثابتة لأسطح الفشل المستوية والدائرية وغير الدائرية. تحتوي العديد من برامج الكمبيوتر المتوفرة تجاريًا لتحليل استقرار منحدر التوازن الحد على خيار إجراء تحليلات شبه ثابتة.

الشكل(10.6)
المثال الثاني:
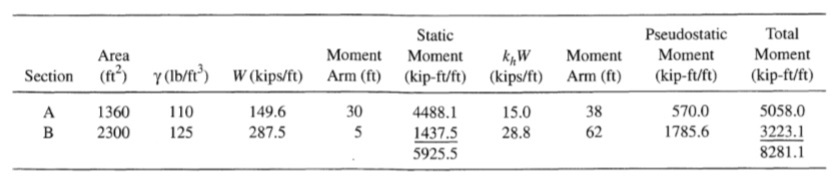
بافتراض أن Kh=0.1 وKv=0.0، احسب عوامل الأمان الساكنة والثابتة الزائفة لمنحدر 2:1 (H:V) بارتفاع 30 قدمًا الموضح في الشكل E10.2. الحل باستخدام تحليل توازن اللحظة البسيط، يمكن تعريف عامل الأمان على أنه نسبة اللحظة التي تقاوم دوران كتلة الفشل المحتملة حول مركز سطح الفشل المحتمل الدائري إلى اللحظة التي تحرك الدوران. يتم تحديد سطح الفشل الحرج، المحدد على أنه السطح الذي يحتوي على أقل عامل أمان، من خلال تحليل عدد من أسطح الفشل المحتملة. فيما يلي حسابات عامل الأمان لسطح فشل محتمل واحد قد يكون أو لا يكون سطح الفشل الحرج. يتطلب حساب عامل الأمان تقييم لحظات الانقلاب والمقاومة لكل من الظروف الساكنة وشبه الساكنة. تنشأ لحظة الانقلاب للظروف الساكنة من وزن التربة فوق سطح الفشل المحتمل. عزم الانقلاب للظروف شبه الثابتة يساوي مجموع عزم الانقلاب للظروف الثابتة وعزم الانقلاب الناتج عن القوى شبه الثابتة. يُفترض أن القوى شبه الثابتة الأفقية تعمل في اتجاهات تنتج عزم دفع موجب (عقارب الساعة، في هذه الحالة). في الحسابات الموضحة، يتم تقسيم التربة فوق كتلة الفشل المحتملة إلى قسمين.
عزم الانقلاب: الجدول(1)
عزم المقاومة: الجدول(2)
عامل الأمان:
Static FS = resisting moment/static overturning moment = 10623.6/5925.5=1.79
Pseudostatic FS = resisting moment/(static + pseudostatic overturning moments) = 10623.6/8281.1 = 1.28
الجدول(1)

الجدول(2)
اختيار المعامل شبه الثابت:
تعتمد نتائج التحليلات شبه الثابتة بشكل حاسم على قيمة معامل الزلازل، kh. إن اختيار معامل استقرار زائف مناسب هو أهم وأصعب جانب في تحليل الاستقرار الزائف. يتحكم معامل الزلازل في القوة الزائفة الساكنة على كتلة الفشل، لذا يجب أن تكون قيمته مرتبطة ببعض مقاييس سعة القوة بالقصور الذاتي المستحثة في المادة غير المستقرة المحتملة. إذا كانت مادة المنحدر صلبة، فإن القوة بالقصور الذاتي المستحثة على انزلاق محتمل ستكون مساوية لحاصل ضرب التسارع الأفقي الفعلي وكتلة المادة غير المستقرة. ستصل هذه القوة بالقصور الذاتي إلى أقصى قيمتها عندما يصل التسارع الأفقي إلى أقصى قيمته. وإدراكًا لحقيقة أن المنحدرات الفعلية ليست صلبة وأن التسارع الأقصى موجود لفترة قصيرة جدًا فقط، فإن معاملات الاستقرار الزائفة المستخدمة في الممارسة العملية تتوافق عمومًا مع قيم التسارع الأقل بكثير من amax. اقترح Terzaghi (1950) في الأصل استخدام kh = 0.1 للزلازل “الشديدة” (روسي-فوريل IX)، وkh = 0.2 للزلازل “العنيفة المدمرة” (روسي-فوريل X)، وkh = 0.5 للزلازل “الكارثية”. وقد أدرج Seed (1979) معايير التصميم شبه الثابت لـ 14 سدًا في 10 دول نشطة زلزاليًا؛ 12 عاملًا مطلوبًا للحد الأدنى من الأمان يتراوح من 1.0 إلى 1.5 مع معاملات شبه ثابتة تتراوح من 0.10 إلى 0.12. واقترح Marcuson (1981) أن المعاملات شبه الثابتة المناسبة للسدود يجب أن تتوافق مع ثلث إلى نصف الحد الأقصى للتسارع، بما في ذلك تأثيرات التضخيم أو إزالة التضخيم، التي يتعرض لها السد. وباستخدام نماذج شعاع القص، أظهر Seed and Martin (1966) وDakoulas and Gazetas (1986) أن القوة بالقصور الذاتي على منحدر غير مستقر محتمل في سد ترابي تعتمد على استجابة السد وأن متوسط معامل الزلازل لسطح الفشل العميق أصغر بكثير من معامل سطح الفشل الذي لا يمتد إلى ما دون القمة. وأشار Seed (1979) أيضًا إلى أن تشوهات السدود الترابية المبنية من تربة مطاوعة (المعرفة بأنها تلك التي لا تولد ضغوطًا عالية للمسام أو تظهر أكثر من 15% من فقدان القوة عند التحميل الدوري) مع التسارعات العظمى أقل من 0.75g ستكون صغيرة بشكل مقبول لعوامل شبه ثابتة للسلامة تبلغ 1.15 على الأقل مع kh=0.10(M = 6.5) إلى kh=0.15(M = 8.25). تسمح هذه المعايير باستخدام تسارعات شبه ثابتة صغيرة تصل إلى 13 إلى 20% من التسارع الأعظمي. طبق Hynes-Griffin and Franklin (1984) تحليل كتلة انزلاق نيومارك على أكثر من 350 مخطط تسارع وخلصوا إلى أن السدود الترابية ذات عوامل الأمان شبه الثابتة الأكبر من 1.0 باستخدام kh = 0.5amax/g لن تتطور تشوهات “كبيرة بشكل خطير”.
كما تشير المناقشة السابقة، لا توجد قواعد صارمة وسريعة لاختيار معامل شبه ثابت للتصميم. ومع ذلك، يبدو من الواضح أن معامل شبه الثابت يجب أن يستند إلى المستوى الفعلي المتوقع للتسارع في كتلة الفشل (بما في ذلك أي تأثيرات تضخيم أو إزالة تضخيم) وأنه يجب أن يتوافق مع جزء من تسارع الذروة المتوقع. على الرغم من أن الحكم الهندسي مطلوب في جميع الحالات، فإن معايير Hynes-Griffin and Franklin (1984) يجب أن تكون مناسبة لمعظم المنحدرات.
حدود النهج شبه الثابت:
من الواضح أن تمثيل التأثيرات الديناميكية المعقدة والعابرة لهزات الزلزال من خلال تسارع شبه ثابت أحادي الاتجاه ثابت أمر بدائي للغاية. حتى في بداياته، تم التعرف بوضوح على حدود النهج شبه الثابت. وقد ذكر Terzaghi (1950) أن “المفهوم الذي ينقله عن تأثيرات الزلازل على المنحدرات غير دقيق للغاية، على أقل تقدير”، وأن المنحدر قد يكون غير مستقر حتى لو كان عامل الأمان شبه الثابت المحسوب أكبر من 1. وقد أوضحت التحليلات التفصيلية للانهيارات الأرضية الناجمة عن الزلازل التاريخية والحديثة (على سبيل المثال، Seed et al، 1969، 1975؛Marcuson et al ، 1979) أوجه قصور كبيرة في النهج شبه الثابت. فقد أظهرت التجربة بوضوح، على سبيل المثال، أن التحليلات شبه الثابتة قد تكون غير موثوقة للتربة التي تتراكم فيها ضغوط مسام كبيرة أو تظهر أكثر من حوالي 15% تدهور في القوة بسبب اهتزاز الزلزال. وكما هو موضح في الجدول 10-4، أنتجت التحليلات شبه الثابتة عوامل أمان أعلى بكثير من 1 لعدد من السدود التي فشلت لاحقًا أثناء الزلازل. إن هذه الحالات توضح عدم قدرة الطريقة شبه الثابتة على تقييم استقرار المنحدرات المعرضة لعدم الاستقرار المضعف بشكل موثوق. ومع ذلك، فإن الطريقة شبه الثابتة يمكن أن توفر على الأقل مؤشرًا أوليًا للاستقرار النسبي، إن لم يكن مطلقًا.
المناقشة: تتميز الطريقة شبه الثابتة بعدد من الميزات الجذابة. التحليل بسيط ومباشر نسبيًا؛ والواقع أن تشابهه مع تحليلات توازن الحد الثابت التي يجريها مهندسو الجيوتقنية بشكل روتيني يجعل حساباته سهلة الفهم والأداء. إنه ينتج مؤشرًا قياسيًا للاستقرار (عامل الأمان) مشابهًا للمؤشر الناتج عن تحليلات الاستقرار الثابت. ومع ذلك، يجب أن ندرك دائمًا أن دقة الطريقة شبه الثابتة تحكمها الدقة التي تمثل بها القوى شبه الثابتة البسيطة القوى الديناميكية المعقدة بالقصور الذاتي الموجودة بالفعل في الزلزال. إن الصعوبة في تعيين معاملات شبه ثابتة مناسبة وفي تفسير عوامل شبه ثابتة للسلامة، إلى جانب تطوير أساليب تحليل أكثر واقعية، قد قللت من استخدام النهج شبه الثابت لتحليل استقرار المنحدر الزلزالي. إن الأساليب القائمة على تقييم تشوه المنحدر الدائم، مثل تلك الموضحة في الأقسام التالية، تُستخدم بشكل متزايد لتحليل استقرار المنحدر الزلزالي.

الجدول(10.4)
تحليل كتلة انزلاق نيومارك:
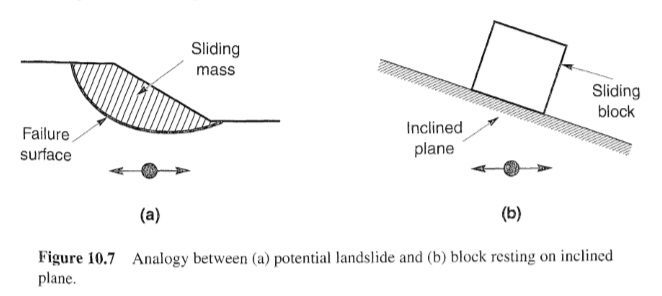
إن الطريقة شبه الثابتة للتحليل، مثل جميع طرق التوازن الحدية، توفر مؤشرًا للاستقرار (عامل الأمان) ولكنها لا توفر أي معلومات عن التشوهات المرتبطة بفشل المنحدر. ونظرًا لأن صلاحية المنحدر بعد الزلزال يتم التحكم فيها عن طريق التشوهات، فإن التحليلات التي تتنبأ بنزوح المنحدر توفر مؤشرًا أكثر فائدة لاستقرار المنحدر الزلزالي. ونظرًا لأن التسارع الناجم عن الزلزال يتغير مع الوقت، فإن عامل الأمان شبه الثابت سيتغير طوال الزلزال. وإذا أصبحت القوى بالقصور الذاتي المؤثرة على كتلة الفشل المحتملة كبيرة بما يكفي بحيث تتجاوز القوى الدافعة الكلية (الثابتة بالإضافة إلى الديناميكية) قوى المقاومة المحتملة، فإن عامل الأمان سينخفض إلى أقل من 1.0. وقد درس Newmark (1965) سلوك المنحدر في ظل مثل هذه الظروف. فعندما يكون عامل الأمان أقل من 1.0 لم تعد كتلة الفشل المحتملة في حالة توازن، وبالتالي سوف تتسارع بسبب القوة غير المتوازنة. إن الموقف مشابه لموقف كتلة ترتكز على مستوٍ مائل الشكل 10.7. استخدم نيومارك هذا القياس لتطوير طريقة للتنبؤ بالإزاحة الدائمة لمنحدر معرض لأي حركة أرضية.
لنفترض أن الكتلة في حالة توازن ثابت في المكان المائل الموضح في الشكل 10.7 b. في ظل ظروف ثابتة. يتطلب توازن الكتلة (في الاتجاه الموازي للمستوى) أن تتجاوز قوة المقاومة الساكنة المتاحة، Rs، قوة الدفع الساكنة Ds (الشكل 10.8 a) بافتراض أن مقاومة الكتلة للانزلاق هي احتكاكية بحتة (c = 0).
FS = available resisting force/static driving force = Rs/Ds = Wcosβtanφ/Wsinβ = tanφ/tanβ
حيث φ هي زاوية الاحتكاك بين الكتلة والمستوى. الآن ضع في اعتبارك تأثير القوى بالقصور الذاتي التي تنتقل إلى الكتلة عن طريق الاهتزاز الأفقي للمستوى المائل مع التسارع، ah(t) = kh(t)g (سيتم إهمال تأثيرات التسارع الرأسي من أجل التبسيط). في لحظة معينة من الزمن، سيتسبب التسارع الأفقي للكتلة في إحداث قوة بالقصور الذاتي الأفقية، khW (الشكل 10.8 b). عندما تعمل القوة بالقصور الذاتي في اتجاه المنحدر، فإن القوى الحاسمة العمودية على المستوى المائل تعطي
FSd(t) = available resisting force/pseudostatic driving force = Rd(t)/Dd(t) = [cosβ-kh(t)sinβ]tanφ/ (sinβ+kh(t)cosβ)
من الواضح أن عامل الأمان الديناميكي يتناقص مع زيادة kh وسيكون هناك (بالنسبة للكتلة المستقرة بشكل ثابت) بعض القيم الإيجابية لـ kh والتي ستنتج عامل أمان يبلغ 1.0 (الشكل 10.9). يتوافق هذا المعامل، المسمى معامل الخضوع، ky، مع ارتفاع تسارع الخضوع، ay = kyg. تسارع الخضوع هو الحد الأدنى من التسارع شبه الثابت المطلوب لإنتاج عدم استقرار الكتلة. بالنسبة للكتلة الموضحة في الشكل 10.8،
ky = tan(φ – β)
للانزلاق في اتجاه المنحدر. للانزلاق في اتجاه المنحدر (الذي يمكن أن يحدث عندما تكون قيمتا β وφ صغيرتين)،
ky = tanφ + tanβ/(1+tanφtanβ)
المثال الثالث:
احسب تسارع الخضوع للمنحدر الموضح في المثال الثاني. الحل يمكن حساب تسارع الخضوع عن طريق التجربة والخطأ، أو حسابه مباشرة للمنحدرات البسيطة نسبيًا. بمراجعة المثال 10.2، من الواضح أن عزم الدوران الكلي يساوي:
Mt = 4488 k-ft/ft + kh(5685 k-ft/ft) + 1438 k-ft/ft + kh(17825 k-ft/ft) = 5926 k-ft/ft + kh(23510 k-ft/ft)
معامل الخضوع هو قيمة kh التي تنتج عامل أمان شبه ثابت 1. ولأن عزم المقاومة يساوي عزم الانقلاب عندما FS = 1،
5926 k-ft/ft + kh(23510 k-ft/ft) = 10624 k-ft/ft
أي:
Kh = 0.20
لذلك، فإن تسارع الخضوع هو 0.20g.
الشكل(10.7)

الشكل(10.8)

الشكل(10.9)
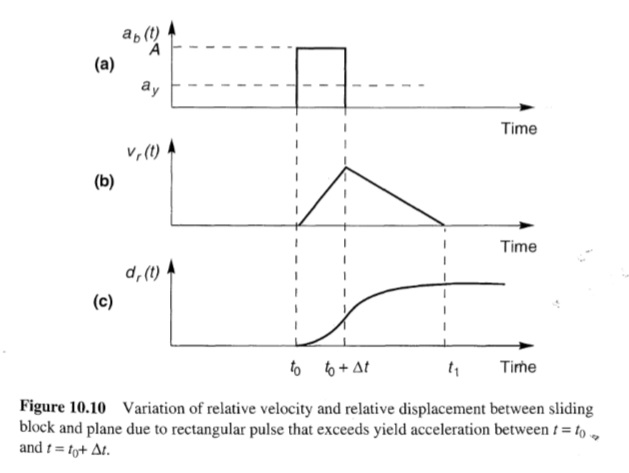
عندما تتعرض كتلة على مستوى مائل لنبضة تسارع تتجاوز تسارع الخضوع، تتحرك الكتلة بالنسبة للمستوى. ولتوضيح الإجراء الذي يمكن من خلاله حساب الإزاحات الدائمة الناتجة، ضع في اعتبارك الحالة التي يخضع فيها المستوى المائل لنبضة تسارع مستطيلة واحدة بسعة A ومدتها Δt. إذا كان تسارع الخضوع، ay أقل من A (الشكل 10.10 a)، فإن تسارع الكتلة بالنسبة للمستوى خلال الفترة من t0 إلى t0+Δt هو
arel(t) = ab(t)-ay = A-ay t0<=t<=t0+Δt
حيث ab(t) هو تسارع المستوى المائل. ويمكن الحصول على الحركة النسبية للكتلة خلال هذه الفترة من خلال تكامل التسارع النسبي مرتين، أي.
vrel(t) = ꭍ arel(t) dt = [A-ay](t-t0) t0<=t<=t0+Δt
drel(t) = ꭍ vrel(t) dt = [A-ay](t-t0)2/2 t0<=t<=t0+Δt
عند t = t0+ Δt، تصل السرعة النسبية إلى أقصى قيمتها. في ذلك الوقت
= [A-ay]Δt vrel(t0+Δt)
drel(t0+Δt) =(1/2)[A-ay]Δt2
بعد أن ينخفض تسارع القاعدة إلى الصفر (عند t0+Δt t=)، تتباطأ كتلة الانزلاق بفعل قوة الاحتكاك المؤثرة على قاعدتها. ستستمر الكتلة في الانزلاق على المستوى، ولكن بسرعة متناقصة تصل في النهاية إلى الصفر. يُعطى التسارع خلال هذا الوقت بواسطة:
arel(t)=ab(t) – ay= 0- ay = -ay t0 +Δt <=t<=tl
حيث tl هو الوقت الذي تصبح فيه السرعة النسبية صفرًا (لاحظ أن الكتلة تخضع لتسارع سلبي، أو تباطؤ، خلال هذه الفترة). بين t0 +Δt و tl ستنخفض السرعة النسبية مع الوقت وفقًا لـ
vrel(t) = A Δt – ay(t- t0) t0 +Δt <=t<=tl
ضبط السرعة النسبية على صفر عند t = tl يعطي
tl = t0 + A Δt/ ay
عندئذ:
drel(t) = A Δt(t- t0– Δt)-(1/2)[t2-(t0+ Δt)2] t0 +Δt <=t<=tl
بعد الوقت tl تتحرك الكتلة والمستوى المائل معًا. وخلال الفترة الزمنية الإجمالية بين t= t0 إلى و t=tl تكون الحركة النسبية للكتلة كما هو موضح في الشكل 10.10. بين t0 و t0+Δtتزداد السرعة النسبية خطيًا والإزاحة النسبية تربيعيًا. عند t0+Δt تصل السرعة النسبية إلى أقصى قيمتها، وبعد ذلك تنخفض خطيًا. تستمر الإزاحة النسبية في الزيادة (ولكن بمعدل متناقص) حتى t= tl لاحظ أن الإزاحة النسبية الكلية
drel(tl) = (1/2)(A-ay)Δt2(A/ay)
تعتمد بشدة على كل من المقدار الذي يتم به تجاوز تسارع الخضوع وطول الوقت الذي يتم خلاله تجاوز تسارع الخضوع. ويشير هذا إلى أن الإزاحة النسبية الناجمة عن نبضة واحدة من حركة الأرض القوية يجب أن تكون مرتبطة بكل من سعة ومحتوى التردد لتلك النبضة. ومع ذلك، يمكن لحركة الزلزال أن تتجاوز تسارع الخضوع عدة مرات وتنتج عددًا من الزيادات في الإزاحة (الشكل 10.11). وبالتالي فإن الإزاحة الكلية ستتأثر بمدة الحركة القوية بالإضافة إلى محتوى السعة والتردد. والواقع أن تطبيق هذا النهج على مجموعة متنوعة من أشكال الموجة البسيطة (على سبيل المثال، Sarma، 1975؛ Yegian et al، 1991) أظهر أن الإزاحة الدائمة لكتلة منزلقة معرضة لحركات قاعدية دورية مستطيلة وجيبية ومثلثة تتناسب مع مربع فترة الحركة القاعدية.
الشكل(10.10)

الشكل(10.11)
تأثير تسارع الخضوع على إزاحات المنحدر:
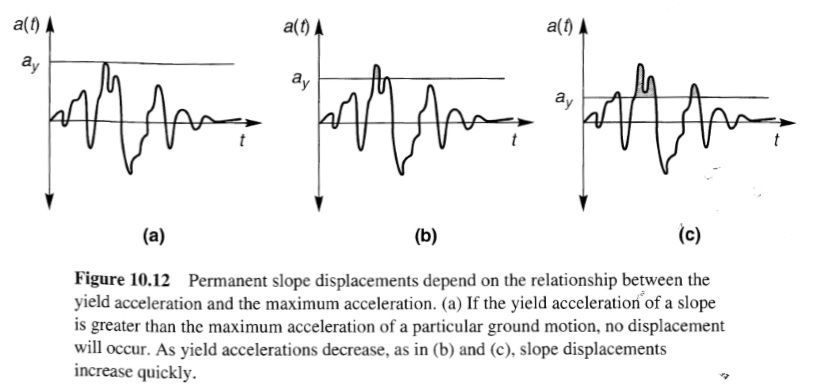
من الواضح أن نموذج كتلة الانزلاق سيتنبأ بإزاحة دائمة للمنحدر تساوي صفرًا إذا لم تتجاوز التسارعات الناجمة عن الزلزال تسارع الخضوع (ay/amax>= 1.0) كما هو موضح في الشكل 10.12 a. ونظرًا لأن الإزاحة الدائمة يتم الحصول عليها من خلال التكامل المزدوج للتسارع الزائد، فإن الإزاحات المحسوبة لمنحدر ذي تسارع خضوع منخفض نسبيًا (ay/amax صغير) ستكون أكبر من تلك الخاصة بمنحدر ذي تسارع خضوع أعلى (الشكل 10.12 b، c). وقد قام عدد من الباحثين بالتحقيق في العلاقة بين إزاحة المنحدر وay/amax.
باستخدام حل النبضة المستطيلة الذي تم تطويره، ربط Newmark (1965) إزاحة منحدر النبضة المفردة بسرعة القاعدة القصوى، vmax بواسطة:
drel= (v2max/2ay)[(1-ay)/A]
اقترح تحليل العديد من حركات الزلازل المعيارية للتسارع الأعظمي البالغ 0.5g والسرعات الأعظمية البالغة (76 سم/ثانية) أنه يمكن تقريب العدد الفعال للنبضات في حركة الزلزال بواسطة A/ay. وجد نيومارك أن الحد الأعلى المعقول للإزاحات الدائمة الناتجة عن حركات الزلزال هذه تم إعطاؤه بواسطة:
dmax=v2maxamax/2a2y
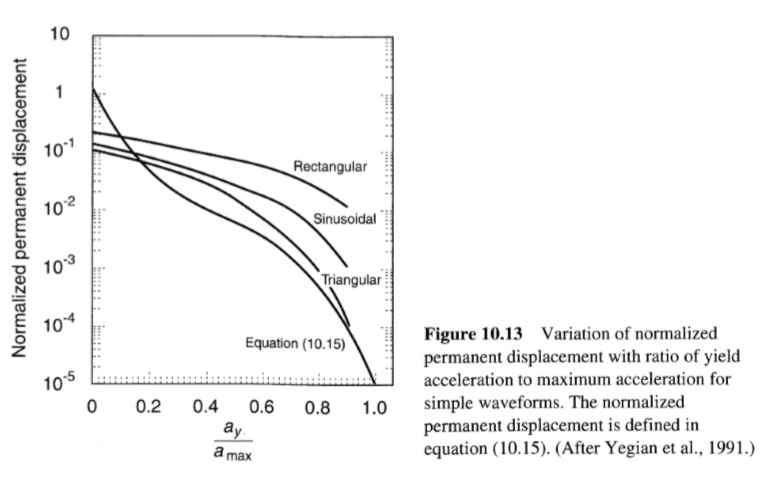
حيث ay/amax>=0.17. استنتج سارما (1975) وييجيان وآخرون (1988) حلولاً مغلقة الشكل للإزاحات الدائمة الناتجة عن حركات الإدخال الدورية البسيطة (المثلثة والجيبية والمستطيلة) (الشكل 10.13). تُظهر دراسات النزوح الدائم التي تنبأت بها طريقة كتلة الانزلاق لحركات الزلازل الفعلية (على سبيل المثال، Sarma، 1975؛ Franklin and Chang، 1977؛ Makdisi and Seed، 1978؛ Ambraseys and Menu، 1988) أشكالًا مماثلة لتلك الخاصة بالموجات الجيبية والمثلثة عند قيم ay/amax، أكبر من حوالي 0.5. وجد Ambraseys and Menu (1988) أن الشكل عند قيم ay/amax الأصغر يتأثر بما إذا كانت الحركات الصاعدة قد تم أخذها في الاعتبار أم لا؛ وفي الحالة التي لم يتم أخذها في الاعتبار، تم إعطاء النزوح الدائم (بالسنتيمترات) الناجم عن الحركات الأرضية الفعلية بواسطة:
Log u= 0.9+log[(1-ay/amax)2.53(ay/amax)-1.09] σlog u=0.3
من أجل 0.1=<ay/amax<=0.9 و6.6=<Ms<=7.3 وay محسوبة باستخدام قوة التربة المتبقية. للسماح بأخذ مقاييس محتوى التردد والمدة في الاعتبار بشكل صريح Yegian et al (1991) استخدم قاعدة بيانات Franklin and Chang (1977) لتطوير التعبير التالي للنزوح الطبيعي الدائم المتوسط:
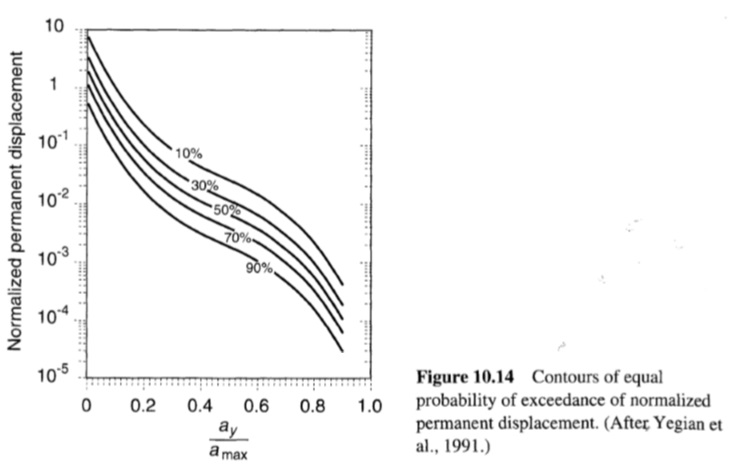
log u= log(u/amaxNeqT2)
حيث Neq هو عدد مكافئ من الدورات وT هي الفترة السائدة. مع الأخذ في الاعتبار مصدر عدم اليقين هذا فقط، يمكن تحديد احتمالات تجاوز الإزاحات المختلفة (الشكل 10.14). قدم Constantinou and Gazetas (1984) وLin and Whitman (1986) طرقًا بديلة للتحليل الاحتمالي لإزاحات المنحدر. أدى الاعتراف بحدود تسارع الذروة كوصف وحيد للحركة الأرضية القوية إلى استخدام معلمات حركة أرضية أخرى في التنبؤ بإزاحة المنحدر. تم ربط إزاحات الكتلة المنزلقة بشدة:
– 6.642 ay + 1.546 σlog u=0.409 log u= 1.46 log Ia
حيث u بالسنتيمتر، وIa، بالسنتيمتر/ ثانية، وay بالـ g (Jibson، 1994) ويستخدم للتنبؤ بالحدود المساحية للانهيارات الأرضية الناجمة عن الزلازل (Wilson and Keefer، 1985). إن جانبين من جوانب استقرار المنحدر الزلزالي يتم توضيحهما بوضوح من خلال الدراسات الموصوفة في الفقرات السابقة. أولاً، إن إزاحات المنحدر الناجمة عن الزلازل حساسة للغاية لقيمة تسارع الخضوع. وبالتالي، فإن الاختلافات الصغيرة في تسارع الخضوع يمكن أن تنتج اختلافات كبيرة في إزاحة المنحدر المتوقعة. ثانياً، إن التباين الكبير في توزيعات سعات نبضات التسارع بين حركات الأرض المختلفة ينتج تباينًا كبيرًا في إزاحات المنحدر المتوقعة. حتى حركات الأرض ذات السعات ومحتويات التردد والمدد المماثلة يمكن أن تنتج إزاحات منحدر متوقعة مختلفة بشكل كبير. يجب إدراك هذا عدم اليقين في التنبؤ بتشوهات المنحدر الناجمة عن الزلازل.
المثال الرابع:
قم بتقدير الإزاحة الدائمة المتوقعة للمنحدر الموصوفة في المثال الثالث إذا تعرضت لحركة أرضية تعادل حركة زلزال جيلروي رقم 1 (الصخرية). استخدم إجراءات نيومارك وجيبسون.
الحل من المثال الثالث فإن التسارع الأعظمي وسرعة حركة جيلروي رقم 1 (الصخرة) هما
amax=0.442g
vmax= 33.7cm/s
تم حساب تسارع الخضوع على أنه 0.20g في المثال الثالث. بعد ذلك، باستخدام إجراء نيومارك، سيكون تقدير الحد الأعلى للإزاحة الدائمة هو
dmax = 33.7*0.442/2*0.2*981*0.2 = 6.4 cm
تم حساب شدة أرياس لحركة جيلروي رقم 1 (الصخرة) على أنها Ia= 167.7 cm/s. باستخدام إجراء جيبسون، يمكن الحصول على الإزاحة الدائمة المتوسطة بواسطة:
log u = 1.4601og(1.677) – 6.642(0.20) + 1.546 = 0.545
أي u= 3.5 cm
حركات الإدخال:
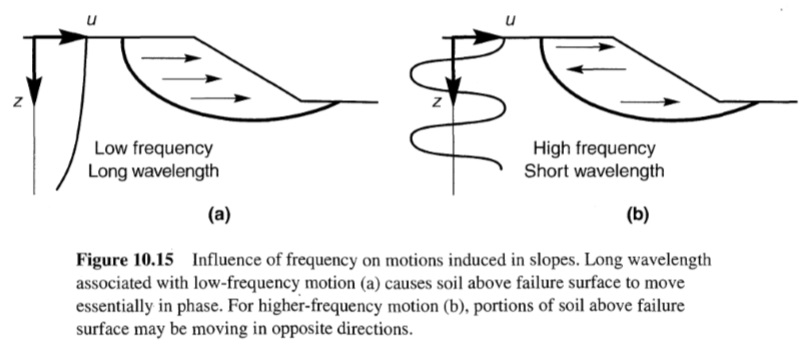
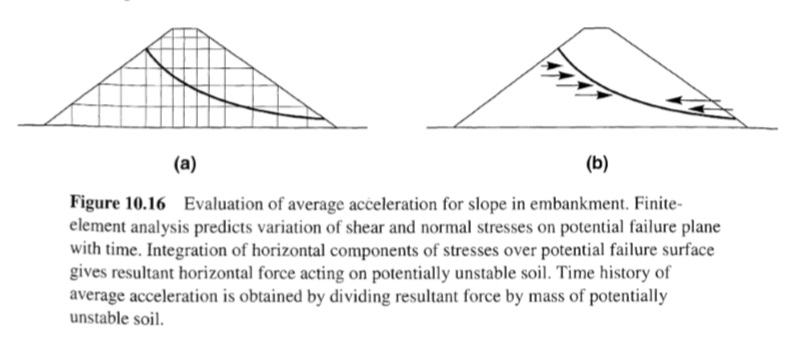
تعتمد دقة تحليل كتلة الانزلاق على دقة حركة الإدخال المطبقة على المستوى المائل. وكما هو مقترح في الأصل، تفترض طريقة كتلة الانزلاق أن كتلة الفشل المحتملة صلبة، وفي هذه الحالة تكون حركة الإدخال المناسبة هي حركة الأرض عند مستوى سطح الفشل. ومع ذلك، فإن المنحدرات الفعلية متوافقة – فهي تتشوه أثناء اهتزاز الزلزال. وتعتمد استجابتها الديناميكية على هندستها وصلابتها وعلى محتوى سعة وتردد حركة الأرض الأساسية. بالنسبة للمنحدرات المكونة من تربة شديدة الصلابة و/أو المنحدرات المعرضة لحركة منخفضة التردد (تركيبة تنتج أطوال موجية طويلة)، فإن الإزاحات الجانبية في جميع أنحاء كتلة الفشل المحتملة ستكون في نفس الطور تقريبًا (الشكل 10.15 a) وسيتم استيفاء افتراض الكتلة الصلبة على الأقل تقريبًا. ومع ذلك، قد تكون الإزاحات الجانبية في كتل الفشل المحتملة للمنحدرات في التربة الأكثر ليونة (و/أو المنحدرات المعرضة لحركة ذات تردد أعلى) خارج الطور (الشكل 10.15 b). عندما يحدث هذا، قد تعمل القوى بالقصور الذاتي عند نقاط مختلفة داخل كتلة الفشل المحتملة في اتجاهات متعاكسة وقد تكون القوة بالقصور الذاتي الناتجة أصغر بكثير من تلك التي يفترضها افتراض الكتلة الصلبة. يمكن حساب تأثيرات استجابة المنحدر على القوة بالقصور الذاتي المؤثرة على كتلة الفشل المحتملة باستخدام تحليلات الإجهاد والتشوه الديناميكية (Chopra، 1966). باستخدام تحليل العناصر المحدودة الديناميكي (الشكل 10.16 a)، يتم دمج المكونات الأفقية للإجهادات الديناميكية المؤثرة على سطح الفشل المحتمل (الشكل 10.16 b) على سطح الفشل لإنتاج القوة الناتجة المتغيرة بمرور الوقت والتي تعمل على سطح الفشل المحتمل. يمكن بعد ذلك تقسيم هذه القوة الناتجة على كتلة التربة فوق سطح الفشل المحتمل لإنتاج متوسط تسارع كتلة الفشل المحتمل. على الرغم من أن الإجراء تم تطويره في الأصل للسدود، إلا أنه يمكن تطبيق المفهوم الأساسي على أي نوع من المنحدرات. يوفر سجل زمن التسارع المتوسط، والذي قد يكون بسعة أكبر أو أصغر من سجل زمن التسارع الأساسي (اعتمادًا على حركات الإدخال وخصائص التضخيم للمنحدر)، حركة الإدخال الأكثر واقعية لتحليل كتلة الانزلاق لكتلة الفشل المحتمل.
الشكل(10.12)
الشكل(10.13)
الشكل(10.14)
الشكل(10.15)
الشكل(10.16)
العوامل الأخرى المؤثرة على إزاحة المنحدر:
يعتمد تحليل كتلة الانزلاق القياسي على افتراض سلوك الإجهاد والانفعال تماما على سطح فشل مستو. قد تختلف شروط المنحدرات الفعلية عن هذه الافتراضات بعدة طرق. تعتمد قوة القص لبعض الترب على المعدل. نظرًا لأن إجهادات القص الناتجة عن الزلازل يتم تطبيقها بمعدلات مختلفة. يمكن أن تختلف قوة القص (وبالتالي تسارع الخضوع) مع مرور الوقت طوال الزلزال (على سبيل المثال، , Hungr and Morgenstern، 1984؛ Lemos et al، 1985). إن النظر في القوة المعتمدة على المعدل في تحليل كتلة الانزلاق معقد بسبب الاختلافات بين معدلات الانفعال في الحقل وفي الاختبارات المعملية المستخدمة لقياس القوة. اقترح Lemos and Coelh (1991) وTika-Vassilikos et al (1993) إجراءات لدمج قوى المجال المعتمدة على المعدل في تحليلات كتلة الانزلاق العددية. في الحقل، نادرًا ما تتصرف التربة كمواد لدنة تماما. بدلاً من ذلك، فإنها عادةً ما تظهر سلوك إجهاد-انفعال متصلب أو مخفف بالإجهاد (الشكل 10.17) بعد الخضوع. ستختلف تسارعات الخضوع للمنحدرات المكونة من تربة متصلبة أو مخففة بالإجهاد مع إزاحة المنحدر. وبالتالي، فإن التبديد الدائم للمنحدر في مواد التصلب بالإجهاد سيكون أصغر مما هو متوقع من خلال تحليل كتلة الانزلاق التقليدية؛ والعكس صحيح بالنسبة للتربة المخففة بالإجهاد. يعد تعديل تحليل كتلة الانزلاق للنظر في القوة المعتمدة على الإزاحة أمرًا مباشرًا إلى حد ما. تفشل العديد من المنحدرات بآليات تختلف عن آلية الفشل المستوية المفترضة في تحليل كتلة الانزلاق. بإهمال تأثيرات القوة المعتمدة على المعدل والإزاحة، فإن استقرار كتلة على مستوى سيكون هو نفسه قبل وبعد نبضة الإزاحة لأن هندسة الكتلة بالنسبة للمستوى لم تتغير. ومع ذلك، تميل حركة المنحدر على سطح فشل غير مستوٍ إلى تسطيح المنحدر، وبالتالي تقليل القوى الدافعة. نتيجة لذلك، يجب أن يزداد تسارع الخضوع بسبب التغيرات في هندسة التربة غير المستقرة. ومع ذلك، بالنسبة لمعظم المنحدرات، لا يصبح هذا التأثير مهمًا حتى تحدث إزاحات كبيرة.
تحليل مقدسي-سيد:
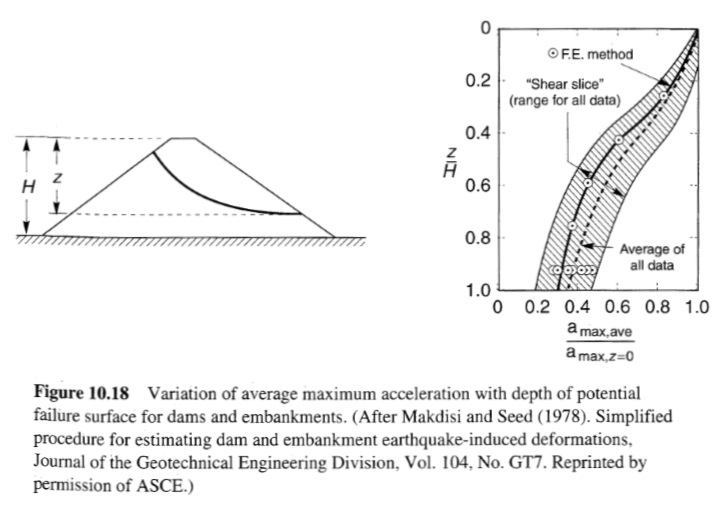
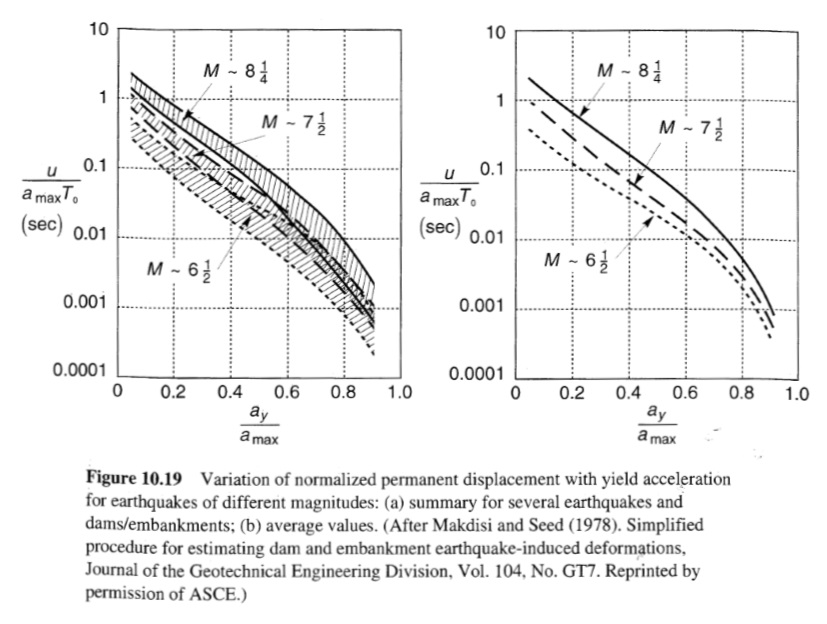
استخدم Makdisi and Seed (1978) متوسط التسارع المحسوب بواسطة إجراء Chopra (1966) وتحليلات كتلة الانزلاق لحساب التشوهات الدائمة الناجمة عن الزلازل للسدود الترابية والجسور. من خلال إجراء افتراضات مبسطة حول نتائج تحليل العناصر المحدودة الديناميكية وحزمة القص لمثل هذه الهياكل، تم تطوير إجراء مبسط للتنبؤ بالإزاحات الدائمة. في الإجراء المبسط، يتم حساب تسارع الخضوع لسطح فشل محتمل معين باستخدام قوة الخضوع الديناميكية [80٪ من القوة غير المصرفة] للتربة. إن الاستجابة الديناميكية لسد الداديم تُعزى إلى نسبة تسارع تختلف باختلاف عمق سطح الفشل المحتمل بالنسبة لارتفاع سد الداديم (الشكل 10.18). ومن خلال إخضاع العديد من السدود الحقيقية والافتراضية لعدة حركات أرضية فعلية وصناعية مُقاسة لتمثيل أحجام الزلازل المختلفة، قام مقديسي وسيد بحساب تغير الإزاحة الدائمة باستخدام ay/amax والحجم. وقد تم تقليل التشتت في الإزاحات المتوقعة عن طريق تطبيع الإزاحة فيما يتعلق بتسارع القاعدة الأقصى والفترة الأساسية لسد الداديم (لاحظ أن الإزاحة الطبيعية لها وحدات ثانية). ويتم التنبؤ بالإزاحات الدائمة بواسطة إجراء مقديسي-سيد باستخدام المخططات الموضحة في الشكل 10.19.
المثال الخامس:
افترض أن سطح الفشل الذي يمتد فوق الثلثين العلويين من السد الترابي له تسارع خضوع قدره 0.24g. ما هو قدر الإزاحة الدائمة التي قد تحدث إذا تعرضت قاعدة السد لحركة جيلروي رقم 1 (الصخرية).
الحل: تم تسجيل حركة جيلروي رقم 1 في زلزال لوما بريتا عام 1989 والذي بلغت قوته 7.1 درجة. وكان تسارع الذروة 0.442g. الفترة الأساسية للسد هي:
T0= 2π/19.2= 0.33 s
باستخدام الشكل 10.19b مع:
ay/amax = 0.24g/0.442g = 0.54 وM = 7.1، يكون متوسط الإزاحة الطبيعية حوالي 0.04 لذلك،
u = 0.04 amax T0 = 0.04(0.442g)(32.2 ft/s2/g)(0.33 sec) = 0.19 ft = 2.3 in
تُستخدم طريقة مكديسي-سيد المبسطة على نطاق واسع لتقدير الإزاحات الدائمة في السدود والجسور. ولأن الطريقة تعتمد على خصائص الاستجابة الديناميكية للسدود والجسور، فيجب تفسير نتائجها بحذر عند تطبيقها على أنواع أخرى من المنحدرات.
تحليل الإجهاد والتشوه:
تمامًا كما تُجرى عادةً تحليلات الإجهاد والتشوه لاستقرار المنحدر الساكن باستخدام تحليلات العناصر المحدودة الساكنة، تُجرى عادةً تحليلات الإجهاد والتشوه لاستقرار المنحدر الزلزالي باستخدام تحليلات العناصر المحدودة الديناميكية. في مثل هذه التحليلات يتم دمج الإجهادات الدائمة المستحثة زلزالياً في كل عنصر من عناصر شبكة العناصر المحدودة للحصول على التشوه الدائم للمنحدر. يمكن تقدير الإجهادات الدائمة داخل العناصر الفردية بطرق مختلفة. تقدر طرق جهد الإجهاد وتقليل الصلابة الإجهادات الدائمة باستخدام نتائج الاختبارات المعملية لتحديد “صلابة” التربة المعرضة لأحمال الزلازل. تستخدم طرق التحليل غير الخطي سلوك الإجهاد والانفعال غير المرن غير الخطي للتربة لحساب تطور الإجهادات الدائمة طوال الزلزال.
نهج جهد الإجهاد:
في تحقيقهم الرائد للانزلاقات التي حدثت في سدود سان فرناندو العلوية والسفلية أثناء زلزال سان فرناندو عام 1971، طور Seed et al (1973) إجراءً لتقدير تشوه المنحدر الناجم عن الزلزال من نتائج التحليلات الخطية أو التحليلات الخطية المكافئة. في هذا الإجراء يتم حساب إجهادات القص الدورية في كل عنصر من عناصر تحليل العناصر المحدودة الديناميكي. باستخدام نتائج الاختبارات المعملية الدورية، تُستخدم إجهادات القص الدورية المحسوبة للتنبؤ بإمكانية الانفعال، المعبر عنها بإجهاد قص، لكل عنصر. ثم يتم تقدير التشوهات على أنها حاصل ضرب متوسط إمكانية الانفعال على طول مقطع رأسي عبر المنحدر وارتفاع ذلك المقطع. تفترض الطريقة ضمناً أن الانفعالات التي تتطور في الحقل ستكون هي نفسها التي تتطور في عينة اختبار معملية محملة بشكل مماثل وأن أقصى إجهاد قص يعمل في الاتجاه الأفقي في جميع العناصر. وبالتالي، فإن نهج إمكانية الانفعال يقدر الإزاحات الأفقية فقط. من الواضح أن التحليلات القائمة على نهج إمكانية الانفعال تقريبية للغاية، ويجب دائمًا تفسير نتائجها مع وضع هذه الحقيقة في الاعتبار.
نهج تقليل الصلابة:
تم تطوير طريقة أخرى لتقدير إزاحة المنحدر الدائم بواسطة Lee (1974) وSerff et al (1976). في هذا النهج، تُستخدم إمكانات الانفعال المحسوبة لتقليل صلابة التربة كما هو موضح في الشكل 10.20. ثم يتم أخذ إزاحات المنحدر الناتجة عن الزلازل على أنها الفرق بين إزاحات النقطة العقدية من تحليلين ثابتين للعناصر المحدودة: أحدهما يستخدم وحدات القص الأولية والآخر يستخدم وحدات القص المخفضة. يمكن استخدام هذه التقنية مع النماذج الخطية أو غير الخطية. على عكس نهج جهد الانفعال، يمكن لنهج تقليل الصلابة تقدير الحركات الرأسية والأفقية. ومع ذلك، فهو إجراء تقريبي للغاية، ويخضع للعديد من القيود المفروضة على نهج جهد الانفعال. يمكن استخدام مبادئ طاقة العمل لتوفير إجراء أكثر جوهرية لتقليل الصلابة (Byrne، 1991؛ Byrne et al، 1992).
نهج التحليل غير الخطي:
يمكن أيضًا حساب تشوهات المنحدر الدائمة من خلال تحليلات العناصر المحدودة التي تستخدم نماذج التربة غير الخطية غير المرنة. تم تقديم الإجراءات الأساسية لتحليل العناصر المحدودة غير الخطي للهياكل الأرضية. تم تحليل الأداء الزلزالي للمنحدرات باستخدام تحليلات العناصر المحدودة ثنائية وثلاثية الأبعاد باستخدام كل من نماذج الإجهاد والانفعال الدورية (على سبيل المثال، Finn et al، 1986) والنماذج التأسيسية المتقدمة (على سبيل المثال، Prevost، 1981؛ Mizuno and Chen، 1982؛ Kawai، 1985؛ Daddazio et al، 1987). كان التطبيق الأكثر شيوعًا لهذه التقنيات، حتى الآن، هو تحليل السدود الترابية. يمكن العثور على أمثلة لمثل هذه التحليلات في Prevost et al (1985)، , Griffiths and Prevos (1988)، Finn (1990)، Elgamal et al (1990)، وSuccarieh et al (1991). إن دقة تحليلات العناصر المحدودة غير الخطية تعتمد في المقام الأول على دقة نماذج الإجهاد والانفعال أو النماذج التكوينية التي تستند إليها.
تحليل عدم الاستقرار الضعيف:
من خلال عملية توليد ضغط المسام و/أو الاضطراب الهيكلي، يمكن للإجهادات والانفعالات الناجمة عن الزلازل أن تقلل من قوة القص للتربة. يمكن أن تحدث عدم الاستقرار الضعيف عندما تنخفض القوة المنخفضة إلى ما دون إجهادات القص الثابتة والديناميكية المستحثة في المنحدر. عادة ما ترتبط عدم الاستقرار الضعيف بظواهر التميع ويمكن تقسيمها إلى فئتين رئيسيتين، الفشل المنخفض وفشل التشوه. تحدث حالات فشل التدفق عندما تصبح قوة القص المتاحة أصغر من إجهاد القص الساكن المطلوب للحفاظ على توازن المنحدر. وبالتالي، فإن حالات فشل التدفق مدفوعة فعليًا بإجهادات ساكنة. ويمكن أن تنتج تشوهات كبيرة جدًا تحدث بسرعة ودون سابق إنذار. تحدث حالات فشل التشوه عندما تنخفض قوة القص للتربة إلى النقطة التي يتجاوزها فيها مؤقتًا إجهاد القص الناجم عن الزلزال. ومثل حالات الفشل بالقصور الذاتي، تحدث حالات فشل التشوه كسلسلة من “نبضات” الإزاحة الدائمة التي تتوقف عند نهاية اهتزاز الزلزال. تتوفر إجراءات مختلفة لتحليل حالات فشل التدفق وحالات فشل التشوه.
تحليل فشل التدفق:
نظرًا لأنها تنطوي عادةً على انخفاض كبير في قوة التربة، فإن حالات فشل التدفق تنتج عادةً تشوهات كبيرة وأضرارًا شديدة. والخطوة الأولى في تحليلها هي عمومًا تحديد ما إذا كان سيحدث ذلك أم لا. لتقدير مدى الضرر الناتج عن حالات فشل التدفق، تم أيضًا تطوير إجراءات لتقدير تشوهات فشل التدفق. تحليل الاستقرار. يتم تقييم عدم استقرار انزلاق التدفق المحتمل بشكل شائع من خلال تحليلات استقرار المنحدر الثابت التقليدية باستخدام قوى التربة بناءً على ظروف نهاية الزلزال (Marcuson et al، 1990). في التحليل النموذجي، يتم حساب عوامل الأمان ضد التميع في جميع النقاط على سطح الفشل المحتمل أولاً. ثم يتم تعيين القوى المتبقية لتلك الأجزاء من سطح الفشل حيث يكون عامل الأمان ضد التميع أقل من 1. في المواقع حيث يكون عامل الأمان ضد التميع أكبر من 1، تعتمد قيم القوة على الإجهادات الفعالة في نهاية الزلزال (أي، مع مراعاة ضغوط المسام الناتجة أثناء الزلزال). باستخدام هذه القوى، يتم استخدام تحليلات استقرار المنحدر المتوازنة الحدية التقليدية لحساب عامل إجمالي للأمان ضد انزلاق التدفق. إذا كان عامل الأمان الإجمالي أقل من 1، فمن المتوقع حدوث انزلاق التدفق. يجب أن يؤخذ احتمال الفشل التدريجي في الاعتبار في تقييمات الاستقرار من هذا النوع – لا يتم أخذ إعادة توزيع الضغوط المشاركة في الفشل التدريجي في الاعتبار بشكل مباشر في تحليلات التوازن الحدي.
تحليل التشوهات:
إذا أشارت تحليلات الاستقرار إلى احتمال فشل التدفق، فيمكن تحديد مدى المنطقة المتأثرة بالفشل من تحليل تشوهات فشل التدفق. من خلال إهمال التشوهات الصغيرة التي تسبق تحفيز انزلاق التدفق، يمكن الحصول على تقديرات تقريبية لتشوهات انزلاق التدفق من الإجراءات القائمة على التوازن الحدي، وميكانيكا الموائع، وتحليلات الإجهاد والتشوه. يمكن استخدام إجراءات إجهاد المستوى البسيط وتوازن الحد لتقدير المسافة التي قد تتدفق بها التربة المسالة على منحدر لطيف (< 3 إلى 4 درجة) (Lucia et al، 1981). وبافتراض أن التربة المسالة ستستقر في النهاية على سطح خطي، يمكن تحديد هندسة ما بعد الفشل التي تلبي قيود التوازن والحجم. وبالإشارة إلى تدوين الشكل 10.21، يمكن تنفيذ الإجراء بالخطوات التالية:
- باستخدام الشكل 10.22 a، احسب قيم ارتفاع المنحدر في نهاية التدفق (عندما يصل عامل الأمان الثابت إلى 1.0) بناءً على اعتبارات القوة
HT,S= N0Sr/ϒ
باستخدام قيم مختلفة مفترضة لزاوية المنحدر، α. ارسم البيانات في شكل “منحنى قوة” كما في الشكل 10.22 b.
- بالنسبة للقيم المختلفة المفترضة لـ α، احسب ارتفاع المنحدر بعد التدفق بناءً على ظروف الحجم الثابت باستخدام
HT,V= (A12Hc2+A2Vf)1/2-A3Hc
حيث
A1=tan α/(tan α-tan β)
A2=2tan2 α/(tan α-tan β)
A3=tan β/(tan α-tan β)
Hc= 4Sr/ϒ
وVf هو الحجم المقدر للتربة المشاركة في انزلاق التدفق. ارسم البيانات الناتجة في شكل “منحنى حجم” كما في الشكل 10.22 b.
- تتقاطع منحنيات القوة والحجم حيث HT,S = HT,V. تلبي قيم Hstable وαstable,, الناتجة متطلبات القوة والحجم مع عامل أمان يساوي 1. يمكن بعد ذلك حساب المسافة الأفقية التي تغطيها شريحة التدفق على النحو التالي
L= (Hstable – Hc)/tan αstable
على الرغم من أن الإجراء يتضمن العديد من الافتراضات التبسيطية ويتطلب تقدير قوة التربة المسالة، إلا أنه يمكن أن يوفر على الأقل تقديرًا أوليًا للتشوهات المشاركة في بعض انزلاقات التدفق. لقد حفز السلوك المشابه للسوائل للتربة المسالة مناهج ميكانيكا الموائع لنمذجة سلوك انزلاق التدفق. وقد اتجهت أغلب هذه الأعمال نحو تدفقات الحطام (على سبيل المثال، Johnson، 1970؛Iverson and Denlinger، 1987) وانهيارات سدود المخلفات (على سبيل المثال، Jeyapalan et al، 1981). والنمذجة الريولوجية للتربة المسالة صعبة للغاية. ونموذج بينغهام ((strength = τy + ηpϒ، حيث τy وηp هما قوة خضوع بينغهام واللزوجة، على التوالي، وϒ هو معدل إجهاد القص) هو الأكثر استخدامًا (Johnson، 1970؛ Jeyapalan، 1980؛ O’Brien and Julien، 1988؛ Phillips and Davies، 1991)، على الرغم من أن قدرته على تمثيل الطبيعة الاحتكاكية للتربة المسالة محدودة (Iverson and LaHusen، 1993). وقد جعل تطوير التحليلات الديناميكية غير الخطية المتقدمة نهجًا بديلًا ممكنًا. على سبيل المثال، يمكن لبرنامج العناصر المحدودة TARA-3FL (Finn and Yogendrakumar، 1989) أن يقلل من قوة أي عنصر في المنحدر إلى القوة المتبقية في وقت بدء تميع العنصر. يقوم البرنامج بتحديث شبكة العناصر المحدودة بشكل دوري في كل خطوة زمنية للسماح بحساب التشوهات الكبيرة (الشكل 10.23). وصف Finn (1990) تطبيقه على سد سارديس في ولاية ميسيسيبي، حيث كان من المتوقع تسييل اللب وطبقة رقيقة من الطمي الطيني (الشكل 10.23). لا تشير التحليلات من هذا النوع إلى ما إذا كان انزلاق التدفق سيحدث فحسب، بل توفر أيضًا تقديرًا لتوزيع وحجم أي تشوهات ناتجة.
تحليل فشل التشوه:
على الرغم من أن فشل التشوه ينطوي عمومًا على تشوهات أصغر من فشل التدفق، إلا أنه قادر على التسبب في أضرار جسيمة. الانتشار الجانبي هو النوع الأكثر شيوعًا من فشل التشوه. في السنوات الأخيرة، طور عدد من الباحثين طرقًا لتقدير النزوح الدائم الناتج عن فشل التشوه. نظرًا لأن الآليات التي تنتج فشل التشوه معقدة للغاية، فإن إجراءات التنبؤ بالنزوح الناتج تجريبية إلى حد كبير في طبيعتها.
نهج حمادا وآخرون:
درس Hamada et al (1986) تأثيرات الظروف الجيوتقنية والطوبوغرافية على النزوح الدائم للأرض الملحوظ في الرمال المنتظمة ذات حجم الحبيبات المتوسط في زلازل نيغاتا عام 1964 (M = 7.5)، وسان فرناندو عام 1971 (M = 7.1)، ونيهونكاي-تشوبو عام 1983 (M = 7.7). وجد أن النزوح الدائم يتأثر بشدة بسمك الطبقة المسالة ومنحدرات سطح الأرض والحد السفلي للمنطقة المسالة. وجد أن النزوح الأرضي الأفقي الدائم، D، يختلف وفقًا للعلاقة التجريبية
D(m)= 0.75H1/2θ1/3
حيث H هو سمك الطبقة المسالة بالأمتار وθ هو الأكبر بين منحدر سطح الأرض أو منحدر الحد الأدنى للمنطقة المسالة كنسبة مئوية. بالنسبة لسجلات الحالات من الزلازل الثلاثة المدرجة، كان 80% من النزوح الملحوظ ضمن عامل 2. مثل جميع هذه الأساليب التجريبية، يجب تطبيقها بحذر عندما تختلف الظروف عن تلك التي تستند إليها.
نهج يود وبيركينز (مؤشر شدة التميع):
استنادًا إلى النزوحات الجانبية المرصودة من عدد من الحالات التاريخية في غرب الولايات المتحدة، عرّف Youd and Perkin (1987) مؤشر شدة التميع (LSI) بأنه “القيمة القصوى العامة (بالبوصة) للانتشارات الجانبية الناتجة عن السهول الفيضية النشطة الواسعة أو الدلتا أو مناطق أخرى من رواسب الأنهار المنحدرة بشكل لطيف في أواخر العصر الهولوسيني”. وكما هو محدد، يمثل مؤشر شدة التميع تقديرًا متحفظًا للنزوح الأرضي في منطقة معينة؛ ومن المتوقع أيضًا حدوث حالات فشل مع نزوح أصغر بمقدار 1 في المنطقة. أشار تحليل قاعدة بيانات تاريخ الحالة إلى أنه يمكن التنبؤ بمؤشر شدة التميع من خلال
Log (LSI) = -3.49-1.85 log R+0.98Mw<=100
حيث R هي المسافة الأفقية من مصدر الطاقة الزلزالية بالكيلومترات. يظهر التباين في مؤشر شدة التميع مع M وR في الشكل 10.24. يتم تقديم الأوصاف النوعية لطبيعة حالات فشل التشوه لقيم مختلفة لمؤشر شدة التميع في الجدول 10-5. إن اعتماد LSI على الحجم والمسافة يجعل من الممكن دمجه في تحليل المخاطر الزلزالية الاحتمالية. استخدم Youd and Perkins (1987) هذا النهج لإنتاج خرائط LSI الاحتمالية لجنوب كاليفورنيا.
نهج بايرن:
في نمذجة منحدر على هيئة قشرة من التربة السليمة ترتكز على طبقة من التربة المتميعة (الشكل 10.25)، استخدم Byrne (1991) مبادئ طاقة العمل مع نموذج مرن لدن تمامًا للتربة المسالة لتطوير تعبيرات لتقدير إزاحة المنحدر الدائمة. في هذا النهج، يتم الحصول على الإزاحة الدائمة، D، من
D3Sr/3(ϒlimTL)2-Dτst-1/2(mv02)=0 D<ϒlimTL
D= (3mv02+4SrϒlimTL)/6(Sr-τst) D>= ϒlimTL
حيث Sr، هي القوة المتبقية للتربة المسالة (الشكل 9.56)، ϒlim إجهاد القص الحدي، TL سمك الطبقة المسالة، τstمتوسط إجهاد القص المطلوب للتوازن الثابت (على سطح الفشل الذي يمر عبر منتصف عمق الطبقة المسالة)، m كتلة التربة فوق سطح الفشل، وv0، سرعة الكتلة في لحظة التميع. يتم تقديم القيم النموذجية لـ ϒlim، في الجدول 10-6.
وسّع Byrne et al (1992) هذا النهج لتحديد العوامل التي يجب أن يتم من خلالها تقليل الصلابة الأولية للتربة لتحليل العناصر المحدودة لفشل التشوه. وكانت التشوهات التي تنبأت بها هذه الطريقة متوافقة بشكل جيد مع تلك التي لوحظت في فشل سد سان فرناندو العلوي عام 1971 (الشكل 10.26).
المثال السادس:
يتكون الموقع المنحدر بلطف الموضح في الشكل(E10.6) من طبقة من الطين الطمي بسمك 2 متر فوق طبقة من الرمل المشبع السائب بسمك 4 أمتار. يحتوي الرمل على محتوى متوسط من المواد الدقيقة يبلغ حوالي 3% ومتوسط D50 = 0.22mm. تشير التحقيقات تحت السطحية إلى أن مقاومة SPT المصححة للرمل متوافقة تمامًا مع متوسط قيمة 11. قم بتقدير الإزاحة الدائمة للمنحدر عند تعرضه لهزات زلزالية كافية للتسبب في تميع الرمل.
الحل إجهاد القص الساكن في مركز الطبقة القابلة للتميع هو
τst= σv sin α = 2*1.92*9.81 + 2*1.85*9.81 = 5.2 kPa
من الجدول 10.6، ϒlim= 0.45 ومن الشكل 9.57، Su= 300 psf = 14.4 kPa. بافتراض أن المنحدر ليس له سرعة أولية (v0 = 0)، فإن:
D= 1.88m
نظرًا لأن هذه الإزاحة أقل من ϒlimTL,، فيجب تحديد الإزاحة الدائمة باستخدام المعادلة التكعيبية:
D = 1.87m
وبالتالي، فإن الإزاحة الدائمة المقدرة ستكون حوالي 1.9 م. لاحظ أن هذا التقدير يعتمد على متوسط قيمة القوة المتبقية للتربة المتميعة؛ وبالنظر إلى مدى عدم اليقين في تلك القوة (الشكل 9.58)، فإن الإزاحة الدائمة الفعلية يمكن أن تكون أصغر أو أكبر بشكل كبير.
نهج بازيار:
باستخدام تحليل كتلة الانزلاق لوصف الجوانب الأساسية لاستقرار المنحدر الزلزالي، طور Baziar et al (1992) تعبيرًا عامًا للإزاحة الجانبية الدائمة
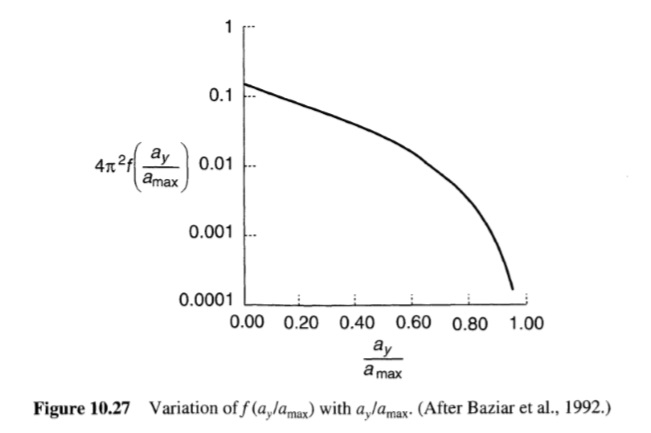
d = N(v2max/amax)f(ay/amax)
حيث N هو العدد المكافئ لدورات التحميل التوافقي، وvmax هي السرعة الأفقية الأعظمية، وamax هي التسارع الأفقي الأعظمي، وay هو تسارع الخضوع. تم الحصول على الدالة f(ay/amax) بافتراض التسارع التوافقي (الشكل 10.27).
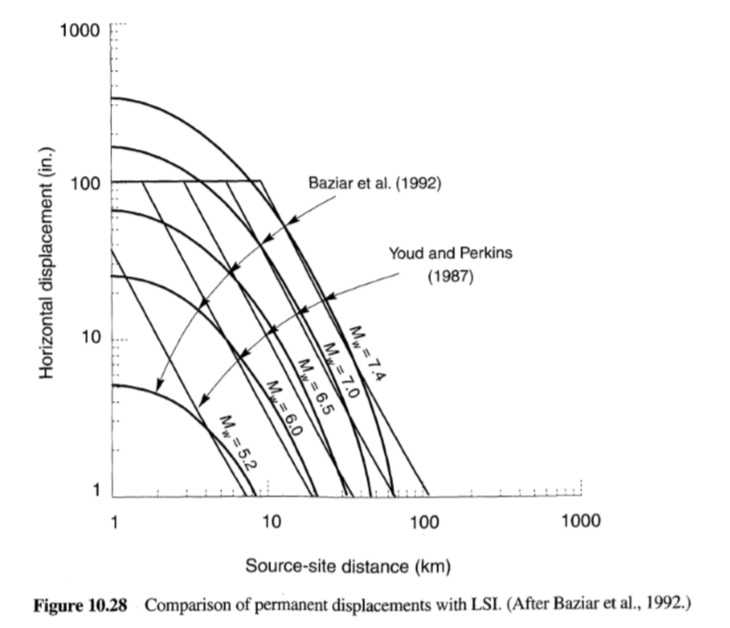
اقترحت نسبة الانحراف المعياري مقابل الحالات التاريخية من غرب الولايات المتحدة استخدام N = 2 لـ 5.0=<M<=7.7. من خلال افتراض تسارع العائد الممثل لتلك المرتبطة بقاعدة بيانات الحالات التاريخية الخاصة بـ Youd and Perkins (1987) ، تمكن Baziar et al (1992) من مقارنة النزوح المتوقع بواسطة المعادلة (10.23) بقيم LSI المقابلة. كما هو موضح في الشكل 10.28، فإن النهجين متسقان تمامًا عند مسافات أطول للمواقع، ولكن بدرجة أقل عند مسافات أقصر.
نهج يود وبارليت:
استخدم Bartlett and Youd (1992) قاعدة بيانات كبيرة لحالات الانتشار الجانبي لتطوير تعبيرات تجريبية تربط بين النزوح الأرضي الجانبي وعدد من معلمات المصدر والموقع. تضمنت قاعدة البيانات مواقع من غرب الولايات المتحدة واليابان على مسافات تصل إلى 90 كم من موقع المصدر تعرضت لزلزالين تتراوح قوتهما من 6.4 إلى 9.2 درجة. واستُخدمت تحليلات الانحدار لتحديد العوامل التي أثرت بقوة على النزوح الجانبي للأرض، بحيث يمكن أن يستند النموذج التجريبي إلى تلك العوامل. وتم تطوير نموذجين تجريبيين: نموذج الوجه الحر للمواقع القريبة من الضفاف شديدة الانحدار ونموذج المنحدر الأرضي للمواقع ذات المنحدرات الخفيفة. بالنسبة للمواقع ذات الوجه الحر، يمكن الحصول على الإزاحات من:
log DH =- 16.3658 + 1.1782Mw – 0.9275logR – 0.0133R + 0.6572logW + 0.3483logT15 + 4.5720log (100 – F15) – 0.9224(D50)15
حيث DH هو الإزاحة الجانبية المقدرة للأرض بالأمتار، Mw، قدر العزم، R المسافة الأفقية من مصدر الطاقة الزلزالية بالكيلومتر، W نسبة ارتفاع الوجه الحر إلى المسافة الأفقية بين قاعدة الوجه الحر ونقطة الاهتمام (الشكل 10.29)، T15 السُمك التراكمي للطبقات الحبيبية المشبعة مع ((N1)60<15 بالأمتار، F15 متوسط محتوى الغرامات للطبقات الحبيبية التي تضم T15، كنسبة مئوية، و15(D50)، متوسط حجم الحبيبات المتوسط للطبقات الحبيبية التي تضم T15 بالملليمتر. بالنسبة للمواقع ذات المنحدرات اللطيفة، يتنبأ نموذج المنحدر الأرضي بـ:
logDH = – 16.3658 + 1.1782Mw – 0.9275logR – 0.0133R + 0.4293logS + 0.3483logT15 + 4.572log(100-F15) – 0.9224(D50)15
حيث S هو المنحدر الأرضي كنسبة مئوية (الشكل 10.29). أظهر تطبيق هذه المعادلات على قاعدة البيانات أن 90% من النزوحات الملحوظة كانت ضمن عامل 2 من القيم المتوقعة. يوضح الجدول 10-7 نطاقات معلمات الإدخال التي يتم التحقق من نتائجها المتوقعة من خلال ملاحظات التاريخ.
المثال السابع:
قم بتقدير الإزاحة الدائمة للمنحدر الموصوف في المثال السادس بسبب حدوث زلزالين بقوة M = 6.5 وM = 7.5 على مسافة (موقع المصدر الأفقي) 30 كم. الحل من الوصف الوارد في المثال 10.6، فإن نموذج المنحدر الأرضي الذي وضعه بارتليت ويود هو الأكثر ملاءمة. المعلمات ذات الصلة هي:
S=4, T15 = 4, F15 = 3, (D50)15 = 0.22
(ثم يمكن تقدير الإزاحة الدائمة بسبب زلزال Mw = 6.5 على النحو التالي
10logD = – 16.3658 + (1.1782)(6.5) – 0.9275 log(30) – 0.0133(30) + 0.4293 log(4) + 0.3483 log(4) + 4.5270 log(100 – 3) – 0.9224(0.22) = -1.217
D = 10-1.217 = 0.061m = 6.1 cm
بالنسبة لزلزال Mw = 7.5،
D = 0.91m = 91cm
مناقشة: قدمت الأقسام السابقة مجموعة متنوعة من الطرق لتقدير النزوحات الدائمة الناتجة عن فشل التشوه. معظم هذه الطرق تجريبية للغاية، وكلها تنتج تقديرات تقريبية فقط للنزوحات الدائمة. تعتمد قابلية تطبيق كل طريقة على موقع معين على التشابه بين الظروف في ذلك الموقع وتلك المقابلة لقواعد البيانات التي تم تطوير الطريقة منها.

الشكل(10.17)
الشكل(10.18)
الشكل(10.19)

الشكل(10.20)
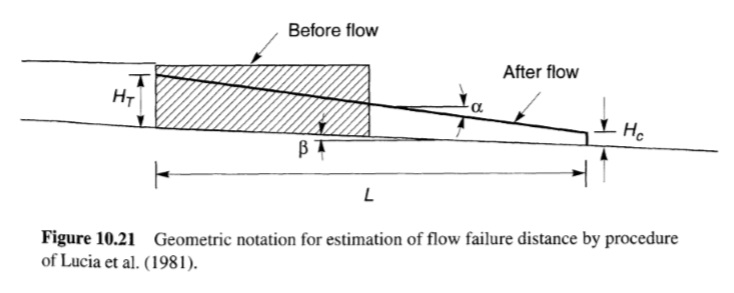
الشكل(10.21)
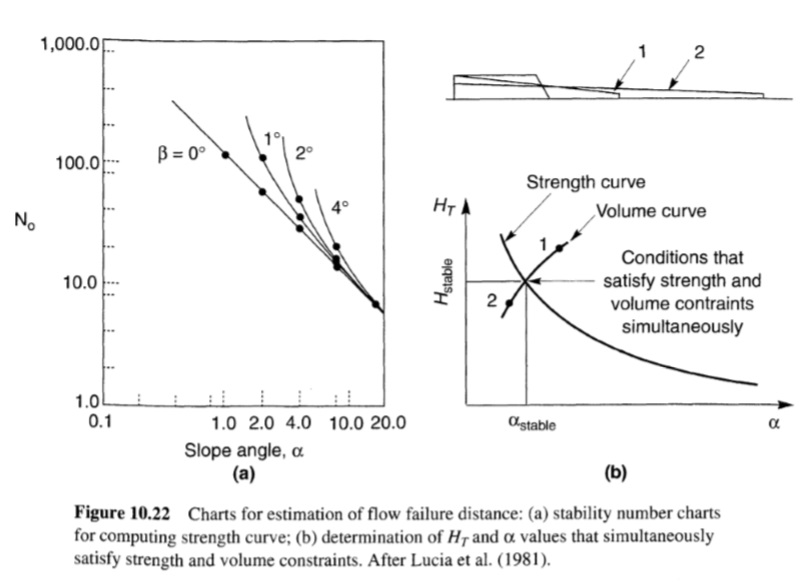
الشكل(10.22)
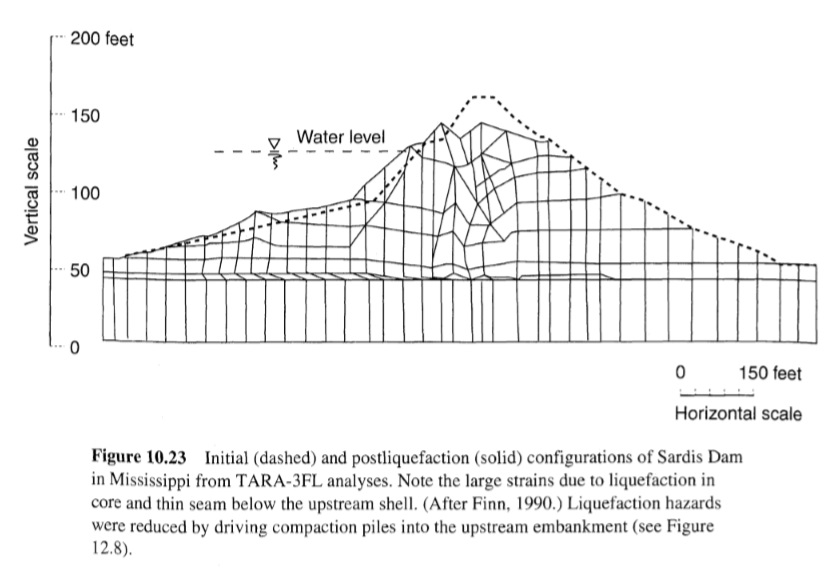
الشكل(10.23)

الشكل(10.24)

الجدول(10.5)

الشكل(10.25)
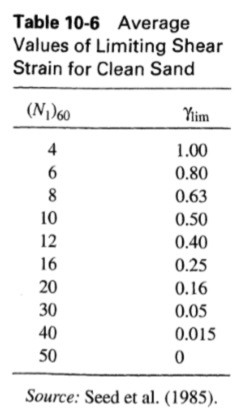
الجدول(10.6)
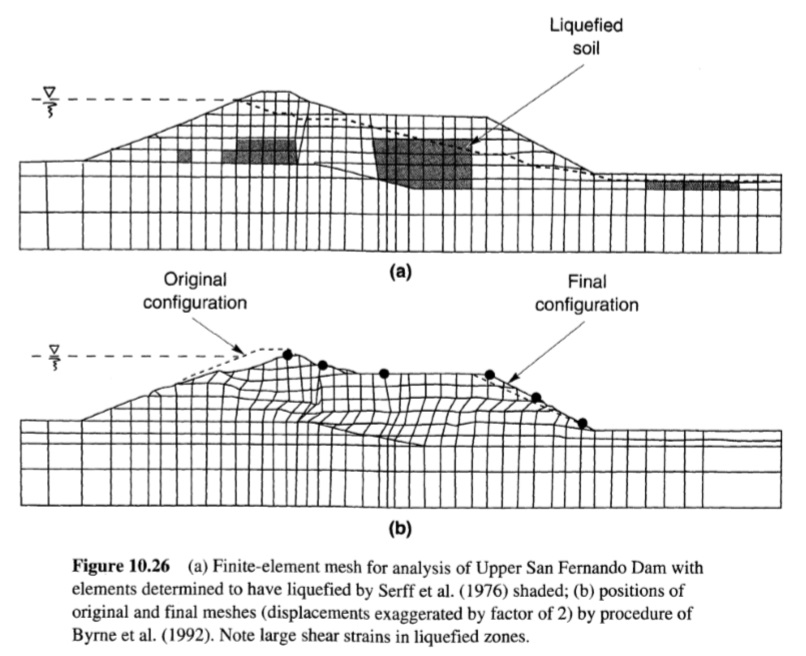
الشكل(10.26)

الشكل(E10.6)
الشكل(10.27)
الشكل(10.28)

الشكل(10.29)
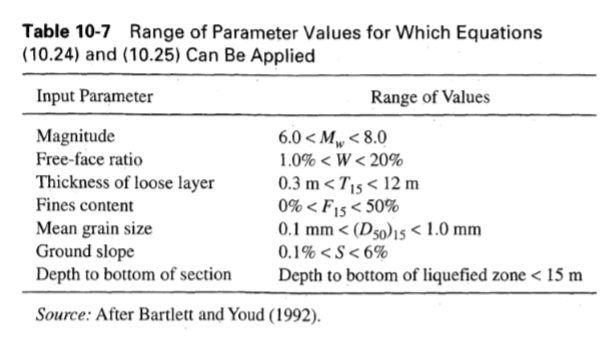
الجدول(10.7)
الملخص:
- تاريخيًا، كانت الانهيارات الأرضية الناجمة عن الزلازل من بين أكثر المخاطر الزلزالية ضررًا. وتتأثر خصائصها بالظروف الجيولوجية والهيدرولوجية والطوبوغرافية والمناخية والعوامل الجوية واستخدام الأراضي. ويمكن تصنيف الانهيارات الأرضية على أساس نوع المادة ونوع الحركة ودرجة الاضطراب الداخلي ومحتوى الماء والسرعة والعمق. وعادةً ما تنقسم الانهيارات الأرضية الناجمة عن الزلازل إلى ثلاث فئات رئيسية: الانهيارات الأرضية المتقطعة والانهيارات الأرضية المتماسكة والانتشارات والتدفقات الجانبية.
- يسمح تحليل البيانات التاريخية بتقدير الحد الأدنى لشدة الزلزال المطلوبة لإنتاج أنواع مختلفة من الانهيارات الأرضية والحد الأقصى للمسافة التي يمكن توقع حدوث الانهيارات الأرضية إليها في الزلازل ذات الشدة المختلفة.
- لا يشكل تحليل استقرار المنحدر سوى جزء واحد من التقييم الشامل لاستقرار المنحدر. وقبل التحليل، يجب الحصول على معلومات مفصلة عن الخصائص الجيولوجية والهيدرولوجية والطوبوغرافية والهندسية والمادية. إن دقة التحليل لن تكون جيدة إلا بقدر دقة هذه المعلومات.
- تمثل إجهادات القص الديناميكية الناتجة عن اهتزازات الزلزال مصدرًا للتحميل وقد تؤثر أيضًا على سلوك القوة والإجهاد والانفعال لمواد المنحدر. يمكن تجميع عدم استقرار المنحدر الزلزالي في فئتين على أساس أي من هذه التأثيرات هو السائد في منحدر معين. عدم الاستقرار بالقصور الذاتي هو تلك التي تظل فيها قوة القص للتربة ثابتة بشكل أساسي وتنتج تشوهات المنحدر عن تجاوزها المؤقت للإجهادات الزلزالية الديناميكية. تحدث عدم الاستقرار الضعيف عندما يعمل الزلزال على إضعاف التربة بدرجة كافية بحيث لا يمكنها البقاء مستقرة تحت الضغوط الناجمة عن الزلزال.
- يتم تحليل عدم الاستقرار بالقصور الذاتي بشكل شائع من خلال تحليلات كتلة الانزلاق أو تشوه الإجهاد. كما يتم استخدام نهج Makdisi-Seed بشكل متكرر، استنادًا إلى نتائج تحليلات كتلة الانزلاق.
- تمثل التحليلات شبه الثابتة تأثيرات الزلزال من خلال تطبيق تسارعات أفقية و/أو رأسية ثابتة على كتلة تربة غير مستقرة محتملة. تعمل القوى بالقصور الذاتي التي يسببها هذا التسارع شبه الثابت على زيادة القوى الدافعة وقد تقلل من القوى المقاومة المؤثرة على التربة. لا تصلح التحليلات شبه الثابتة للتربة التي تتراكم فيها ضغوط مسام كبيرة أو تظهر تدهورًا في القوة يزيد عن 15% بسبب اهتزاز الزلزال. يتم التعبير عن الاستقرار من حيث عامل الأمان شبه الثابت المحسوب بإجراءات التوازن الحدي. يتطلب اختيار تسارع شبه ثابت مناسب عناية كبيرة: عادةً ما يتم استخدام قيم أصغر بكثير من تسارع الذروة للكتلة المنزلقة.
- يُعرف التسارع شبه الثابت المطلوب لجلب المنحدر إلى نقطة الفشل الأولي باسم تسارع الخضوع. إذا تجاوزت التسارعات الناجمة عن الزلزال في المنحدر تسارع الخضوع مؤقتًا، فإن التربة غير المستقرة ستتسارع مؤقتًا بالنسبة للمادة الموجودة تحتها. يمكن استخدام تحليلات كتلة الانزلاق لحساب مقدار الإزاحة التي تحدث. يعتمد الإزاحة الكلية على المقدار الذي يتم به تجاوز تسارع الخضوع (دالة على سعة حركة الأرض)، والوقت الذي يتم خلاله تجاوز تسارع الخضوع (دالة على محتوى التردد لحركة الأرض)، وعدد المرات التي يتم فيها تجاوز تسارع الخضوع (دالة على مدة حركة الأرض). ونظرًا للطبيعة المتغيرة للغاية لخصائص حركة الأرض، يمكن أن تكون الإزاحات المحسوبة متغيرة تمامًا.
- تعتمد طريقة مقدسي-سيد على تحليل الكتل المنزلقة للسدود الترابية والجسور. وبمعرفة الفترة الأساسية لاهتزاز الجسور الترابية وتسارع الخضوع للمنحدر، يمكن استخدام مخططات بسيطة لتقدير النزوح الدائم الناجم عن الزلازل.
- تم استخدام تحليلات الإجهاد والتشوه لتقدير التشوهات الدائمة الناجمة عن عدم الاستقرار بالقصور الذاتي. تسمح أساليب تقليل الجهد الانفعالي والصلابة بتقدير التشوهات الدائمة من تحليلات بسيطة نسبيًا؛ تقديراتها تقريبية للغاية. على الرغم من زيادة الجهد الحسابي بشكل كبير، يمكن تحليل التشوهات الدائمة بشكل أكثر صرامة باستخدام تقنيات العناصر المحدودة غير الخطية. مع تحسن دقة النماذج التأسيسية للتربة، من المرجح أن يزداد استخدام تحليلات العناصر المحدودة غير الخطية.
- تحدث حالات عدم الاستقرار الضعيفة عندما تقلل الإجهادات والانفعالات الناجمة عن الزلزال من قوة القص للتربة داخل المنحدر. اعتمادًا على ما إذا كانت القوة المخفضة أكبر من أو أقل من الضغوط المطلوبة للحفاظ على التوازن الثابت، يمكن تصنيف عدم الاستقرار الضعيف على أنه فشل في التدفق أو فشل في التشوه.
- يتم تقييم عدم استقرار فشل التدفق عادةً من خلال تحليل التوازن الحدي. يتم تطبيق القوى المتبقية على تلك الأجزاء من سطح الفشل التي تمر عبر التربة المسالة. يشير عامل الأمان الأقل من 1 إلى أن فشل التدفق محتمل. يمكن استخدام تحليلات توازن الحد البسيط جنبًا إلى جنب مع قيود الحجم الثابت لتقدير المسافة التي تنتقل بها المواد في فشل التدفق. كما تم استخدام نماذج ميكانيكا الموائع لتقدير تشوهات فشل التدفق. كما تم تطوير تحليلات ديناميكية غير خطية تسمح بإضعاف العناصر المسالة والإجهادات الكبيرة.
- يتم التعبير عن تأثيرات فشل التشوه عادةً من حيث تشوهات المنحدر. تم تطوير عدد من الأساليب، بدءًا من الأساليب التجريبية البحتة إلى الأساليب القائمة على نموذج كتلة الانزلاق، لتقدير التشوهات الناتجة عن فشل التشوه.
مسائل:
10.1 يتقاطع المنحدر الموضح أدناه مع درزتين من مادة طينية بسمك 6 بوصات. يمكن وصف مواد المنحدر السليمة بالمعلمات، c = 2500 psf، 0 = φ، ϒ = 130 psf. تُظهر الدرزات الطينية c = 750 psf، φ = 0، ϒ = 120 psf. احسب الحد الأدنى لعامل الأمان الساكن للمنحدر.
10.2 احسب الحد الأدنى لعامل الأمان شبه الساكن لمنحدر المسألة 10.1 بافتراض معامل شبه ساكن يساوي 0.1g.
10.3 احسب تسارع الخضوع لمنحدر المسألة 10.1.
10.4 باستخدام الحسابات اليدوية أو مخططات استقرار المنحدر. أو برنامج كمبيوتر لتحليل استقرار المنحدر، حدد سطح الفشل الدائري الحرج للمنحدر الموضح أدناه. بالنظر إلى سطح الفشل هذا فقط، احسب تسارع الخضوع للمنحدر.
10.5 يخضع المنحدر الموضح في المسألة 10.4 للتاريخ الزمني لتسارع القمة الموضح في الشكل(P10.5). احسب الإزاحة الدائمة للمنحدر.
10.6 تم تحديد أن أحد الجسور القائمة له تسارع خضوع يبلغ 0.2g. باستخدام علاقات Ambraseys وMenu، قدر احتمالية أن يتسبب زلزال ينتج تسارع ذروة يبلغ 0.3g في إزاحة دائمة للمنحدر أكبر من 2.5 سم.
10.7 تم تحديد أن المنحدر في التربة المتماسكة له تسارع خضوع يبلغ 0.17g. بافتراض أن Neq = 10 واستخدام علاقة Yegian et al، احسب القيمة المتوقعة لإزاحة المنحدر الدائم إذا تعرض المنحدر لـ (أ) حركة جيلروي رقم 1 (الصخر)، و (ب) حركة جيلروي رقم 2 (التربة).
10.8 باستخدام علاقة جيبسون، كرر المسألة 10.7. ثم احسب إزاحة المنحدر الدائم التي سيكون احتمال تجاوزها 5 في المائة لكل حركة أرضية.
10.9 تم حساب التردد الأساسي في المثال 7.6 على أنه 3.1 هرتز. تشير تحليلات استقرار المنحدر شبه الثابت إلى تسارع خضوع قدره 0.21g. استخدم إجراء مقدسي – سيد لتقدير الإزاحة الدائمة للسد في زلزال بقوة M = 7 ينتج عنه تسارع ذروة قدره 0.28g.
10.10 يتكون المنحدر الموضح أدناه من 5 أمتار من الرمل النظيف السائب فوق حصى طينية كثيفة للغاية مع منسوب مياه جوفية يبلغ 2 متر تحت سطح الأرض. باستخدام نهج بايرن، قم بتقدير الإزاحات الدائمة التي قد تحدث إذا تعرض المنحدر لهزات زلزالية قوية بما يكفي لبدء تسييل الرمل السائب.
10.11 باستخدام نهج بزيار وآخرين، قم بتقدير الإزاحات الدائمة التي كانت ستحدث في منحدرات متطابقة مع تسارع خضوع يبلغ 0.26g إذا تعرضت لـ (أ) حركة جيلروي رقم 1 (الصخور)، و (ب) حركة جيلروي رقم 2 (التربة). علق على فائدة تسارع الذروة كمؤشر وحيد لتشوهات المنحدر المحتملة.
10.12 يتكون المنحدر الموضح أدناه من رمل طيني سائب فوق طين صلب. قم بتقدير الإزاحة الجانبية المنتشرة التي قد تتطور إذا حدث زلزال بقوة M = 7.3 على مسافة (من مصدر الزلزال) 40 كم.

الشكل(P10.1)

الشكل(P10.4)

الشكل(P10.5)

الشكل(P10.10)
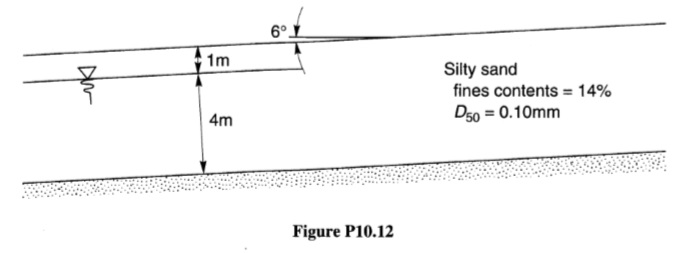
الشكل(P10.12)
LI, T. (1990). “Landslide management in mountain areas of China,” Occasional Paper 15, Interna- tional Centre for Integrated Mountain Development, Kathmandu, Nepal, 50 pp.
YOUD, T.L. (1978). “Major cause of earthquake damage is ground failure,” Civil Engineering, ASCE, Vol. 48, No. 4, pp. 47-51.
WILSON, R. C. AKD KEEFER, D. K. (1985) “Predicting areal limits of earthquake-induced landsliding,” in Evaluating Earthquake Hazards in the Los Angeles Region, Ziony, J. I., ed., U. S. Geological Survey, Reston, Virginia, Professional Paper 1360, 3 17-345.
KOBAYASHI, Y. (1981). “Causes of fatalities in recent earthquakes in Japan,” Journal of Disaster Science, Vol. 3, pp. 15-22.
CLOSE, U. AND MCCORMICK, E. (1922). “Where the mountains walked,” National Geographic, Vol. 41, No. 5, pp. 445-464.
KEEFER, D.K. (1984). “Landslides caused by earthquakes,” Geologic Society of America Bulletin, Vol. 95, No. 2, pp. 406-421.
VARNES, D.J. (1978). ”Slope movement types and processes,” in Landslides: Analysis and Control, Transportation Research Board Special Report 176, National Academy of Sciences, Washington, D.C., pp. 12-33.
DUNCAN, J.M. (1992). “State-of-the-art: static stability and deformation analysis,” in R.B. Seed and R.W. Boulanger, eds., Proceedings, Specialty Conference on Stability and Performance of Slopes and Embankments, 11, ASCE, New York, Vol. 1, pp. 222-266
NATIONAL RESEARCH COUNCIL (1976). Landslides, analysis and control, Special Report 176, R.L. Schuster and R.J. Krizek, eds., Transportation Research Board, Washington, D.C., 234 pp.
CHOWDHURY, R.N. (1978). Slope analysis, Elsevier, New York, 423 pp.
HUANG, Y.H. (1983). Stability Analysis of Earth Slopes, Van Nostrand Reinhold, New York, 305 pp.
TAYLOR, D.W. (1948). Fundamentals of Soil Mechanics, Wiley. New York, 700 pp.
PERLOFF, W.H. ARD BARON, W. (1976). Soil Mechanics, Ronald Press, New York.
LAMBE, T.W. AND WHITMAY, R.V. (1969). Soil Mechanics, Wiley, New York.
FELLENIUS, W. (1927). Erdstatische Berechnutzgen mit Reibung und Kohasion, Ernst, Berlin.
BISHOPA, .W. (1955). “The use of the slip circle in the stability analysis of slopes,” Geotechnique.
MORGENSTERN, N.R. AND PRICE, V.E. (1965). “The analysis of the stability of general slip surfaces,” Geotechnique, Vol. 15, No. 1, pp. 79-93.
SPEXCER, E. (1967). “A method of analysis of the stability of embankments assuming parallel inter- slice forces,” Geotechnique. Vol 17, No. 1, pp. 11-26.
JANBU, N. (1968). “Slope stability computations,” Soil Mechanics and Foundation Engineering Report, Technical University of Norway, Trondheim.
KONDNER, R.L. (1963). “Hyperbolic stress-strain response: cohesive soils,” Journal of the Soil Mechanics and Foعndations Division, ASCE, Vol89, NO. SM1, pp. 115.
KONDNER, R.L. AND ZELASKO, J.S. (1963). “A hyperbolic stress-strain formulation of sands,” Proceedings, 2nd Pan American Conference on Soil Mechanics and Foundation Engineering, Brazil, Vol. 1, p. 281.
DUNCAN, J.M. AND CHANG, C.Y. (1970). “Nonlinear analysis of stress and strain in soils,” Journal of the Soil Mechanics and Foundations Division, ASCE, Vol. 96, No. SM5, pp. 1629-1653.
DUNCAN, J.M., BYRNE, P.M., WONG, K.S., AND MABRY, P. (1980). “Strength, stress-strain, and bulk modulus parameters for finite element analysis of stresses and movements in soil masses,” Report UCB/GT/80-01, University of California, Berkeley.
TERZAGHI, K. (1950). Mechanisms of landslides, Engineering Geology (Berkey) Volume, Geological Society of America.
MARCUSONW, W.F. (1981). “Moderator’s report for session on ‘Earth dams and stability of slopes under dynamic loads’ ,” Proceedings, International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics, St. Louis, Missouri, Vol. 3, p. 1175.
DAKOULASP,. AND GAZETAS, G. (1986). “Seismic lateral vibration of embankment dams in semi- cylindrical valleys,” Earthquake Engineering and Structural Dynamics, Vol. 13, No. 1, pp. 19-40.
SEED,H .B. AND MARTIN, G.R. (1966). “The seismic coefficient in earth dam design,” Journal of the Soil Mechanics and Foundations Division, ASCE, Vol. 92, No. SM3, pp. 25-58.
SEED, H.B. (1979). Considerations in the earthquake-resistant design of earth and rockfill dams, Geotechnique, Vol. 29, No. 3, pp. 215-263.
HYNES-GRIFFINM, .E. AND FRANKLIN, A.G. (1984). “Rationalizing the seismic coefficient method,” Miscellaneous Paper GL-84-13, U.S. Army Corps of Engineers Waterways Experiment Station, Vicksburg, Mississippi, 21 pp.
SEED, H.B., LEE, K.L., AND IDRISS, I.M. (1969). “Analysis of Sheffield Dam failure,” Journal of the Soil Mechanics and Foundations Division, ASCE, Vol. 95, No. SM6, pp. 1453-1490.
SEED, H.B., LEE, K.L., IDRISS, I.M., AND MAKDISFI,. I. (1975). “The slides in the San Fernando Dams during the earthquake of February 9, 1971,” Journal of the Geotechnical Engineering Division, ASCE, Vol. 101, No. GT7, pp. 65 1-688.
MARCUSON, W.F., 111, BALLARD, R.F., JR., AND LEDBETTER, R.H. (1979). “Liquefaction failure of tailings dams resulting from the Near Izu Oshima earthquake, 14 and 15 January, 1978,” Proceedings, 6th Pan American Conference on Soil Mechanics and Foundation Engineering, Lima, Peru.
NEWMARK, N. (1965). “Effects of earthquakes on dams and embankments,” Geotechnique, Vol. 15, NO. 2, pp. 139-160.
SARMA, S.K. (1975). “Seismic stability of earth dams and embankments,” Geotechnique, Vol. 25, pp. 743-761.
YEGIAN, M.K., MARCIANO, E. AND GHAHRAMAN, V.G. (1991). “Earthquake-induced permanent deformations: probabilistic approach,” Journal of Geotechnical Engineering, ASCE, Vol. 117, No. 1, pp. 35-50.
FRANKLINA,. G. AND CHANG, F.K. (1977). Permanent displacements of earth embankments by New- mark sliding block analysis, Report 5, Miscellaneous Paper ,571-17, U.S. Army Corps of Engineers Waterways Experiment Station, Vicksburg, Mississippi.
MAKDISI, F.I. AND SEED, H.B. (1978). “Simplified procedure for estimating dam and embankment earthquake-induced deformations,” Journal of the Geotechnical Engineering Division, ASCE, Vol. 104, No. GT7, pp. 849-867.
AMBRASEYS, N.N. AND MENU, J.M. (1988). “Earthquake-induced ground displacements,” Earth- quake Engineering and Structural Dynamics, Vol. 16, pp. 985-1006.
YEGIAN, M.K., MARCIANO, E.A., AND GHARAMAN, V.G. (1988). “Integrated seismic risk analysis for earth dams,” Report 88-15, Northeastern University, Boston.
CONSTAKTIKOU, M. AND GAZETASG, . (1984). “Probabilistic seismic sliding deformations of earth dams and slopes,” Proceedings, 4th ASCE Specialty Conference on Probabilistic Mechanics and Structural Reliability, pp. 318-321.
LIN, J.S. AND WHITMAN, R.V. (1986). “Earthquake induced displacements of sliding blocks,” Journal of Geotechnical Engineering, ASCE, Vol. 112, NO. 1, pp. 44-59.
JIBSON, R. (1994). “Predicting earthquake-induced landslide displacements using Newmark’s sliding block analysis,” Transportation Research Record 1411, Transportation Research Board, Washington, D.C., pp. 9-17.
WILSON, R. C. AKD KEEFER, D. K. (1985) “Predicting areal limits of earthquake-induced landsliding,” in Evaluating Earthquake Hazards in the Los Angeles Region, Ziony, J. I., ed., U. S. Geological Survey, Reston, Virginia, Professional Paper 1360, 317-345.
CHOPRA, A.K. (1966). “Earthquake effects on dams,” Ph.D. dissertation, University of California, Berkeley.
HUNGR, O. AND MORGEXSTERN; N.R. (1984). “High velocity ring shear tests on sand,” Geotechnique, Vol. 34, No. 3, pp. 415-421.
LEMOS, L.J.L., SKEMPTOK, A.W., AND VAUGHAN, P.R. (1985). “Earthquake loading of shear surfaces in slopes,” Proceedings, 1 lth International Conference on Soil Mechanics and Foundation Engineering, San Francisco, Vol. 4, pp. 1955-1958.
LEMOS, L.J.L. AND COELHO, P.A.L.F. (1991). Displacements of slopes under earthquake loading, Proceedings, 2nd International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics, St. Louis, Missouri, Vol. 2, pp. 1051-1056.
TIKA-VASSILIKOS, T.E., SARMA, S.K., AND AMBRASEYS, N. (1993). “Seismic displacements on shear surfaces in cohesive soils,” Earthquake Engineering and Structural Dynamics, Vol. 22, pp. 709-721.
MAKDISI, F.I. AND SEED, H.B. (1978). “Simplified procedure for estimating dam and embankment earthquake-induced deformations,” Journal of the Geotechnical Engineering Division, ASCE, Vol. 104, No. GT7, pp. 849-867.
SEED, H.B., LEE, K.L., IDRISS, I.M., AND MAKDISI, R. (1973). “Analysis of the slides in the San Fernando dams during the earthquake of Feb. 9,1971,” Report No. EERC 73-2, Earthquake Engineering Research Center, University of California, Berkeley, 150 pp.
LEE, K.L. (1974). Seismic permanent deformations in earth dams, Report No. UCLA-ENG-7497, School of Engineering and Applied Science, University of California at LOS Angeles.
SERFF. N., SEED: H.B., MAKDISI, F.I., AND CHANG, C.-Y. (1976). “Earthquake-induced deformations of earth dams,” Report EERC 76-4, Earthquake Engineering Research Center, University of California, Berkeley, 140 pp.
BYRNE, P.M. (1991). “A model for predicting liquefaction induced displacement,” Proceedings, 2nd International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics, St. Louis, Missouri, Vol. 2, pp. 1027-1035.
BYRNE, P.M., JITNO, H., AND SALGADO, R. (1992). “Earthquake-induced displacements of soil-structures systems,” Proceedings, 10th World Conference on Earthquake Engineering, Madrid, Vol. 3, pp. 1407-1412.
FINN, W.D.L., YOGENDRAKUMAR, M., YOSHIDA, M.. AND YOSHIDAN, . (1986). TAM-3: A Program to Compute the Response of2-D Embankments and Soil-Structure Interaction Systems to Seismic Loadslidings, Department of Civil Engineering, University of British Columbia, Vancouver.
PREVOST, J.H. (1981). DYNAFLOW: A Nonlinear Transient Finite Element Analysis Program, Department of Civil Engineering, Princeton University, Princeton, New Jersey.
MIZUNO, E. AND CHEN, W.F. (1982). “Plasticity models for seismic analysis of slopes,” Report CE- STR-82-2, School of Civil Engineering. Purdue University, West Lafayette, Indiana.
KAWAI, T. (1985). DIANA – Dynamic interaction approach and non-linear analysis, Summary Report, Science University of Tokyo.
DADDAZIOR, .P., ETTOUNEY, M.M., AND SANDLER, I.S. (1987). “Nonlinear dynamic slope stability analysis,” Journal of Geotechnical Engineering, ASCE, Vol. 113, No. 4, pp. 285-298.
PREVOST, J.H., ABDEL-GHAFFARA,. M., AND LACY,S .J. (1985). “Nonlinear dynamic analysis of earth dams: a comparative study,” Journal of Geotechnical Engineering, ASCE, Vol. 11 1, No. 2, pp. 882-897.
GRIFFITHSD,. V. AND PREVOST, J.H. (1988). “Two- and three-dimensional finite element analyses of the Long Valley Dam,” Technical Report NCEER-88-0015, National Center for Earthquake Engineering Research, Buffalo, New York.
FINN,W .D.L. (1990). “Analysis of post-liquefaction deformations in soil structures,” Proceedings, H. Bolton Seed Memorial Symposium, University of California, Berkeley, Vol. 2, pp. 291-312.
ELGAMALA, .M., SCOTT, R.F., SUCCARIEHM,. F., AND YAN, L.P. (1990). “La Villita Dam response during five earthquake including permanent deformation,” Journal of Geotechnical Engineering, ASCE, Vol. 11 6, No. 10, pp. 1443- 1462.
SUCCARIEH, M.F., YAN,L ., AND ELGAMAL, A.M. (1991). “Modelling of observed deformation at La Villita dam,” Proceedings, 2nd International Conference on Recent Advances in Geotechnical Earth- 1 quake Engineering and Soil Dynamics, St. Louis, Missouri, Vol. 2, pp. 1079-1086.
MARCUSON, W.F. 111, HYNES, M.E., AND FRANKLINA, .G. (1990). Evaluation and use of residual strength in seismic safety analysis of embankments, Earthquake Spectra, Vol. 6, NO. 3, pp. 529-572.
LUCIA, P.C., DUNCAN, J.M., AND SEED, H.B. (1981). “Summary of research on case histories of flow failures of mine tailings impoundments, “Information Circular 8857, Technology Transfer Workshop on Mine Waste Disposal Techniques, U.S. Bureau of Mines, Denver, Colorado, pp. 46-53.
JOHNSON, A.M. (1970). Physical Processes in Geology, Freeman, Cooper, San Francisco, 577 pp.
IVERSON, R.M. AND DENLINGER, R.P. (1987). “The physics of debris flows: a conceptual assessment,” in R.L. Beschta, T. Blinn, G.E. Grant, G.G. Ice, and F.J. Swanson, eds. Proceedings, Erosion and Sedimentation in the Pacific Rim, International Association of Hydrological Science, Corvallis, Oregon, pp. 155-165.
JEYAPALAN, J.K., DUNCANJ,. M., AND SEED,H .B. (1981). “Summary of research on flow failures of mine tailings impoundments,” Information Circular 8857, Technology Transfer Workshop on Mine Waste Disposal Techniques, U.S. Bureau of Mines, Denver, Colorado, pp. 54-63.
JEYAPALAN, J.K. (1980). “Analyses of flow failures of mine tailings impoundments,” Ph.D. Dissertation, University of California, Berkeley, 298 pp.
O’BRIEN, J.S. AND JULIEN, P.Y. (1988). “Laboratory analysis of mudflow properties,” Journal of Hydraulic Engineering, ASCE, Vol. 114, pp. 877-887.
PHILLIPS, C.J. AND DAVIES, T.R. (1991). “Determining rheological parameters of debris flow material,” Geomorphology, Vol. 4, pp. 101-110.
IVERSON, R.M. AND LAHUSEN, R.G. (1993). “Friction in debris flows: Inferences from large-scale flume experiments,” Proceedings, Hydraulics Engineering ’93, ASCE, San Francisco, pp. 1604-1609.
FINN, W.D.L. AND YOGEKDRAKUMAR, M. (1989). TARA-3FL – Program for analysis of liquefaction induced flow deformations, Department of Civil Engineering, University of British Columbia, Vancouver, British Columbia.
FINN,W .D.L. (1990). “Analysis of post-liquefaction deformations in soil structures,” Proceedings, H. Bolton Seed Memorial Symposium, University of California, Berkeley, Vol. 2, pp. 291-312.
HAMADA, M., YASUDA, S., ISOYAMA, R., AI\D EMOTO, K. (1986). “Study on liquefaction induced per- manent ground displacements,” Report for the Association for the Development of Earthquake Prediction.
YOUD, T.L. AND PERKINS, D.M. (1987). “Mapping of Liquefaction Severity Index,” Journal of Geo- technical Engineering, ASCE, Vol. 113, No. 11, pp. 1374-1392.
BAZIAR, M.H., DOBRY, R., AND ELGAMEL, A.W.M. (1992). “Engineering evaluation of permanent ground deformations due to seismically-induced liquefaction,” Technical Report NCEER-92-0007. National Center for Earthquake Engineering Research, State University of New York, Buffalo.
BARTLETT, S.F. AND YOUD, T.L. (1992). “Empirical analysis of horizontal ground displacement generated by liquefaction-induced lateral spread,” Technical Report NCEER-92-0021, National Center for Earthquake Engineering Research, Buffalo, New York.
